Guitar Strings
A guitar string has a number of frequencies at which it will
naturally vibrate. These natural frequencies are known as the harmonics of the
guitar string. As mentioned earlier, the natural frequency at which an object vibrates
at depends upon the tension of the string, the linear density of the string and
the length of the string. Each of these natural frequencies or harmonics is
associated with a standing wave pattern. The specifics of the patterns and
their formation were discussed in Lesson 4. For now, we will merely summarize the
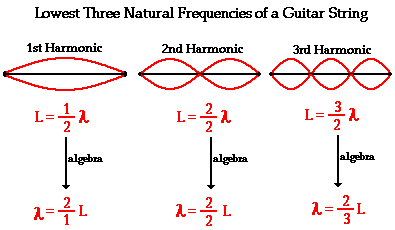
results of that discussion. The graphic below depicts the standing wave
patterns for the lowest three harmonics or frequencies of a guitar string.
Problem-Solving
Scheme
The wavelength of the standing wave for any given harmonic is
related to the length of the string (and vice versa). If the length of a guitar
string is known, the wavelength associated with each of the harmonic
frequencies can be found. Thus, the length-wavelength relationships and the wave equation (speed = frequency
* wavelength) can be combined to perform calculations predicting the length of
string required to produce a given natural frequency. And conversely,
calculations can be performed to predict the natural frequencies produced by a
known length of string. Each of these calculations requires knowledge of the
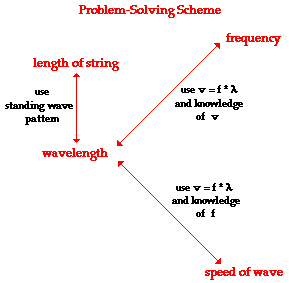
speed of a wave in a string. The graphic below depicts the relationships
between the key variables in such calculations. These relationships will be
used to assist in the solution to problems involving standing waves in musical
instruments.
To demonstrate the use of the above problem-solving scheme,
consider the following problem and its detailed solution.
Example Problem #1
The speed of waves in a particular
guitar string is 425 m/s. Determine the fundamental frequency (1st harmonic)
of the string if its length is 76.5 cm. |
The solution to the problem begins by first identifying known
information, listing the desired quantity, and constructing a diagram of the
situation.
|
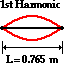
Given: v = 425 m/s L = 76.5 cm = 0.765 m |
Find: f1 = ?? |
Diagram:
|
The problem statement asks us to determine the frequency (f)
value. From the graphic above, the only means of finding the frequency is to use the
wave equation (speed=frequency • wavelength) and knowledge of the speed and
wavelength. The speed is given, but wavelength is not known. If the wavelength
could be found, then the frequency could be easily calculated. In this problem
(and any problem), knowledge of the length and the harmonic number allows one
to determine the wavelength of the wave. For the first harmonic, the wavelength
is twice the length. This relationship is derived from the diagram of the
standing wave pattern (and was explained in detail in Lesson 4). This
relationship, which works only for the first harmonic of a guitar string, is
used to calculate the wavelength for this standing wave.
Wavelength = 2 • Length
Wavelength = 2 • 0.765 m
Wavelength = 1.53 m
Now that wavelength is known, it can be combined with the
given value of the speed to calculate the frequency of the first harmonic for
this given string. This calculation is shown below.
speed = frequency • wavelength
frequency = speed /
wavelength
frequency = (425 m/s) /
(1.53 m)
frequency = 278 Hz
Most problems can be solved in a similar manner. It is always
wise to take the extra time needed to set the problem up; take the time to
write down the given information and the requested information and to draw a
meaningful diagram. These preparatory steps become more important as problems
become more difficult.
Seldom in physics are two problems identical. The tendency to
treat every problem the same way is perhaps one of the quickest paths to
failure. It is important to combine good problem-solving skills (part of which
involves the discipline to set the problem up) with a solid grasp of the
relationships among variables. Avoid the tendency to memorize approaches to
different types of problems. To further your understanding of these
relationships and the use of the above
problem-solving scheme, examine the following problem and its solution.
Example Problem #2
Determine the length of guitar string
required to produce a fundamental frequency (1st harmonic) of 256 Hz. The
speed of waves in a particular guitar string is known to be 405 m/s. |
The solution to the problem begins by first identifying known
information, listing the desired quantity, and constructing a diagram of the
situation.
|
Given: v = 405 m/s f1 = 256 Hz |
Find: L = ?? |
Diagram:
|
The problem statement asks us to determine the length of the
guitar string. From the graphic above, the only means of finding the
length of the string is from knowledge of the wavelength. But the wavelength is
not known. However, the frequency and speed are given, so one can use the wave
equation (speed = frequency • wavelength) and knowledge of the speed and
frequency to determine the wavelength. This calculation is shown below.
speed = frequency • wavelength
wavelength = speed
/ frequency
wavelength = (405 m/s)
/ (256 Hz)
wavelength = 1.58 m
Now that the wavelength is found, the length of the guitar
string can be calculated. For the first harmonic, the length is one-half the
wavelength. This relationship is derived from the diagram of the standing wave
pattern (and was explained in detail in Lesson 4). It may also be
evident to you by looking at the standing wave diagram drawn above. This
relationship between wavelength and length, which works only for the first
harmonic of a guitar string, is used to calculate the wavelength for this
standing wave pattern.
Length = (1/2) • Wavelength
Length = (1/2) • Wavelength
Length = 0.791 m
If you have successfully followed the logic in the above two
example problems, take a try at the following practice problems. As you
proceed, be sure to be mindful of the numerical relationships involved in such
problems. And if necessary, refer to the graphic above.
Check Your Understanding
1. A guitar string with a length of 80.0 cm is plucked. The
speed of a wave in the string is 400 m/sec. Calculate the
frequency of the first, second, and third harmonics.
Answers: f1 = 250 Hz; f2 = 500 Hz; f3 = 750 Hz
Given: L = 0.80 m
v = 400 m/s
The strategy for solving for the frequencies of the first three
harmonics will be to first find the frequency of the first harmonic. The
frequencies of other harmonics are multiples of the first harmonic. The
frequency of the first harmonic can be calculated from the given speed value
and the wavelength. The wavelength is not given but can be calculated from the
length of the string. For the first harmonic, the wavelength is twice the
length of the string (see Tutorial page).
Let
λ = wavelength.
λ = 2• L = 2
• (0.80 m) = 1.6 m
Now rearrange the wave equation v = f • λ to solve for
frequency.
f1 =
v / λ = (400 m/s) / (1.6 m) = 250 Hz
The frequencies of the various harmonics are whole-number
multiples of the frequency of the first harmonic. Each harmonic frequency (fn) is given by the
equation fn = n • f1 where n is
the harmonic number and f1 is the frequency of the first harmonic.
Second
harmonic: f2 = 500 Hz
Third harmonic: f3 = 750 Hz
2. A pitch of Middle D (first harmonic = 294 Hz) is sounded
out by a vibrating guitar string. The length of the string is 70.0 cm.
Calculate the speed of the standing wave in the guitar string.
Answer: v = 412 m/s
Given: L = 0.70 m
f = 294 Hz (1st)
The strategy for solving for the speed of sound will involve
using the wave equation v = f •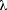 
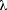where is the
wavelength of the wave. The frequency is stated but the wavelength must be
calculated from the given value of the length of the string. For the first
harmonic, the wavelength is twice the length of the string (see Tutorial page).
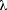= 2 • L = 2 • (0.70
m) = 1.4 m
Now substitute into the wave equation to solve for the speed of
the wave.
v = f • 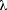= (294 Hz) •
(1.4 m)
v = 412 m/s
3. A frequency of the first harmonic is 587 Hz (pitch of D5)
is sounded out by a vibrating guitar string. The speed of the wave is 600
m/sec. Find the length of the string.
Answer:
L = 0.51 m
Given:
f = 587 Hz
v
= 600 m/s
The
length of a guitar string is related mathematically to the wavelength of the
wave which resonates within it. Thus the strategy for solving for length will
be to first determine the wavelength of the wave using the wave equation and
the knowledge of the frequency and the speed. The wave equation states that v =
f • λ where λ is the wavelength of the wave.
Rearranging this equation and substituting allows one to determine the
wavelength.
λ = v / f =
(600 m/s) / (587 Hz) = 1.02 m
For
the first harmonic, the length of the string is one-half the wavelength of the
wave (see Tutorial page). Thus, the following calculation can be performed:
L = 0.5 • 1.02 m = 0.51 m