Fundamental Frequency and Harmonics

Previously in Lesson 4, it was mentioned that when an object is forced into resonance vibrations at one of its natural frequencies, it vibrates in a manner such that a standing wave pattern is formed within the object. Whether it is a guitar sting, a Chladni plate, or the air column enclosed within a trombone, the vibrating medium vibrates in such a way that a standing wave pattern results. Each natural frequency that an object or instrument produces has its own characteristic vibrational mode or standing wave pattern. These patterns are only created within the object or instrument at specific frequencies of vibration; these frequencies are known as harmonic frequencies, or merely harmonics. At any frequency other than a harmonic frequency, the resulting disturbance of the medium is irregular and non-repeating. For musical instruments and other objects that vibrate in regular and periodic fashion, the harmonic frequencies are related to each other by simple whole number ratios. This is part of the reason why such instruments sound pleasant. We will see in this part of Lesson 4 why these whole number ratios exist for a musical instrument.

Recognizing the Length-Wavelength Relationship

First, consider a guitar string vibrating at its natural frequency or harmonic frequency. Because the ends of the string are attached and fixed in place to the guitar's structure (the bridge at one end and the frets at the other), the ends of the string are unable to move. Subsequently, these ends become nodes - points of no displacement. In between these two nodes at the end of the string, there must be at least one antinode. The most fundamental harmonic for a guitar string is the harmonic associated with a standing wave having only one antinode positioned between the two nodes on the end of the 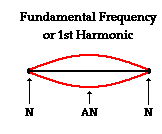string. This would be the harmonic with the longest wavelength and the lowest frequency. The lowest frequency produced by any particular instrument is known as the fundamental frequency. The fundamental frequency is also called the first harmonic of the instrument. The diagram at the right shows the first harmonic of a guitar string. If you analyze the wave pattern in the guitar string for this harmonic, you will notice that there is not quite one complete wave within the pattern. A complete wave starts at the rest position, rises to a crest, returns to rest, drops to a trough, and finally returns to the rest position before starting its next cycle. (Caution: the use of the words crest and trough to describe the pattern are only used to help identify the length of a repeating wave cycle. A standing wave pattern is not actually a wave, but rather a pattern of a wave. Thus, it does not consist of crests and troughs, but rather nodes and antinodes. The pattern is the result of the interference of two waves to produce these nodes and antinodes.) In this pattern, there is only one-half of a wave within the length of the string. 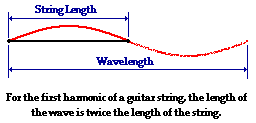This is the case for the first harmonic or fundamental frequency of a guitar string. The diagram below depicts this length-wavelength relationship for the fundamental frequency of a guitar string.

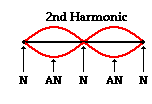The second harmonic of a guitar string is produced by adding one more node between the ends of the guitar string. And of course, if a node is added to the pattern, then an antinode must be added as well in order to maintain an alternating pattern of nodes and antinodes. In order to create a regular and repeating pattern, that node must be located midway between the ends of the guitar string. This additional node gives the second harmonic a total of three nodes and two antinodes. The standing wave pattern for the second harmonic is shown at the right. A careful investigation of the pattern reveals that there is exactly one full wave within the length of the guitar string. For this reason, the length of the string is equal to the length of the wave.

The third harmonic of a guitar string is produced by adding two nodes between the ends of the guitar string. And of course, if two nodes are added to the pattern, then two antinodes must be added as well in order to maintain an alternating pattern of nodes and antinodes. In order to create a regular and repeating pattern for this harmonic, the two additional nodes must be evenly spaced between the ends of the guitar string. This places them at the one-third mark and the two-thirds mark along the string. These additional nodes give the third harmonic a total of four nodes and three antinodes. The standing wave pattern for the third harmonic is shown at the right. A careful investigation of the pattern reveals that there is more than one full wave within the length of the guitar string. In fact, there are three-halves of a wave within the length of the guitar string. 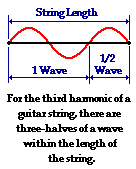For this reason, the length of the string is equal to three-halves the length of the wave. The diagram below depicts this length-wavelength relationship for the fundamental frequency of a guitar string.

After a discussion of the first three harmonics, a pattern can be recognized. Each harmonic results in an additional node and antinode, and an additional half of a wave within the string. If the number of waves in a string is known, then an equation relating the wavelength of the standing wave pattern to the length of the string can be algebraically derived.

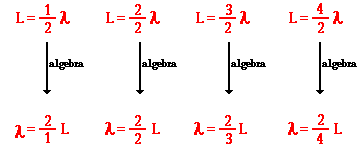
This information is summarized in the table below.

Harmonic #	# of Waves in String	# of Nodes	# of Anti- nodes	Length- Wavelength Relationship
1	1/2	2	1	Wavelength = (2/1)*L
2	1 or 2/2	3	2	Wavelength = (2/2)*L
3	3/2	4	3	Wavelength = (2/3)*L
4	2 or 4/2	5	4	Wavelength = (2/4)*L
5	5/2	6	5	Wavelength = (2/5)*L

The above discussion develops the mathematical relationship between the length of a guitar string and the wavelength of the standing wave patterns for the various harmonics that could be established within the string. Now these length-wavelength relationships will be used to develop relationships for the ratio of the wavelengths and the ratio of the frequencies for the various harmonics played by a string instrument (such as a guitar string).

Determining the Harmonic Frequencies

Consider an 80-cm long guitar string that has a fundamental frequency (1st harmonic) of 400 Hz. For the first harmonic, the wavelength of the wave pattern would be two times the length of the string (see table above); thus, the wavelength is 160 cm or 1.60 m. The speed of the standing wave can now be determined from the wavelength and the frequency. The speed of the standing wave is

speed = frequency • wavelength

speed = 400 Hz • 1.6 m

speed = 640 m/s

This speed of 640 m/s corresponds to the speed of any wave within the guitar string. Since the speed of a wave is dependent upon the properties of the medium (and not upon the properties of the wave), every wave will have the same speed in this string regardless of its frequency and its wavelength. So the standing wave pattern associated with the second harmonic, third harmonic, fourth harmonic, etc. will also have this speed of 640 m/s. A change in frequency or wavelength will NOT cause a change in speed.

Using the table above, the wavelength of the second harmonic (denoted by the symbol λ₂) would be 0.8 m (the same as the length of the string). The speed of the standing wave pattern (denoted by the symbol v) is still 640 m/s. Now the wave equation can be used to determine the frequency of the second harmonic (denoted by the symbol f₂).

speed = frequency • wavelength

frequency = speed/wavelength

f₂ = v / λ₂

f₂ = (640 m/s)/(0.8 m)

f₂ = 800 Hz

This same process can be repeated for the third harmonic. Using the table above, the wavelength of the third harmonic (denoted by the symbol λ₃) would be 0.533 m (two-thirds of the length of the string). The speed of the standing wave pattern (denoted by the symbol v) is still 640 m/s. Now the wave equation can be used to determine the frequency of the third harmonic (denoted by the symbol f₃).

speed = frequency • wavelength

frequency = speed/wavelength

f₃ = v / λ₃

f₃ = (640 m/s)/(0.533 m)

f₃ = 1200 Hz

Now if you have been following along, you will have recognized a pattern. The frequency of the second harmonic is two times the frequency of the first harmonic. The frequency of the third harmonic is three times the frequency of the first harmonic. The frequency of the nth harmonic (where n represents the harmonic # of any of the harmonics) is n times the frequency of the first harmonic. In equation form, this can be written as

f_n = n • f₁

The inverse of this pattern exists for the wavelength values of the various harmonics. The wavelength of the second harmonic is one-half (1/2) the wavelength of the first harmonic. The wavelength of the third harmonic is one-third (1/3) the wavelength of the first harmonic. And the wavelength of the nth harmonic is one-nth (1/n) the wavelength of the first harmonic. In equation form, this can be written as

λ_n = (1/n) • λ₁

These relationships between wavelengths and frequencies of the various harmonics for a guitar string are summarized in the table below.

Harmonic #	Frequency (Hz)	Wavelength (m)	Speed (m/s)	fn / f1	λn / λ1
1	400	1.60	640	1	1/1
2	800	0.800	640	2	1/2
3	1200	0.533	640	3	1/3
4	1600	0.400	640	4	1/4
5	2000	0.320	640	5	1/5
n	n * 400	(2/n)*(0.800)	640	n	1/n

The table above demonstrates that the individual frequencies in the set of natural frequencies produced by a guitar string are related to each other by whole number ratios. For instance, the first and second harmonics have a 2:1 frequency ratio; the second and the third harmonics have a 3:2 frequency ratio; the third and the fourth harmonics have a 4:3 frequency ratio; and the fifth and the fourth harmonic have a 5:4 frequency ratio. When the guitar is played, the string, sound box and surrounding air vibrate at a set of frequencies to produce a wave with a mixture of harmonics. The exact composition of that mixture determines the timbre or quality of sound that is heard. If there is only a single harmonic sounding out in the mixture (in which case, it wouldn't be a mixture), then the sound is rather pure-sounding. On the other hand, if there are a variety of frequencies sounding out in the mixture, then the timbre of the sound is rather rich in quality.

Check Your Understanding

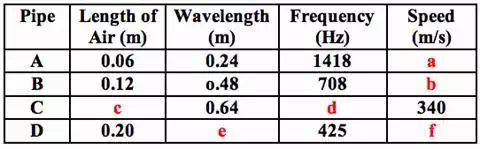
1. Anna Litical cuts short sections of PVC pipe into different lengths and mounts them in putty on the table. The PVC pipes form closed-end air columns that sound out at different frequencies when she blows over the top of them. The actual frequency of vibration is inversely proportional to the wavelength of the sound; and thus, the frequency of vibration is inversely proportional to the length of air inside the tubes. Express your understanding of this resonance phenomenon by filling in the following table.

See Answer

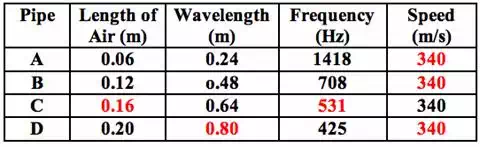
The speed of wave is not dependent upon wave properties such as wavelength and frequency. Thus, the speed of the sound wave is 340 m/s for each of the four pipes.

For Pipe C, the frequency can be determined from knowledge of the speed and the wavelength using the wave equation: v = f • λ where λ is the wavelength. First, rearrange the equation. Then substitute and solve as shown below.

f = v / λ = (340 m/s) / (0.64 m) = 531 Hz

For all four pipes, the length of the air column inside the pipe is one-fourth the wavelength of the wave. This is evident when looking at the length - wavelength relationships for Pipes A and B. Put in equation form: L = 0.25 • λ where λ is the wavelength. For Pipe C:

L = 0.25 • λ = 0.25 • (0.64 m) = 0.16 m

For Pipe D, the determination of the wavelength demands that the L = 0.25 • λ equation be rearranged.

λ = 4 • L = 4 • 0.20 m = 0.80 m

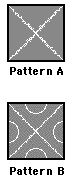2. In a rare moment of artistic brilliance, a Physics teacher pulls out his violin bow and strokes a square metal plate to produce vibrations within the plate. Often times, he places salt upon the plate and observes the standing wave patterns established in the plate as it vibrates. Amazingly, the salt is aligned along the locations of the plate that are not vibrating and far from the locations of maximum vibration. The two most common standing wave patterns are illustrated at the right. Compare the wavelength of pattern A to the wavelength of pattern B. Suppose that the fundamental frequency of vibration is nearly 1200 Hz. Estimate the frequency of vibration of the plate when it vibrates in the second, third and fourth harmonics.

See Answer

The frequencies of the various harmonics are multiples of the frequency of the first harmonic. Each harmonic frequency (f_n) is given by the equation f_n = n • f₁ where n is the harmonic number and f₁ is the frequency of the first harmonic.

f₂ = 2 • f₁ = 2400 Hz

f₃ = 3 • f₁ = 3600 Hz

f₄ = 4 • f₁ = 4800 Hz

3. When a tennis racket strikes a tennis ball, the racket begins to vibrate. There is a set of selected frequencies at which the racket will tend to vibrate. Each frequency in the set is characterized by a particular standing wave pattern. The diagrams below show the three of the more common standing wave patterns for the vibrations of a tennis racket.

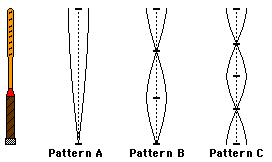
a. Compare the wavelength of pattern A to the wavelength of pattern B. Make your comparison both qualitative and quantitative. Repeat for pattern C.

See Answer

The wavelength of A is bigger than B which is bigger than C.

In A, there is 1/4-th of a wave in the racket. In B, there is 3/4-ths of a wave in the racket. In C, there is 4/4-ths of a wave in the racket. Thus, the wave in Pattern A is 3 times the length of Wave in Pattern B and 4 times the length of wave in Pattern C.

b. Compare the frequency of pattern A to the frequency of pattern B. Make your comparison both qualitative and quantitative. Repeat for pattern C.

See Answer

The frequency of C is bigger than B which is bigger than A.

In A, there is 1/4-th of a wave in the racket. In B, there is 3/4-ths of a wave in the racket. In C, there is 4/4-ths of a wave in the racket. Frequency and wavelength are inversely related. The longer the wavelength, the lower the frequency. Thus, wave B is 3 times the frequency of Wave A and wave C is 4 times the frequency of wave A.

c. When the racket vibrates as in pattern A, its frequency of vibration is approximately 30 Hz. Determine the frequency of vibration of the racket when it vibrates as in pattern B and pattern C.

See Answer

Following from the reasoning to the previous answer in part b of this question, wave B must have a frequency of 90 Hz and wave C must have a frequency of 120 Hz.