Properties of a Wave
The
Anatomy of a Wave
A transverse wave is a wave
in which the particles of the medium are displaced in a direction perpendicular
to the direction of energy transport. A transverse wave can be created in a
rope if the rope is stretched out horizontally and the end is vibrated
back-and-forth in a vertical direction. If a snapshot of such a transverse wave
could be taken so as to freeze the shape
of the rope in time, then it would look like the following diagram.
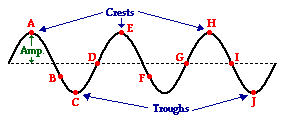
The dashed line drawn through the center of
the diagram represents the equilibrium or rest position of the
string. This is the position that the string would assume if there were no
disturbance moving through it. Once a disturbance is introduced into the
string, the particles of the string begin to vibrate upwards and downwards. At
any given moment in time, a particle on the medium could be above or below the
rest position. Points A, E and H on the diagram represent the crests of this
wave. The crest of a wave is the point on the medium that
exhibits the maximum amount of positive or upward displacement from the rest
position. Points C and J on the diagram represent the troughs of this wave. The trough of a wave
is the point on the medium that exhibits the maximum amount of negative or
downward displacement from the rest position.
The wave shown above can be described by a
variety of properties. One such property is amplitude. The amplitude of a wave
refers to the maximum amount of displacement of a particle on the medium from
its rest position. In a sense, the amplitude is the distance from rest
to crest. Similarly, the amplitude can be measured from
the rest position to the trough position. In the diagram above, the amplitude
could be measured as the distance of a line segment that is perpendicular to
the rest position and extends vertically upward from the rest position to point
A.
The wavelength is another property of a wave
that is portrayed in the diagram above. The wavelength of a wave
is simply the length of one complete wave cycle. If you were to trace your
finger across the wave in the diagram above, you would notice that your finger
repeats its path. A wave is a repeating pattern. It repeats itself in a
periodic and regular fashion over both time and space. And the length of one
such spatial repetition (known as a wave cycle) is the
wavelength. The wavelength can be measured as the distance from crest to crest
or from trough to trough. In fact, the wavelength of a wave can be measured as
the distance from a point on a wave to the corresponding point on the next
cycle of the wave. In the diagram above, the wavelength is the horizontal
distance from A to E, or the horizontal distance from B to F, or the horizontal
distance from D to G, or the horizontal distance from E to H. Any one of these
distance measurements would suffice in determining the wavelength of this wave.
A longitudinal wave is a wave
in which the particles of the medium are displaced in a direction parallel to
the direction of energy transport. A longitudinal wave can be created in a
slinky if the slinky is stretched out horizontally and the end coil is vibrated
back-and-forth in a horizontal direction. If a snapshot of such a longitudinal
wave could be taken so as to freeze the shape
of the slinky in time, then it would look like the following diagram.
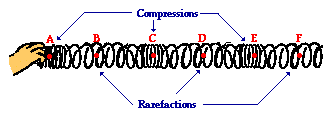
Because the coils of the slinky are vibrating longitudinally,
there are regions where they become pressed together and other regions where
they are spread apart. A region where the coils are pressed together in a small
amount of space is known as a compression. A compression is a point
on a medium through which a longitudinal wave is traveling that has the maximum
density. A region where the coils are spread apart, thus maximizing the
distance between coils, is known as a rarefaction. A rarefaction is a point
on a medium through which a longitudinal wave is traveling that has the minimum
density. Points A, C and E on the diagram above represent compressions and
points B, D, and F represent rarefactions. While a transverse wave has an
alternating pattern of crests and troughs, a longitudinal wave has an
alternating pattern of compressions and rarefactions.
As discussed above, the wavelength of a wave
is the length of one complete cycle of a wave. For a transverse wave, the
wavelength is determined by measuring from crest to crest. A longitudinal wave
does not have crest; so how can its wavelength be determined? The wavelength
can always be determined by measuring the distance between any two
corresponding points on adjacent waves. In the case of a longitudinal wave, a
wavelength measurement is made by measuring the distance from a compression to
the next compression or from a rarefaction to the next rarefaction. On the
diagram above, the distance from point A to point C or from point B to point D
would be representative of the wavelength.
Check Your Understanding
Consider the diagram below in order to answer questions #1-2.

1. The wavelength of the wave in the diagram above is given
by letter ______.

Answer: A
The wavelength
is the distance from crest to crest (or from trough to trough) (or between any
two corresponding points on adjacent waves).
2. The amplitude of the wave in the diagram above is given by
letter _____.

Answer: D
The amplitude is
the distance from rest to crest or from rest to trough.
3. Indicate the interval that represents one full wavelength.
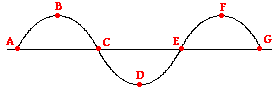
a. A to C
b. B to D
c. A to G
d. C to G

Answer: D
The wavelength
is the distance from crest to crest, trough to trough, or from a point on one
wave cycle to the corresponding point on the next adjacent wave cycle.