Pendulum Motion
A simple pendulum consists of a relatively
massive object hung by a string from a fixed support. It typically hangs
vertically in its equilibrium position. The massive object is affectionately
referred to as the pendulum bob. When the bob is displaced from equilibrium and then
released, it begins its back and forth vibration about its fixed equilibrium
position. The motion is regular and repeating, an example of periodic motion.
Pendulum motion was introduced earlier in
this lesson as we made an attempt to understand the nature of vibrating
objects. Pendulum motion was discussed again as we looked at the mathematical properties of objects
that are in periodic motion. Here we will investigate pendulum motion in even greater
detail as we focus upon how a variety of quantities change over the course of
time. Such quantities will include forces, position, velocity and energy - both
kinetic and potential energy.
Force
Analysis of a Pendulum
Earlier in this lesson we learned that an object that is vibrating is acted upon by a restoring
force. The restoring force causes the vibrating object to slow down as it moves
away from the equilibrium position and to speed up as it approaches the
equilibrium position. It is this restoring force that is responsible for the
vibration. So what forces act upon a pendulum bob? And what is the restoring
force for a pendulum? There are two dominant forces acting upon a pendulum bob at all times during
the course of its motion. There is the force of gravity that acts downward upon
the bob. It results from the Earth's mass attracting the mass of the bob. And
there is a tension force acting upward and towards the pivot point of the
pendulum. The tension force results from the string pulling upon the bob of the pendulum. In
our discussion, we will ignore the influence of
air resistance - a third force that always opposes the motion of the bob as it
swings to and fro. The air resistance force is relatively weak compared to the
two dominant forces.
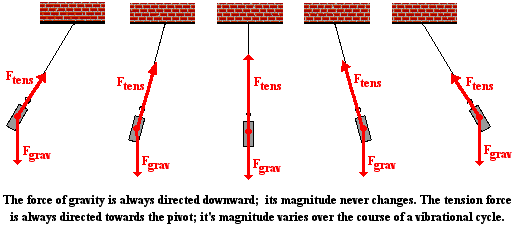
The gravity force is highly predictable; it is always in the
same direction (down) and always of the same magnitude - mass*9.8 N/kg. The
tension force is considerably less predictable. Both its direction and its
magnitude change as the bob swings to and fro. The direction of the tension
force is always towards the pivot point. So as the bob swings to the left of
its equilibrium position, the tension force is at an angle - directed upwards
and to the right. And as the bob swings to the right of its equilibrium
position, the tension is directed upwards and to the left. The diagram below
depicts the direction of these two forces at five different positions over the
course of the pendulum's path.
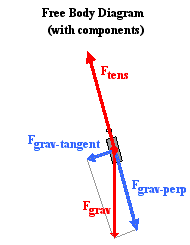In physical situations in which the forces acting on an object are not
in the same, opposite or perpendicular directions, it is customary to resolve
one or more of the forces into components. This was the practice used in the
analysis of sign hanging problems and inclined plane problems. Typically one or more of the
forces are resolved into perpendicular components that lie along coordinate
axes that are directed in the direction of the acceleration or perpendicular to
it. So in the case of a pendulum, it is the gravity force which gets resolved
since the tension force is already directed perpendicular to the motion. The
diagram at the right shows the pendulum bob at a position to the right of its
equilibrium position and midway to the point of maximum displacement. A
coordinate axis system is sketched on the diagram and the force of gravity is
resolved into two components that lie along these axes. One of the components
is directed tangent to the circular arc along which the pendulum bob moves;
this component is labeled Fgrav-tangent. The other component is directed
perpendicular to the arc; it is labeled Fgrav-perp. You will notice that the perpendicular
component of gravity is in the opposite direction of the tension force. You
might also notice that the tension force is slightly larger than this component
of gravity. The fact that the tension force (Ftens)
is greater than the perpendicular component of gravity (Fgrav-perp)
means there will be a net force which is perpendicular to the arc of the bob's
motion. This must be the case since we expect that objects that move
along circular paths will experience an inward or centripetal force. The tangential component of gravity (Fgrav-tangent)
is unbalanced by any other force. So there is a net force directed along the
other coordinate axes. It is this tangential component of gravity which acts as
the restoring force. As the pendulum bob moves to the right of the equilibrium
position, this force component is directed opposite its motion back towards the
equilibrium position.
The above analysis applies for a single location along the
pendulum's arc. At the other locations along the arc, the strength of the
tension force will vary. Yet the process of resolving gravity into two
components along axes that are perpendicular and tangent to the arc remains the
same. The diagram below shows the results of the force analysis for several
other positions.
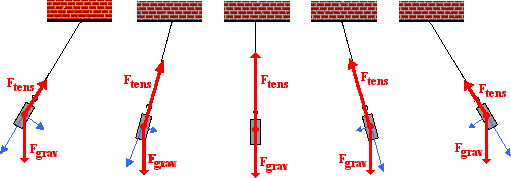
There are a couple comments to be made. First, observe the
diagram for when the bob is displaced to its maximum displacement to the right
of the equilibrium position. This is the position in which the pendulum bob
momentarily has a velocity of 0 m/s and is changing its direction. The tension
force (Ftens) and the perpendicular component of
gravity (Fgrav-perp) balance each other. At this
instant in time, there is no net force directed along the axis that is
perpendicular to the motion. Since the motion of the object is momentarily
paused, there is no need for a centripetal force.
Second, observe the diagram for when the bob is at the
equilibrium position (the string is completely vertical). When at this
position, there is no component of force along the tangent direction. When
moving through the equilibrium position, the restoring force is momentarily
absent. Having been restored to the equilibrium
position, there is no restoring force. The restoring force is only needed when
the pendulum bob has been displaced away from the equilibrium position. You
might also notice that the tension force (Ftens) is
greater than the perpendicular component of gravity (Fgrav-perp)
when the bob moves through this equilibrium position. Since the bob is in
motion along a circular arc, there must be a net centripetal force at this
position.
The Sinusoidal Nature of Pendulum Motion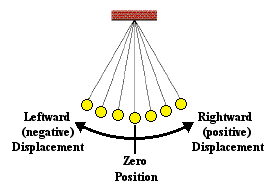
In the previous part of this lesson, we investigated the sinusoidal nature of the motion of a mass on a
spring. We will conduct a similar investigation here for the motion of a
pendulum bob. Let's suppose that we could measure the amount that the pendulum
bob is displaced to the left or to the right of its equilibrium or rest
position over the course of time. A displacement to the right of the
equilibrium position would be regarded as a positive displacement; and a
displacement to the left would be regarded as a negative displacement. Using this
reference frame, the equilibrium position would be regarded as the zero
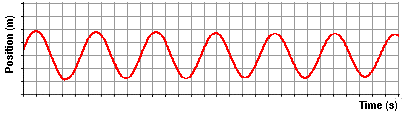
position. And suppose that we constructed a plot showing the variation in
position with respect to time. The resulting position vs. time plot is shown
below. Similar to what was observed for the mass on a spring, the position of
the pendulum bob (measured along the arc relative to its rest position) is a
function of the sine of the time.
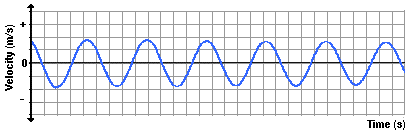
Now suppose that we use our motion detector to investigate
the how the velocity of the pendulum changes with respect to the time. As the
pendulum bob does the back and forth, the velocity is continuously changing. There will be times at which
the velocity is a negative value (for moving leftward) and other times at which
it will be a positive value (for moving rightward). And of course there will be
moments in time at which the velocity is 0 m/s. If the variations in velocity
over the course of time were plotted, the resulting graph would resemble the
one shown below.
Now let's try to understand the relationship between the
position of the bob along the arc of its motion and the velocity with which it
moves. Suppose we identify several locations along the arc and then relate
these positions to the velocity of the pendulum bob. The graphic below shows an
effort to make such a connection between position and velocity.
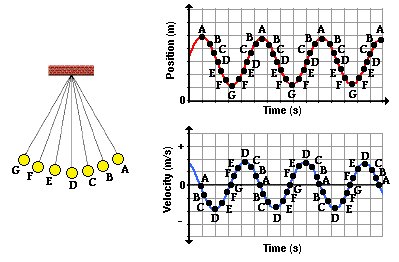
As is often said, a picture is worth a thousand words. Now
here come the words. The plot above is based upon the equilibrium position (D)
being designated as the zero position. A displacement to the left of the
equilibrium position is regarded as a negative position. A displacement to the
right is regarded as a positive position. An analysis of the plots shows that
the velocity is least when the displacement is greatest. And the velocity is
greatest when the displacement of the bob is least. The further the bob has
moved away from the equilibrium position, the slower it moves; and the closer
the bob is to the equilibrium position, the faster it moves. This can be
explained by the fact that as the bob moves away from the equilibrium position,
there is a restoring force that opposes its motion. This force slows the bob
down. So as the bob moves leftward from position D to E to F to G, the force
and acceleration is directed rightward and the velocity decreases as it moves
along the arc from D to G. At G - the maximum displacement to the left - the
pendulum bob has a velocity of 0 m/s. You might think of the bob as being momentarily
paused and ready to change its direction. Next the bob moves rightward along
the arc from G to F to E to D. As it does, the restoring force is directed to
the right in the same direction as the bob is moving. This force will
accelerate the bob, giving it a maximum speed at position D - the equilibrium
position. As the bob moves past position D, it is moving rightward alo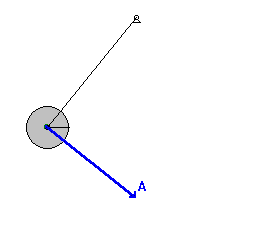
ng the arc towards C, then B and then A. As it does, there is a leftward
restoring force opposing its motion and causing it to slow down. So as the
displacement increases from D to A, the speed decreases due to the opposing
force. Once the bob reaches position A - the maximum displacement to the right
- it has attained a velocity of 0 m/s. Once again, the bob's velocity is least
when the displacement is greatest. The bob completes its cycle, moving leftward
from A to B to C to D. Along this arc from A to D, the restoring force is in
the direction of the motion, thus speeding the bob up. So it would be logical
to conclude that as the position decreases (along the arc from A to D), the
velocity increases. Once at position D, the bob will have a zero displacement
and a maximum velocity. The velocity is greatest when the displacement is
least. The animation at the right (used with the permission of Wikimedia Commons; special thanks to Hubert Christiaen)
provides a visual depiction of these principles. The acceleration vector that
is shown combines both the perpendicular and the tangential accelerations into
a single vector. You will notice that this vector is entirely tangent to the
arc when at maximum displacement; this is consistent with the force analysis
discussed above. And the vector is vertical (towards thecenter of
the arc) when at the equilibrium position. This also is consistent with the
force analysis discussed above.
Energy Analysis
In a previous chapter of The Physics
Classroom Tutorial, the energy possessed by a pendulum bob was discussed. We
will expand on that discussion here as we make an effort to associate the
motion characteristics described above with the concepts of kinetic energy, potential energy and total mechanical energy.
The kinetic energy possessed by an object is the energy it possesses due to its motion. It
is a quantity that depends upon both mass and speed. The equation that relates
kinetic energy (KE) to mass (m) and speed (v)
is
KE = ½mv2
The faster an object moves, the more kinetic energy that it
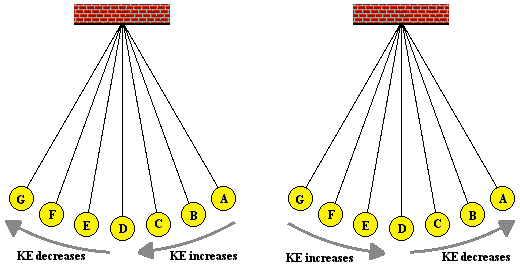
will possess. We can combine this concept with the discussion above about how
speed changes during the course of motion. This blending of concepts would lead
us to conclude that the kinetic energy of the pendulum bob increases as the bob
approaches the equilibrium position. And the kinetic energy decreases as the
bob moves further away from the equilibrium position.
The potential energy possessed by an
object is the stored energy of position. Two types of potential energy are
discussed in The Physics Classroom Tutorial - gravitational potential energy
and elastic potential energy. Elastic potential energy is only present when a
spring (or other elastic medium) is compressed or stretched. A simple pendulum
does not consist of a spring. The form of potential energy possessed by a
pendulum bob is gravitational potential energy. The amount of gravitational
potential energy is dependent upon the mass (m)
of the object and the height (h) of the
object. The equation for gravitational potential energy (PE)
is
PE = mgh
where g represents the gravitational field strength
(sometimes referred to as the acceleration caused by gravity) and has the value
of 9.8 N/kg.
The height of an object is expressed relative to some
arbitrarily assigned zero level. In other words,
the height must be measured as a vertical distance above some reference
position. For a pendulum bob, it is customary to call the lowest position the
reference position or the zero level. So when the bob is at the equilibrium
position (the lowest position), its height is zero and its potential energy is
0 J. As the pendulum bob does the back and forth, there are times during which the bob is moving away from the
equilibrium position. As it does, its height is increasing as it moves further
and further away. It reaches a maximum height as it reaches the position of
maximum displacement from the equilibrium position. As the bob moves towards
its equilibrium position, it decreases its height and decreases its potential
energy.
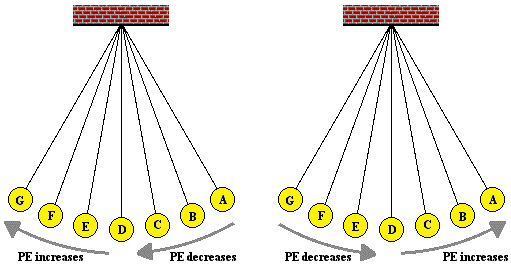
Now let's put these two concepts of kinetic energy and
potential energy together as we consider the motion of a pendulum bob moving
along the arc shown in the diagram at the right. We will use an energy bar chart to represent the
changes in the two forms of energy. The amount of each form of energy is
represented by a bar. The height of the bar is proportional to the amount of
that form of energy. In addition to the potential energy (PE)
bar and kinetic energy (KE) bar, there is a
third bar labeled TME. The TME bar represents the total amount of
mechanical energy possessed by the pendulum bob. The total mechanical
energy is simply the sum of the two forms of energy kinetic plus potential
energy. Take some time to inspect the bar charts shown below for positions A,
B, D, F and G. What do you notice?
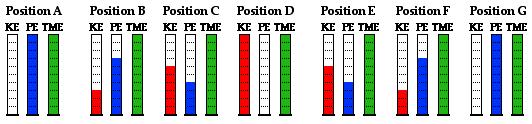
When you inspect the bar charts, it is evident that as the
bob moves from A to D, the kinetic energy is increasing and the potential
energy is decreasing. However, the total amount of these two forms of energy is
remaining constant. Whatever potential energy is lost in going from position A
to position D appears as kinetic energy. There is a transformation of potential
energy into kinetic energy as the bob moves from position A to position D. Yet
the total mechanical energy remains constant. We would say that mechanical
energy is conserved. As the bob moves past position D towards position G, the
opposite is observed. Kinetic energy decreases as the bob moves rightward and
(more importantly) upward toward position G. There is an increase in potential
energy to accompany this decrease in kinetic energy. Energy is being
transformed from kinetic form into potential form. Yet, as illustrated by the TME bar, the total amount of mechanical energy is
conserved. This very principle of energy conservation was explained in the Energy chapter of The Physics
Classroom Tutorial.
The Period
of a Pendulum
Our final discussion will pertain to the period of the
pendulum. As discussed previously in this lesson, the period is the time it takes for a vibrating object to complete its
cycle. In the case of pendulum, it is the time for the pendulum to start at one extreme, travel to the opposite extreme, and then return
to the original location. Here we will be interested in the question What variables affect the period of a pendulum? We will concern
ourselves with possible variables. The variables are the mass of the pendulum
bob, the length of the string on which it hangs, and the angular
displacement. The angular displacement or arc angle is the angle that
the string makes with the vertical when released from rest. These three
variables and their effect on the period are easily studied and are often the
focus of a physics lab in an introductory physics class. The data table below
provides representative data for such a study.
|
Trial |
Mass
(kg) |
Length
(m) |
Arc
Angle (°) |
Period
(s) |
|
1 |
0.02- |
0.40 |
15.0 |
1.25 |
|
2 |
0.050 |
0.40 |
15.0 |
1.29 |
|
3 |
0.100 |
0.40 |
15.0 |
1.28 |
|
4 |
0.200 |
0.40 |
15.0 |
1.24 |
|
5 |
0.500 |
0.40 |
15.0 |
1.26 |
|
6 |
0.200 |
0.60 |
15.0 |
1.56 |
|
7 |
0.200 |
0.80 |
15.0 |
1.79 |
|
8 |
0.200 |
1.00 |
15.0 |
2.01 |
|
9 |
0.200 |
1.20 |
15.0 |
2.19 |
|
10 |
0.200 |
0.40 |
10.0 |
1.27 |
|
11 |
0.200 |
0.40 |
20.0 |
1.29 |
|
12 |
0.200 |
0.40 |
25.0 |
1.25 |
|
13 |
0.200 |
0.40 |
30.0 |
1.26 |
In trials 1 through 5, the mass of the bob was
systematically altered while keeping the other quantities constant. By so
doing, the experimenters were able to investigate the possible effect of the
mass upon the period. As can be seen in these five trials, alterations in mass
have little effect upon the period of the pendulum.
In trials 4 and 6-9, the mass is held constant at 0.200 kg
and the arc angle is held constant at 15°. However, the length of the pendulum
is varied. By so doing, the experimenters were able to investigate the possible
effect of the length of the string upon the period. As can be seen in these
five trials, alterations in length definitely have an effect upon the period of
the pendulum. As the string is lengthened, the period of the pendulum is
increased. There is a direct relationship between the period and the length.
Finally, the experimenters investigated the possible effect
of the arc angle upon the period in trials 4 and 10-13. The mass is held
constant at 0.200 kg and the string length is held constant at 0.400 m. As can
be seen from these five trials, alterations in the arc angle have little to no
effect upon the period of the pendulum.
So the conclusion from such an experiment is that
the one variable that effects the period of the pendulum is the length of the
string. Increases in the length lead to increases in the period. But the
investigation doesn't have to stop there. The quantitative equation relating
these variables can be determined if the data is plotted and linear regression
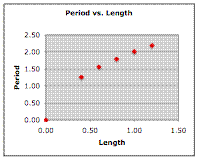
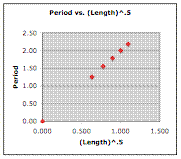
analysis is performed. The two plots below represent such an analysis. In each
plot, values of period (the dependent variable) are placed on the vertical
axis. In the plot on the left, the length of the pendulum is placed on the
horizontal axis. The shape of the curve indicates some sort of power
relationship between period and length. In the plot on the right, the square
root of the length of the pendulum (length to the ½ power) is plotted. The
results of the regression analysis are shown.
|
|
|
|
Slope: 1.7536 |
Slope: 2.0045 |
The analysis shows that there is a better fit of
the data and the regression line for the graph on the right. As such, the plot
on the right is the basis for the equation relating the period and the length.
For this data, the equation is
Period = 2.0045Length0.5 + 0.0077
Using T as the symbol for
period and L as the symbol for
length, the equation can be rewritten as
T = 2.0045L0.5 + 0.0077
The commonly reported equation based on theoretical
development is
T = 2Π(L/g)0.5
where g is a constant known as the gravitational field
strength or the acceleration of gravity (9.8 N/kg). The value of 2.0045 from
the experimental investigation agrees well with what would be expected from
this theoretically reported equation. Substituting the value of g into this equation, yields a proportionality
constant of 2Π/g0.5, which is 2.0071, very similar to the
2.0045 proportionality constant developed in the experiment.
Check Your Understanding
1. A pendulum bob is pulled back to position A and released from rest. The bob swings through its
usual circular arc and is caught at position C. Determine the position (A, B, C
or all the same) where the
a.
force of gravity is the greatest?
b.
restoring force is the greatest?
c.
speed is the greatest?
d.
potential energy is the greatest?
e.
kinetic energy is the greatest
f.
total mechanical energy is the greatest?
Answers:
a. The force of
gravity is everywhere the same since it is not dependent upon the pendulum's
position; it is always the product of mass and 9.8 N/kg.
b. The restoring force is greatest at A; the
further that the bob is from the rest position, the greater the restoring
force.
c. The speed is greatest at C. The restoring force accelerates the bob from
position A to position C. By the time the bob reaches C, it has accelerated to
its maximum speed.
d. The potential energy is the greatest at A. The potential energy is the
greatest at the highest position.
e. The kinetic energy is the greatest at position C; kinetic energy is greatest
at the lowest position. By the time the bob reaches C, all the original
potential energy has been transformed into kinetic energy.
f. The total mechanical energy is everywhere the same since energy is conserved
by a pendulum.
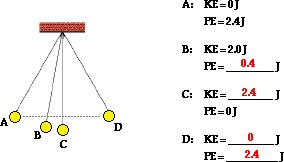
2. Use energy conservation to fill in the blanks in the
following diagram.
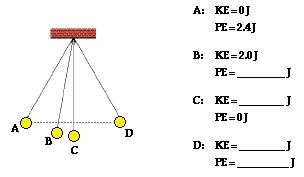
Answer: Energy is conserved. So the total amount of KE + PE
must be the same for each location.
3. A pair of trapeze performers at the circus is swinging
from ropes attached to a large elevated platform. Suppose that the performers
can be treated as a simple pendulum with a length of 16 m. Determine the period
for one complete back and forth cycle.
Answer: 8.0 s
Use the equation T = 2π(L/g).5
Insert 16 m in for L and 9.8 m/s2 in for g
T = 2πSQRT(16/9.8) = 8.028 s
(round to two significant digits)
4. Which would have the highest frequency of vibration?
Pendulum A: A 200-g mass attached to a 1.0-m length string
Pendulum B: A 400-g mass attached to a 0.5-m length string
Answer: Pendulum B
The mass of the
bob is not an important variable; only the length of the string will effect the period (and thus the frequency). Frequency
and period are inversely related. The pendulum with the smallest period will
have the highest frequency of vibration. A longer pendulum has a higher period;
a shorter pendulum will have a smaller period. Thus, the pendulum with the
shorter string will have a higher frequency of vibration.
5. Anna Litical wishes to
make a simple pendulum that serves as a timing device. She plans to make it
such that its period is 1.00 second. What length must the pendulum have?
Answer: 24.8 cm (0.248 m)
Use the equation T = 2π(L/g).5
Insert 1.00 s in for T and 9.8 m/s2 in for g. Give
attention to your algebra:
Square both sides of the equation to remove the radical.
The equation becomes L = T2g/(4π2).
The length comes
out to be 0.24824 m. Round to three significant digits.