Harmonics and Patterns

As mentioned earlier in Lesson 4, standing wave patterns are wave patterns produced in a medium when two waves of identical frequencies interfere in such a manner to produce points along the medium that always appear to be standing still. These points that have the appearance of standing still are referred to as nodes. Standing waves are often demonstrated in a Physics class using a snakey that is vibrated by the teacher at one end and held fixed at the other end by a student. The waves reflect off the fixed end and interfere with the waves introduced by the teacher to produce this regular and repeating pattern known as a standing wave pattern. A variety of actual wave patterns could be produced, with each pattern characterized by a distinctly different number of nodes. Such standing wave patterns can only be produced within the medium when it is vibrated at certain frequencies. There are several frequencies with which the snakey can be vibrated to produce the patterns. Each frequency is associated with a different standing wave pattern. These frequencies and their associated wave patterns are referred to as harmonics.

As discussed earlier in Lesson 4, the production of standing wave patterns demand that the introduction of crests and troughs into the medium be precisely timed. If the timing is not precise, then a regular and repeating wave pattern will not be discerned within the medium - a harmonic does not exist at such a frequency. 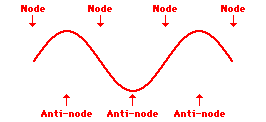With precise timing, reflected vibrations from the opposite end of the medium will interfere with vibrations introduced into the medium in such a manner that there are points that always appear to be standing still. These points of no displacement are referred to as nodes. Positioned in between every node is a point that undergoes maximum displacement from a positive position to a negative position. These points of maximum displacement are referred to as antinodes.


 

Examples of Standing Wave Patterns

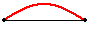
The simplest standing wave pattern that could be produced within a snakey is one that has points of no displacement (nodes) at the two ends of the snakey and one point of maximum displacement (antinode) in the middle. The animation below depicts the vibrational pattern observed when the medium is seen vibrating in this manner.

First Harmonic Standing Wave Pattern

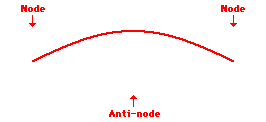
http://www.physicsclassroom.com/Class/waves/u10l4d1ani.webp

The above standing wave pattern is known as the first harmonic. It is the simplest wave pattern produced within the snakey and is obtained when the teacher introduced vibrations into the end of the medium at low frequencies.

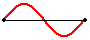
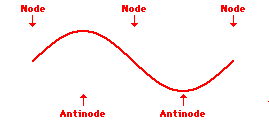
Other wave patterns can be observed within the snakey when it is vibrated at greater frequencies. For instance, if the teacher vibrates the end with twice the frequency as that associated with the first harmonic, then a second standing wave pattern can be achieved. This standing wave pattern is characterized by nodes on the two ends of the snakey and an additional node in the exact center of the snakey. As in all standing wave patterns, every node is separated by an antinode. This pattern with three nodes and two antinodes is referred to as the second harmonic and is depicted in the animation shown below.

Second Harmonic Standing Wave Pattern

http://www.physicsclassroom.com/Class/waves/u10l4d2ani.webp

 

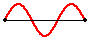
If the frequency at which the teacher vibrates the snakey is increased even more, then the third harmonic wave pattern can be produced within the snakey. The standing wave pattern for the third harmonic has an additional node and antinode between the ends of the snakey. The pattern is depicted in the animation shown below.

Third Harmonic Standing Wave Pattern

http://www.physicsclassroom.com/Class/waves/u10l4d3ani.webp


 

 

Numerical Patterns Associated with Standing Wave Diagrams

Observe that each consecutive harmonic is characterized by having one additional node and antinode compared to the previous one. The table below summarizes the features of the standing wave patterns for the first several harmonics.

Harmonic

# of Nodes

# of Antinodes

Pattern

1st

2

1

http://www.physicsclassroom.com/Class/waves/u10l4d4.webp

2nd

3

2

http://www.physicsclassroom.com/Class/waves/u10l4d5.webp

3rd

4

3

http://www.physicsclassroom.com/Class/waves/u10l4d6.webp

4th

5

4

http://www.physicsclassroom.com/Class/waves/u10l4d7.webp

5th

6

5

http://www.physicsclassroom.com/Class/waves/u10l4d8.webp

6th

7

6

http://www.physicsclassroom.com/Class/waves/u10l4d9.webp

nth

n + 1

n

--

 

As one studies harmonics and their standing wave patterns, it becomes evident that there is a predictability about them. Not surprisingly, this predictability expresses itself in a series of mathematical relationships that relate the wavelength of the wave pattern to the length of the medium. Additionally, the frequency of each harmonic is mathematically related to the frequency of the first harmonic. The next part of Lesson 4 will explore these mathematical relationships.



 

Flickr Physics Photo

A home-made wave machine was made using string, PVC pipe and connections, a battery, two motors and some wire. The wave machine does a great job producing the second and third harmonic standing wave patterns. The third harmonic is shown here. Observe the two nodes and the three antinodes positioned between the ends of the string.

Third Harmonic