Properties of Periodic Motion
A vibrating object is wiggling about a fixed position. Like
the mass on a spring in the animation at the right, a vibrating object is moving over the same path over the
course of time. Its motion repeats itself over and over again. If it were not
for damping, the vibrations would endure forever (or at least until
someone catches the mass and brings it to rest). The mass on the spring not
only repeats the same motion, it does so in a regular fashion. The time it
takes to complete one back and forth cycle is always the same amount of time.
If it takes the mass 3.2 seconds for the mass to complete the first back and
forth cycle, then it will take 3.2 seconds to complete the seventh back and
forth cycle. It's like clockwork. It's so predictable that you could set your
watch by it. In Physics, a motion that is regular and repeating is referred to
as a periodic motion. Most
objects that vibrate do so in a regular and repeated fashion; their vibrations
are periodic. (Special thanks to Oleg Alexandrov for the animation of the mass on a spring. It is a
public domain acquired from WikiMedia Commons. )
The
Sinusoidal Nature of a Vibration
Suppose that a motion detector was placed below a vibrating
mass on a spring in order to detect the changes in the mass's position over the
course of time. And suppose that the data from the motion detector could
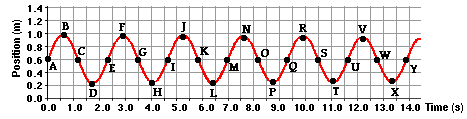
represent the motion of the mass by a position vs. time plot. The graphic below
depicts such a graph. For discussion sake, several points have been labeled on
the graph to assist in the follow-up discussion.
Before reading on, take a moment to reflect on the type of
information that is conveyed by the graph. And take a moment to reflect about
what quantities on the graph might be important in understanding the
mathematical description of a mass on a spring. If you've taken time to ponder
these questions, the following discussion will likely be more meaningful.
One obvious characteristic of the graph has to do with its
shape. Many students recognize the shape of this graph from experiences in
Mathematics class. The graph has the shape of a sine wave. If y = sine(x) is
plotted on a graphing calculator, a graph with this same shape would be
created. The vertical axis of the above graph represents the position of the
mass relative to the motion detector. A position of about 0.60 m cm above the
detector represents the resting position of the mass. So the mass is vibrating
back and forth about this fixed resting position over the course of time. There
is something sinusoidal about the vibration of a mass on a
spring. And the same can be said of a pendulum vibrating about a fixed position
or of a guitar string or of the air inside of a wind instrument. The position
of the mass is a function of the sine of the time.
A second obvious characteristic of the graph may be its
periodic nature. The motion repeats itself in a regular fashion. Time is being
plotted along the horizontal axis; so any measurement taken along this axis is
a measurement of the time for something to happen. A full cycle of
vibration might be thought of as the movement of the mass from its resting
position (A) to its maximum height (B), back down past its resting position (C)
to its minimum position (D), and then back to its resting position (E). Using
measurements from along the time axis, it is possible to determine the time for
one complete cycle. The mass is at position A at a time of 0.0 seconds and
completes its cycle when it is at position E at a time of 2.3 seconds. It takes
2.3 seconds to complete the first full cycle of vibration. Now if the motion of
this mass is periodic (i.e., regular and repeating), then it should take the
same time of 2.3 seconds to complete any full cycle of vibration. The same
time-axis measurements can be taken for the sixth full cycle of vibration. In
the sixth full cycle, the mass moves from a resting position (U) up to V, back
down past W to X and finally back up to its resting position (Y) in the time
interval from 11.6 seconds to 13.9 seconds. This represents a time of 2.3
seconds to complete the sixth full cycle of vibration. The two cycle times are
identical. Other cycle times are indicated in the table below. By inspection of
the table, one can safely conclude that the motion of the mass on a spring is
regular and repeating; it is clearly periodic. The small deviation from 2.3 s
in the third cyle can be accounted for by the lack of precision in the reading of
the graph.
|
Cycle |
Letters |
Times at Beginning and |
Cycle Time |
|
1st |
A to E |
0.0 sto 2.3
s |
2.3 |
|
2nd |
E tp I |
2.3 s to 4.6 s |
2.3 |
|
3rd |
I to M |
4.6 s to 7.0 s |
2.4 |
|
4th |
M to Q |
7.0 s to 9.3 s |
2.3 |
|
5th |
Q to U |
9.3 s to 11.6 s |
2.3 |
|
6th |
U to Y |
11.6 s to 13.9 s |
2.3 |
Students viewing the above graph will often describe the motion of the
mass as "slowing down." It might be too early to talk in detail about
what slowing down means. We will save the lengthy discussion of
the topic for the page later in this lesson devoted to the motion
of a mass on a spring. For now, let's simply say that over time, the
mass is undergoing changes in its speed in a sinusoidal fashion. That is, the
speed of the mass at any given moment in time is a function of the sine of the
time. As such, the mass will both speed up and slow down over the course of a
single cycle. So to say that the mass is "slowing down" is not
entirely accurate since during every cycle there are two short intervals during
which it speeds up. (More on this later.)
Students who describe the mass as slowing down (and most
observant students do describe it this way) are clearly observing something in
the graph features that draws out the "slowing down" comment. Before
we discuss the feature that triggers the "slowing down" comment, we
must re-iterate the conclusion from the previous paragraphs - the time to
complete one cycle of vibration is NOT changing. It took 2.3 seconds to
complete the first cycle and 2.3 seconds to complete the sixth cycle. Whatever
"slowing down" means, we must refute the notion that it means that
the cycles are taking longer as the motion continues. This notion is clearly
contrary to the data.
A third obvious characteristic of the graph is that damping
occurs with the mass-spring system. Some energy is being dissipated over the
course of time. The extent to which the mass moves above (B, F, J, N, R and V)
or below (D, H, L, P, T and X) the resting position (C, E, G, I, etc.) varies
over the course of time. In the first full cycle of vibration being shown, the
mass moves from its resting position (A) 0.60 m above the motion detector to a
high position (B) of 0.99 m cm above the motion detector. This is a total
upward displacement of 0.29 m. In the sixth full cycle of vibration that is
shown, the mass moves from its resting position (U) 0.60 m above the motion
detector to a high position (V) 0.94 m above the motion detector. This is a
total upward displacement of 0.24 m cm. The table below summarizes displacement
measurements for several other cycles displayed on the graph.
|
Cycle |
Letters |
Maximum
Upward |
Maximum
Downward |
|
1st |
A to E |
0.60 m to 0.99 m |
0.60 m to 0.21 m |
|
2nd |
E to I |
0.60 m to 0.98 m |
0.60 m to 0.22 m |
|
3rd |
I to M |
0.60 m to 0.97 m |
0.60 m to 0.23 m |
|
6th |
U to Y |
0.60 m to 0.94 m |
0.60 m to 0.26 m |
Over the course of time, the mass continues to vibrate -
moving away from and back towards the original resting position. However, the
amount of displacement of the mass at its maximum and minimum height is
decreasing from one cycle to the next. This illustrates that energy is being
lost from the mass-spring system. If given enough time, the vibration of the
mass will eventually cease as its energy is dissipated.
Perhaps, this observation of energy dissipation or energy loss is the
observation that triggers the "slowing down" comment discussed
earlier. In physics (or at least in the English language), "slowing
down" means to "get slower" or to "lose speed". Speed,
a physics term, refers to how fast or how slow an object is moving. To say that
the mass on the spring is "slowing down" over time is to say that its
speed is decreasing over time. But as mentioned (and as will be discussed in
great detail later), the mass speeds up during two intervals of
every cycle. As the restoring force pulls the mass back towards its resting
position (for instance, from B to C and from D to E), the mass speeds up. For
this reason, a physicist adopts a different language to communicate the idea
that the vibrations are "dying out". We use the phrase "energy
is being dissipated or lost" instead of saying the "mass is slowing
down." Language is important when it comes to learning physics. And
sometimes, faulty language (combined with surface-level thinking) can confuse a
student of physics who is sincerely trying to learn new ideas.
Period and Frequency
So far in this part of the lesson, we have looked at
measurements of time and position of a mass on a spring. The measurements were
based upon readings of a position-time graph. The data on the graph was
collected by a motion detector that was capturing a history of the
motion over the course of time. The key measurements that have been made are
measurements of:
· the time
for the mass to complete a cycle, and
· the maximum displacement of the mass above
(or below) the resting position.
These two measurable quantities have names. We call these
quantities period and amplitude.
An object that is in periodic motion - such as a mass on a spring, a
pendulum or a bobblehead doll - will undergo back and forth vibrations about
a fixed position in a regular and repeating fashion. The fact that the periodic
motion is regular and repeating means that it can be mathematically described
by a quantity known as the period. The period of the object's motion is defined
as the time for the object to complete one full cycle. Being a time, the period
is measured in units such as seconds, milliseconds, days or even years. The
standard metric unit for period is the second.
An object in periodic motion can have a long period or a short period.
For instance, a pendulum bob tied to a 1-meter length string has a period of
about 2.0 seconds. For comparison sake, consider the vibrations of a piano
string that plays the middle C note (the C
note of the fourth octave). Its period is approximately 0.0038 seconds (3.8
milliseconds). When comparing these two vibrating objects - the 1.0-meter
length pendulum and the piano string which plays the middle C
note - we would describe the piano string as vibrating relatively frequently
and we would describe the pendulum as vibrating relatively infrequently.
Observe that the description of the two objects uses the terms frequentlyand infrequently. The terms fast and slow are not
used since physics types reserve the words fast and slowtorefer to an object's speed. Here in this description we are referring to
the frequency, not the speed. An object can be in periodic motion and have a
low frequency and a high speed. As an example, consider the periodic motion of
the moon in orbit about the earth. The moon moves very fast; its orbit is
highly infrequent. It moves through space with a speed of about 1000 m/s -
that's fast. Yet it makes a complete cycle about the earth once every 27.3 days
(a period of about 2.4x105 seconds) - that's infrequent.
Objects like the piano string that have a relatively short
period (i.e., a low value for period) are said to have a high frequency.
Frequency is another quantity that can be used to quantitatively describe the
motion of an object is periodic motion. The frequency is defined as the number of complete cycles
occurring per period of time. Since the standard metric unit of time is the
second, frequency has units of cycles/second. The unit cycles/second is
equivalent to the unit Hertz (abbreviated Hz). The unit Hertz is used in honor of Heinrich
Rudolf Hertz, a 19th century physicist who expanded our understanding of the
electromagnetic theory of light waves.
The concept and quantity frequency is best
understood if you attach it to the everyday English meaning of the word.
Frequency is a word we often use to describe how often something occurs. You
might say that you frequently check your email or you frequently talk to a
friend or you frequently wash your hands when working with chemicals. Used in
this context, you mean that you do these activities often. To say that you
frequently check your email means that you do it several times a day - you do
it often. In physics, frequency is used with the same meaning - it indicates
how often a repeated event occurs. High frequency events that are periodic
occur often, with little time in between each occurrence - like the back and
forth vibrations of the tines of a tuning fork. The vibrations are so frequent
that they can't be seen with the naked eye. A 256-Hz tuning fork has tines that
make 256 complete back and forth vibrations each second. At this frequency, it
only takes the tines about 0.00391 seconds to complete one cycle. A 512-Hz
tuning fork has an even higher frequency. Its vibrations occur more frequently;
the time for a full cycle to be completed is 0.00195 seconds. In comparing
these two tuning forks, it is obvious that the tuning fork with the highest
frequency has the lowest period. The two quantities frequency and period are
inversely related to each other. In fact, they are mathematical reciprocals of
each other. The frequency is the reciprocal of the period and the period is the
reciprocal of the frequency.
This reciprocal relationship is easy to
understand. After all, the two quantities are conceptual reciprocals(a phrase I made up). Consider their definitions
as restated below:
· period =
the time for one full cycle to complete itself; i.e., seconds/cycle
· frequency
= the number of cycles that are completed per time; i.e., cycles/second
Even the definitions have a reciprocal
ring to them. To understand the distinction between period and frequency,
consider the following statement:
According
to Wikipedia (and as of this writing), Tim Ahlstrom of Oconomowoc, WI holds the
record for hand clapping. He is reported to have clapped his hands 793 times in
60.0 seconds.
What is the frequency and what is the period of
Mr. Ahlstrom's hand clapping during this 60.0-second period?
In
this problem, the event that is repeating itself is the clapping of hands; one
hand clap is equivalent to a cycle.
Frequency
= cycles per second = 793 cycles/60.0 seconds = 13.2 cycles/s = 13.2 Hz
Period
= seconds per cycle = 60.0 s/793 cycles = 0.0757 seconds
Amplitude of Vibration
The final measurable quantity that describes a vibrating
object is the amplitude. The amplitude is defined as the maximum displacement
of an object from its resting position. The resting position is that position assumed by the object when not
vibrating. Once vibrating, the object oscillates about this fixed position. If
the object is a mass on a spring (such as the discussion earlier on this page),
then it might be displaced a maximum distance of 35 cm below the resting
position and 35 cm above the resting position. In this case, the amplitude of
motion is 35 cm.
Over the course of time, the amplitude of a vibrating object
tends to become less and less. The amplitude of motion is a reflection of the
quantity of energy possessed by the vibrating object. An object vibrating with
a relatively large amplitude has a relatively large amount of energy. Over
time, some of this energy is lost due to damping. As the energy is lost, the amplitude
decreases. If given enough time, the amplitude decreases to 0 as the object
finally stops vibrating. At this point in time, it has lost all its energy.
Check Your Understanding
1. A pendulum is observed to complete 23 full cycles in 58
seconds. Determine the period and the frequency of the pendulum.
The
frequency can be thought of as the number of cycles per second. Calculating
frequency involves dividing the stated number of cycles by the corresponding
amount of time required to complete these cycles. In contrast, the period is
the time to complete a cycle. Period is calculated by dividing the given time
by the number of cycles completed in this amount of time.
frequency = 23 cycles/58 seconds = 0.39655 Hz = ~0.40 Hz
period = 58 seconds/23 cycles = 2.5217 sec = ~2.5 s
2. A mass is tied to a spring and begins vibrating
periodically. The distance between its highest and its lowest position is 38
cm. What is the amplitude of the vibrations?
Answer: 19 cm
The distance
that is described is the distance from the high position to the low position.
The amplitude is from the middle position to either the high or the low
position.