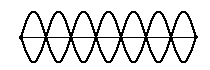
Nodes and Anti-nodes
As
mentioned earlier in
Lesson 4, a standing wave pattern is an interference phenomenon. It is
formed as the result of the perfectly timed interference of two waves passing
through the same medium. A standing wave pattern is not actually a wave; rather
it is the pattern resulting from the presence of two waves of the same
frequency with different directions of travel within the same medium.
 What are Nodes and
Antinodes?
What are Nodes and
Antinodes?
One
characteristic of every standing wave pattern is that there are points along
the medium that appear to be standing still. These points, sometimes described
as points of no displacement, are referred to as nodes. There are other points along the
medium that undergo vibrations between a large positive and large negative
displacement. These are the points that undergo the maximum displacement during
each vibrational cycle of the standing wave. In a sense, these points are the
opposite of nodes, and so they are called antinodes. A standing wave pattern always
consists of an alternating pattern of nodes and antinodes. The animation shown
below depicts a rope vibrating with a standing wave pattern. The nodes and
antinodes are labeled on the diagram. When
a standing wave pattern is established in a medium, the nodes and the antinodes
are always located at the same position along the medium; they are standing still. It is
this characteristic that has earned the pattern the name standing wave.
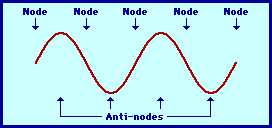
Flickr Physics Photo
A standing wave is established upon a vibrating
string using a harmonic oscillator and a frequency generator. A strobe is used
to illuminate the string several times during each cycle. The finger is
pointing at a nodal position.
Standing Wave
Diagrams
The
positioning of the nodes and antinodes in a standing wave pattern can be
explained by focusing on the interference of the two waves. The nodes are
produced at locations where destructive interference occurs. For instance,
nodes form at locations where a crest of one wave meets a trough of a second
wave; or a half-crest of one wave meets a half-trough of a second wave; or a quarter-crest of one wave meets a quarter-trough of a second wave; etc. Antinodes,
on the other hand, are produced at locations where constructive interference
occurs. For instance, if a crest of one wave meets a crest of a second wave, a
point of large positive displacement results. Similarly, if a trough of one
wave meets a trough of a second wave, a point of large negative displacement
results. Antinodes are always vibrating back and forth between these points of
large positive and large negative displacement; this is because during a
complete cycle of vibration, a crest will meet a crest; and then one-half cycle
later, a trough will meet a trough. Because antinodes are vibrating back and
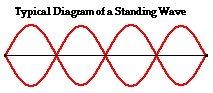
forth between a large positive and large negative displacement, a diagram of a
standing wave is sometimes depicted by drawing the shape of the medium at an
instant in time and at an instant one-half vibrational cycle later. This is
done in the diagram below.
Nodes
and antinodes should not be confused with crests and troughs. When the motion
of a traveling
wave is
discussed, it is customary to refer to a point of large maximum displacement as
a crest and a point of large negative displacement as
a trough. These
represent points of the
disturbance that
travel from one location to another through the medium. An antinode on the
other hand is a point on the
medium that is
staying in the same location. Furthermore, an antinode vibrates back and forth
between a large upward and a large downward displacement. And finally, nodes
and antinodes are not actually part of a wave. Recall that a standing wave is
not actually a wave but rather a pattern that results from the interference of
two or more waves. Since a standing wave is not technically a wave, an antinode
is not technically a point on a wave. The nodes and antinodes are merely unique
points on the medium that make up the wave pattern.
Watch It!
A physics instructor demonstrates and explains the formation of
a longitudinal standing wave in a spring.
Check Your Understanding
1.
Suppose that there was a ride at an amusement park that was titled The Standing Wave. Which
location - node or antinode - on the ride would give the greatest thrill?

Answer: The antinode
The antinode is
continually vibrating from a high to a low displacement - now that would be a
ride.
2.
A standing wave is formed when ____.
a. a wave refracts due to changes in the properties of the medium.
b. a wave reflects off a canyon wall and is heard shortly after
it is formed.
c. red, orange, and yellow wavelengths bend around suspended
atmospheric particles.
d. two identical waves moving different directions along
the same medium interfere.

Answer: D
If still
uncertain, then review the previous page of Lesson 4.
|
3. The number of nodes in the standing wave shown in the
diagram at the right is ____.
|
|

Answer: C (8 nodes)
There are eight
positions along the medium which have no displacement. Be sure to avoid the
common mistake of not counting the end positions.
4.
The number of antinodes in the standing wave shown in the diagram above right
is ____.
|
a. 6 |
b. 7 |
c. 8 |
d. 14 |

Answer: B (7 antinodes)
There are seven positions along the medium which have vibrate
between a large positive and a large negative displacement.
Be sure to avoid
the common mistake of counting the antinodal positions
twice. An antinode is simply a point along a medium which undergoes maximum
displacement above and below the rest position. Do not count these positions
twice.
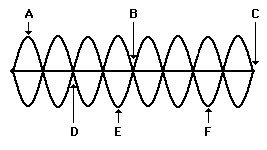
Consider
the standing wave pattern at the right in answering these next two questions.
|
5. The
number of nodes in the entire pattern is ___.
Answer: C (9 nodes) There are nine positions
along the medium which have no displacement. (Be sure to avoid the common
mistake of not counting the end positions.) |
|
6. Of all the labeled points, destructive
interference occurs at point(s) ____.
|
a. B, C,
and D |
b. A, E,
and F |
c. A only |
|
d. C only |
e. all
points |
|

Answer: A
Destructive
interference has occurred at points B, C and D to produce the nodes which are
seen at these points.