Interference of Waves
What happens when two waves meet while they travel through
the same medium? What effect will the meeting of the waves have upon the
appearance of the medium? Will the two waves bounce off each other upon meeting
(much like two billiard balls would) or will the two waves pass through each
other? These questions involving the meeting of two or more waves along the
same medium pertain to the topic of wave interference.
What
is Interference?
Wave interference is the
phenomenon that occurs when two waves meet while traveling along the same
medium. The interference of waves causes the medium to take on a shape that
results from the net effect of the two individual waves upon the particles of
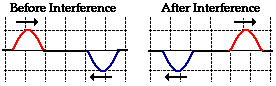
the medium. To begin our exploration of wave interference, consider two pulses
of the same amplitude traveling in different directions along the same medium.
Let's suppose that each displaced upward 1 unit at its crest and has the shape
of a sine wave. As the sine pulses move towards each other, there will
eventually be a moment in time when they are completely overlapped. At that
moment, the resulting shape of the medium would be an upward displaced sine
pulse with an amplitude of 2 units. The diagrams below depict the before and
during interference snapshots of the medium for two such pulses. The individual
sine pulses are drawn in red and blue and the resulting displacement of the
medium is drawn in green.
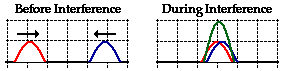
Constructive Interference
This type of interference is sometimes called constructive
interference. Constructive interference is a type of interference that occurs at any
location along the medium where the two interfering waves have a displacement
in the same direction. In this case, both waves have an upward displacement;
consequently, the medium has an upward displacement that is greater than the
displacement of the two interfering pulses. Constructive interference is
observed at any location where the two interfering waves are displaced upward.
But it is also observed when both interfering waves are displaced downward.
This is shown in the diagram below for two downward displaced pulses.
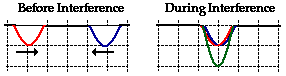
In this case, a sine pulse with a maximum displacement of -1
unit (negative means a downward displacement) interferes with a sine pulse with
a maximum displacement of -1 unit. These two pulses are drawn in red and blue.
The resulting shape of the medium is a sine pulse with a maximum displacement
of -2 units.
Destructive Interference
Destructive interference is a type
of interference that occurs at any location along the medium where the two
interfering waves have a displacement in the opposite direction. For instance,
when a sine pulse with a maximum displacement of +1 unit meets a sine pulse
with a maximum displacement of -1 unit, destructive interference occurs. This
is depicted in the diagram below.
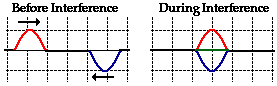
In the diagram above, the interfering pulses have the same
maximum displacement but in opposite directions. The result is that the two
pulses completely destroy each other when they are completely overlapped. At
the instant of complete overlap, there is no resulting displacement of the
particles of the medium. This "destruction" is not a permanent condition.
In fact, to say that the two waves destroy each other can be partially
misleading. When it is said that the two pulses destroy each other, what is
meant is that when overlapped, the effect of one of the pulses on the
displacement of a given particle of the medium is destroyed or canceled by the effect of the other pulse. Recall
from Lesson 1 that waves transport energy through a medium by means of each individual
particle pulling upon its nearest neighbor. When two pulses with opposite displacements
(i.e., one pulse displaced up and the other down) meet at a given location, the
upward pull of one pulse is balanced (canceled or destroyed) by the downward pull of the
other pulse. Once the two pulses pass through each other, there is still an
upward displaced pulse and a downward displaced pulse heading in the same
direction that they were heading before the interference. Destructive
interference leads to only a momentary condition in which the medium's
displacement is less than the displacement of the largest-amplitude wave.
The two interfering waves do not need to have equal
amplitudes in opposite directions for destructive interference to occur. For
example, a pulse with a maximum displacement of +1 unit could meet a pulse with
a maximum displacement of -2 units. The resulting displacement of the medium
during complete overlap is -1 unit.
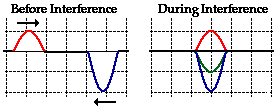
This is still destructive interference since the two
interfering pulses have opposite displacements. In this case, the destructive
nature of the interference does not lead to complete cancellation.
Interestingly, the meeting of two waves along a medium does
not alter the individual waves or even deviate them from their path. This only
becomes an astounding behavior when it is compared to what happens when two billiard balls meet
or two football players meet. Billiard balls might crash and bounce off each
other and football players might crash and come to a stop. Yet two waves will
meet, produce a net resulting shape of the medium, and then continue on doing
what they were doing before the interference.
The Principle of Superposition
The task of determining the shape of the resultant demands
that the principle of superposition is applied. The principle of
superposition is sometimes stated as follows:
|
When two
waves interfere, the resulting displacement of the medium at any location is
the algebraic sum of the displacements of the individual waves at that same
location. |
In the cases above, the summing the individual displacements
for locations of complete overlap was made out to be an easy task - as easy as
simple arithmetic:
|
Displacement of Pulse 1 |
Displacement of Pulse 2 |
= |
Resulting Displacement |
|
+1 |
+1 |
= |
+2 |
|
-1 |
-1 |
= |
-2 |
|
+1 |
-1 |
= |
0 |
|
+1 |
-2 |
= |
-1 |
In actuality, the task of determining the complete shape of
the entire medium during interference demands that the principle of
superposition be applied for every point (or nearly every point) along the
medium. As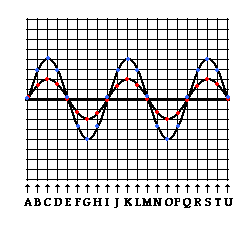 
an example of the complexity of this task, consider the two interfering
waves at the right. A snapshot of the shape of each individual wave at a
particular instant in time is shown. To determine the precise shape of the
medium at this given instant in time, the principle of superposition must be applied
to several locations along the medium. A short cut involves measuring the
displacement from equilibrium at a few strategic locations. Thus, approximately
20 locations have been picked and labeled as A, B, C, D, etc. The actual
displacement of each individual wave can be counted by measuring from the
equilibrium position up to the particular wave. At position A, there is no
displacement for either individual wave; thus, the resulting displacement of
the medium at position will be 0 units. At position B, the smaller wave has a
displacement of approximately 1.4 units (indicated by the red dot); the larger
wave has a displacement of approximately 2 units (indicated by the blue dot).
Thus, the resulting displacement of the medium will be approximately 3.4 units.
At position C, the smaller wave has a displacement of approximately 2 units;
the larger wave has a displacement of approximately 4 units; thus, the
resulting displacement of the medium will be approximately 6 units. At position
D, the smaller wave has a displacement of approximately 1.4 units; the larger
wave has a displacement of approximately 2 units; thus, the resulting
displacement of the medium will be approximately 3.4 units. This process can be
repeated for every position. When finished, a dot (done in green below) can be
marked on the graph to note the displacement of the medium
at each given location. The actual shape of the medium can then be sketched by
estimating the position between the various marked points and sketching the
wave. This is shown as the green line in the diagram below.
Check Your Understanding
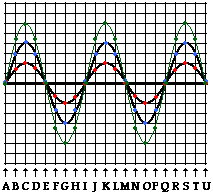
1. Several positions along the medium are labeled with
a letter. Categorize each labeled position along the medium as being a
position where either constructive or destructive interference occurs.
Constructive
Interference: G, J, M and N
Destructive
Interference: H, I, K, L,
and O
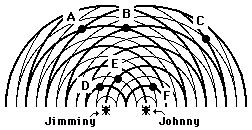2. Twin water bugs Jimminy and Johnny are both creating a series of
circular waves by jiggling their legs in the water. The waves undergo
interference and create the pattern represented in the diagram at the right.
The thick lines in the diagram represent wave crests and the thin lines
represent wave troughs. Several of positions in the water are labeled with
a letter. Categorize each labeled position as being a position where either
constructive or destructive interference occurs.
Constructive Interference: A and B
Destructive
Interference: C, D, E, and F