The Wave Equation
As
was discussed in Lesson 1, a
wave is produced when a vibrating source periodically disturbs the first
particle of a medium. This creates a wave pattern that begins to travel along
the medium from particle to particle. The frequency at which each individual particle vibrates is
equal to the frequency at which the source vibrates. Similarly, the period of vibration
of each individual particle in the medium is equal to the period of vibration
of the source. In one period, the source is able to displace the first particle
upwards from rest, back to rest, downwards from rest, and finally back to rest.
This complete back-and-forth movement constitutes one complete wave cycle.
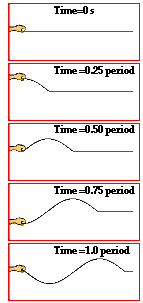The diagrams
at the right show several "snapshots" of the production of a wave
within a rope. The motion of the disturbance along the medium after every
one-fourth of a period is depicted. Observe that in the time it takes from the
first to the last snapshot, the hand has made one complete back-and-forth
motion. A period has elapsed. Observe that during this same
amount of time, the leading edge of the disturbance has moved a distance equal
to one complete wavelength. So in a time of one period, the wave has moved a
distance of one wavelength. Combining this information with the equation for
speed (speed = distance/time), it can be said that the speed of a wave is also
the wavelength/period.
Since
the period is the reciprocal of the frequency, the expression 1/f can be
substituted into the above equation for period. Rearranging the equation yields
a new equation of the form:
Speed = Wavelength • Frequency
The
above equation is known as the wave equation. It states the mathematical
relationship between the speed (v) of a wave and its wavelength (λ)
and frequency (f). Using the symbols v, λ, and f, the equation can be rewritten as
v = f • λ
As
a test of your understanding of the wave equation and its mathematical use
in analyzing wave motion, consider the
following three-part question:
Stan
and Anna are conducting a slinky experiment. They are studying the possible
effect of several variables upon the speed of a wave in a slinky. Their data
table is shown below. Fill in the blanks in the table, analyze the
data, and answer the following questions.
|
Medium |
Wavelength |
Frequency |
Speed |
|
Zinc, 1-in. dia. coils |
1.75 m |
2.0 Hz |
______ |
|
Zinc, 1-in. dia. coils |
0.90 m |
3.9 Hz |
______ |
|
Copper, 1-in. dia. coils |
1.19 m |
2.1 Hz |
______ |
|
Copper, 1-in. dia. coils |
0.60 m |
4.2 Hz |
______ |
|
Zinc, 3-in. dia. coils |
0.95 m |
2.2 Hz |
______ |
|
Zinc, 3-in. dia. coils |
1.82 m |
1.2 Hz |
______ |
1.
As the wavelength of a wave in a uniform medium increases, its speed will
_____.
|
a. decrease |
b. increase |
c. remain the same |
2.
As the wavelength of a wave in a uniform medium increases, its frequency will
_____.
|
a. decrease |
b. increase |
c. remain the same |
3.
The speed of a wave depends upon (i.e., is causally affected by) ...
a. the properties of the medium through which the wave travels
b. the wavelength of the wave.
c. the frequency of the wave.
d. both the wavelength and the frequency of the wave.
The
above example illustrates how to use the wave equation to solve mathematical
problems. It also illustrates the principle that wave speed is dependent upon medium properties and independent of wave properties. Even though
the wave speed is calculated by multiplying wavelength by frequency, an
alteration in wavelength does not affect wave speed. Rather, an alteration in
wavelength affects the frequency in an inverse manner. A doubling of the
wavelength results in a halving of the frequency; yet the wave speed is not
changed.
Check Your Understanding
1.
Two waves on identical strings have frequencies in a ratio of 2 to 1. If their
wave speeds are the same, then how do their wavelengths compare?
|
a. 2:1 |
b. 1:2 |
c. 4:1 |
d. 1:4 |
Answer: B
Frequency and
wavelength are inversely proportional to each other. The wave with the greatest
frequency has the shortest wavelength. Twice the frequency means one-half the
wavelength. For this reason, the wavelength ratio is the inverse of the
frequency ratio.
2.
Mac and Tosh stand 8 meters apart and demonstrate the motion of a transverse
wave on a snakey. The wave e can be described as
having a vertical distance of 32 cm from a trough to a crest, a frequency of
2.4 Hz, and a horizontal distance of 48 cm from a crest to the nearest trough.
Determine the amplitude, period, and wavelength and speed of such a wave.
Amplitude = 16 cm
(Amplitude is the
distance from the rest position to the crest position which is half the
vertical distance from a trough to a crest.)
Wavelength = 96 cm
(Wavelength is the
distance from crest to crest, which is twice the horizontal distance from crest
to nearest trough.)
Period = 0.42 s
(The period is the
reciprocal of the frequency. T = 1 / f)
Speed = 230 cm/s
(The speed of a
wave is calculated as the product of the frequency times the wavelength.)
3.
Dawn and Aram have stretched a slinky between them and begin experimenting with
waves. As the frequency of the waves is doubled,
a. the wavelength is halved and the speed remains constant
b. the wavelength remains constant and the speed is doubled
c. both the wavelength and the speed are halved.
d. both the wavelength and the speed remain constant.
Answer: A
Doubling the
frequency will not alter the wave speed. Rather, it will halve the wavelength.
Wavelength and frequency are inversely related.
4.
A ruby-throated hummingbird beats its wings at a rate of about 70 wing beats
per second.
a.
What is the frequency in Hertz of the sound wave?
b.
Assuming the sound wave moves with a velocity of 350 m/s, what is the
wavelength of the wave?
Answer: f = 70 Hz and λ = 5.0 m
The frequency is
given and the wavelength is the v/f ratio.
5.
Ocean waves are observed to travel along the water surface during a developing
storm. A Coast Guard weather station observes that there is a vertical distance
from high point to low point of 4.6 meters and a horizontal distance of 8.6
meters between adjacent crests. The waves splash into the station once every
6.2 seconds. Determine the frequency and the speed of these waves.
The wavelength is 8.6 meters and the period is 6.2 seconds.
The frequency can be determined from the period. If T = 6.2 s, then
f =1 /T = 1 / (6.2
s)
f = 0.161 Hz
Now find speed using the v = f • λ equation.
v = f • λ =
(0.161 Hz) • (8.6 m)
v = 1.4 m/s
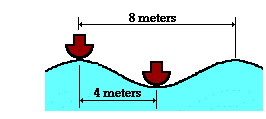
6.
Two boats are anchored 4 meters apart. They bob up and down, returning to the
same up position every 3 seconds. When one is up the other is down. There are
never any wave crests between the boats. Calculate the speed of the waves.
The diagram is helpful. The wavelength must be 8 meters (see
diagram).
The period is 3 seconds so the frequency is 1 / T or 0.333 Hz.
Now use speed = f
• wavelength Substituting and solving for v, you will get 2.67 m/s.