Vibrational Motion

Things wiggle. They do the back and forth. They vibrate; they shake; they oscillate. These phrases describe the motion of a variety of objects. They even describe the motion of matter at the atomic level. Even atoms wiggle - they do the back and forth. Wiggles, vibrations, and oscillations are an inseparable part of nature. In this chapter of The Physics Classroom Tutorial, we will make an effort to understand vibrational motion and its relationship to waves. An understanding of vibrations and waves is essential to understanding our physical world. Much of what we see and hear is only possible because of vibrations and waves. We see the world around us because of light waves. And we hear the world around us because of sound waves. If we can understand waves, then we will be able to understand the world of sight and sound.

Bobblehead Dolls - An Example of a Vibrating Object

To begin our ponderings of vibrations and waves, consider one of those crazy bobblehead dolls that you've likely seen at baseball stadiums or novelty shops. A bobblehead doll consists of an oversized replica of a person's head attached by a spring to a body and a stand. A light tap to the oversized head causes it to bobble. The head wiggles; it vibrates; it oscillates. When pushed or somehow disturbed, the head does the back and forth. The back and forth doesn't happen forever. Over time, the vibrations tend to die off and the bobblehead stops bobbing and finally assumes its usual resting position.

The bobblehead doll is a good illustration of many of the principles of vibrational motion. Think about how you would describe the back and forth motion of the oversized head of a bobblehead doll. What words would you use to describe such a motion? How does the motion of the bobblehead change over time? How does the motion of one bobblehead differ from the motion of another bobblehead? What quantities could you measure to describe the motion and so distinguish one motion from another motion? How would you explain the cause of such a motion? Why does the back and forth motion of the bobblehead finally stop? These are all questions worth pondering and answering if we are to understand vibrational motion. These are the questions we will attempt to answer in Section 1 of this chapter.

What Causes Objects to Vibrate?

Like any object that undergoes vibrational motion, the bobblehead has a resting position. The resting position is the position assumed by the bobblehead when it is not vibrating. The resting position is sometimes referred to as the equilibrium position. When an object is positioned at its equilibrium position, it is in a state of equilibrium. As discussed in the Newton's Law Chapter of the Tutorial, an object which is in a state of equilibrium is experiencing a balance of forces. All the individual forces - gravity, spring, etc. - are balanced or add up to an overall net force of 0 Newtons. When a bobblehead is at the equilibrium position, the forces on the bobblehead are balanced. The bobblehead will remain in this position until somehow disturbed from its equilibrium.

If a force is applied to the bobblehead, the equilibrium will be disturbed and the bobblehead will begin vibrating. We could use the phrase forced vibration to describe the force which sets the otherwise resting bobblehead into motion. In this case, the force is a short-lived, momentary force that begins the motion. The bobblehead does its back and forth, repeating the motion over and over. Each repetition of its back and forth motion is a little less vigorous than its previous repetition. If the head sways 3 cm to the right of its equilibrium position during the first repetition, it may only sway 2.5 cm to the right of its equilibrium position during the second repetition. And it may only sway 2.0 cm to the right of its equilibrium position during the third repetition. And so on. The extent of its displacement from the equilibrium position becomes less and less over time. Because the forced vibration that initiated the motion is a single instance of a short-lived, momentary force, the vibrations ultimately cease. The bobblehead is said to experience damping. Damping is the tendency of a vibrating object to lose or to dissipate its energy over time. The mechanical energy of the bobbing head is lost to other objects. Without a sustained forced vibration, the back and forth motion of the bobblehead eventually ceases as energy is dissipated to other objects. A sustained input of energy would be required to keep the back and forth motion going. After all, if the vibrating object naturally loses energy, then it must continuously be put back into the system through a forced vibration in order to sustain the vibration.

The Restoring Force

A vibrating bobblehead often does the back and forth a number of times. The vibrations repeat themselves over and over. As such, the bobblehead will move back to (and past) the equilibrium position every time it returns from its maximum displacement to the right or the left (or above or below). This begs a question - and perhaps one that you have been thinking of yourself as you've pondered the topic of vibration. If the forces acting upon the bobblehead are balanced when at the equilibrium position, then why does the bobblehead sway past this position? Why doesn't the bobblehead stop the first time it returns to the equilibrium position? The answer to this question can be found in Newton's first law of motion. Like any moving object, the motion of a vibrating object can be understood in light of Newton's laws. According to Newton's law of inertia, an object which is moving will continue its motion if the forces are balanced. Put another way, forces, when balanced, do not stop moving objects. So every instant in time that the bobblehead is at the equilibrium position, the momentary balance of forces will not stop the motion. The bobblehead keeps moving. It moves past the equilibrium position towards the opposite side of its swing. As the bobblehead is displaced past its equilibrium position, then a force capable of slowing it down and stopping it exists. This force that slows the bobblehead down as it moves away from its equilibrium position is known as a restoring force. The restoring force acts upon the vibrating object to move it back to its original equilibrium position.

Vibrational motion is often contrasted with translational motion. In translational motion, an object is permanently displaced. The initial force that is imparted to the object displaces it from its resting position and sets it into motion. Yet because there is no restoring force, the object continues the motion in its original direction. When an object vibrates, it doesn't move permanently out of position. The restoring force acts to slow it down, change its direction and force it back to its original equilibrium position. An object in translational motion is permanently displaced from its original position. But an object in vibrational motion wiggles about a fixed position - its original equilibrium position. Because of the restoring force, vibrating objects do the back and forth. We will explore the restoring force in more detail later in this lesson.

Other Vibrating Systems

As you know, bobblehead dolls are not the only objects that vibrate. It might be safe to say that all objects in one way or another can be forced to vibrate to some extent. The vibrations might not be large enough to be visible. Or the amount of damping might be so strong that the object scarcely completes a full cycle of vibration. But as long as a force persists to restore the object to its original position, a displacement from its 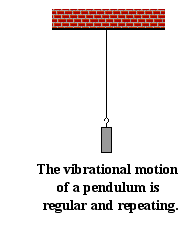resting position will result in a vibration. Even a large massive skyscraper is known to vibrate as winds push upon its structure. While held fixed in place at its foundation (we hope), the winds force the length of the structure out of position and the skyscraper is forced into vibration.

A pendulum is a classic example of an object that is considered to vibrate. A simple pendulum consists of a relatively massive object hung by a string from a fixed support. It typically hangs vertically in its equilibrium position. When the mass is displaced from equilibrium, it begins its back and forth vibration about its fixed equilibrium position. The motion is regular and repeating. In the next part of this lesson, we will describe such a regular and repeating motion as a periodic motion. Because of the regular nature of a pendulum's motion, many clocks, such as grandfather clocks, use a pendulum as part of its timing mechanism.

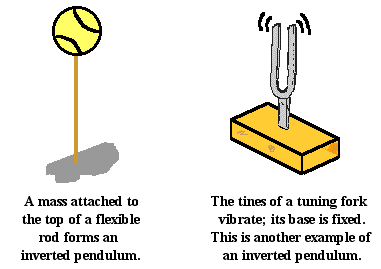
An inverted pendulum is another classic example of an object that undergoes vibrational motion. An inverted pendulum is simply a pendulum which has its fixed end located below the vibrating mass. An inverted pendulum can be made by attaching a mass (such as a tennis ball) to the top end of a dowel rod and then securing the bottom end of the dowel rod to a horizontal support. This is shown in the diagram below. A gentle force exerted upon the tennis ball will cause it to vibrate about a fixed, equilibrium position. The vibrating skyscraper can be thought of as a type of inverted pendulum. Tall trees are often displaced from their usual vertical orientation by strong winds. As the winds cease, the trees will vibrate back and forth about their fixed positions. Such trees can be thought of as acting as inverted pendula. Even the tines of a tuning fork can be considered a type of inverted pendulum

Another classic example of an object that undergoes vibrational motion is a mass on a spring. The animation at the right depicts a mass suspended 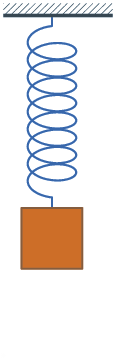from a spring. The mass hangs at a resting position. If the mass is pulled down, the spring is stretched. Once the mass is released, it begins to vibrate. It does the back and forth, vibrating about a fixed position. If the spring is rotated horizontally and the mass is placed upon a supporting surface, the same back and forth motion can be observed. Pulling the mass to the right of its resting position stretches the spring. When released, the mass is pulled back to the left, heading towards its resting position. After passing by its resting position, the spring begins to compress. The compressions of the coiled spring result in a restoring force that again pushes rightward on the leftward moving mass. The cycle continues as the mass vibrates back and forth about a fixed position. The springs inside of a bed mattress, the suspension systems of some cars, and bathroom scales all operated as a mass on a spring system.

In all the vibrating systems just mentioned, damping is clearly evident. The simple pendulum doesn't vibrate forever; its energy is gradually dissipated through air resistance and loss of energy to the support. The inverted pendulum consisting of a tennis ball mounted to the top of a dowel rod does not vibrate forever. Like the simple pendulum, the energy of the tennis ball is dissipated through air resistance and vibrations of the support. Frictional forces also cause the mass on a spring to lose its energy to the surroundings. In some instances, damping is a favored feature. Car suspension systems are intended to dissipate vibrational energy, preventing drivers and passengers from having to do the back and forth as they also do the down the road.

Hopefully a lot of our original questions have been answered. But one question that has not yet been answered is the question pertaining to quantities that can be measured. How can we quantitatively describe a vibrating object? What measurements can be made of vibrating objects that would distinguish one vibrating object from another? We will ponder this question on vibrational motion.