Power: Putting Charges to Work
Electric circuits are designed to serve a useful function.
The mere movement of charge from terminal to
terminal is
of little use if the electrical energy possessed by the charge is not
transformed into another useful form. To equip a circuit with a battery and a
wire leading from positive to negative terminal without an electrical device
(light bulb, beeper, motor, etc.) would lead to a high rate of charge flow.
Such a circuit is referred to as a short
circuit. With charge flowing rapidly between terminals, the rate at which
energy would be consumed would be high. Such a circuit would heat the wires to
a high temperature and drain the battery of its energy rather quickly. When a
circuit is equipped with a light bulb, beeper, or motor, the electrical energy
supplied to the charge by the battery is transformed into other forms in the
electrical device. A light bulb, beeper and motor are generally referred to as
a load. In a light bulb, electrical energy is
transformed into useful light energy (and some non-useful thermal energy). In a
beeper, electrical energy is transformed into sound energy. And in a motor,
electrical energy is transformed into mechanical energy.
An electrical circuit is simply an energy transformation
tool. Energy is provided to the circuit by an electrochemical cell, battery,
generator or other electrical energy source. And energy is delivered by the
circuit to the load at the location of the load. The rate at which this energy
transformation occurs is of great importance to those who design electrical
circuits for useful functions. Power - the rate at which mechanical work is done - was introduced in Unit 5 of the
Physics Classroom. Here, we will discuss power in electrical
terms; while the context has changed, the essential meaning of the concept of
power will remain the same. Power is the rate at which electrical energy is
supplied to a circuit or consumed by a load. The electrical energy is supplied
to the load by an energy source such as an electrochemical cell. Recall from Lesson 1 that a
cell does work upon a charge to move it from the low energy to the high energy
terminal. The work done on the charge is equivalent to the electrical potential
energy change of the charge. Thus, electrical power, like mechanical power, is
the rate at which work is done. Like current, power is a rate quantity. Its
mathematical formula is expressed on a per
time basis.
Whether the focus is the energy gained by the charge at the
energy source or the energy lost by the charge at the load, electrical power
refers to the rate at which the charge changes its 
energy. In an electrochemical cell (or other energy source), the change
is a positive change (i.e., a gain in energy) and at the load, the change is a
negative change (i.e., a loss in energy). Thus, power is often referred to as
the rate of energy change and its equation is expressed as the energy change
per time. Like mechanical power, the unit of electrical power is the watt, abbreviated W. (Quite obviously, it is important that the
symbol W as the unit of power not be confused with the symbol W for the
quantity of work done upon a charge by the energy source.) A watt of power is
equivalent to the delivery of 1 joule of energy every second. In other words:
1 watt = 1 joule / second
When it is observed that a light bulb is rated at 60 watts,
then there are 60 joules of energy delivered to the light bulb every second. A
120-watt light bulbs draws 120 joules of energy every second. The ratio of the
energy delivered or expended by the device to time is equal to the wattage of the device.
The
kilowatt-hour
Electrical utility companies who provide energy for homes
provide a monthly bill charging those homes for the electrical energy that they
used. A typical bill can be very complicated with a number of line items
indicating charges for various aspects of the utility service. But somewhere on
the bill will be a charge for the number of kilowatt-hours of electricity that were consumed. Exactly what is a
kilowatt-hour? Is it a unit of power? time? energy? or some other
quantity? And when we pay for the electricity that we use, what exactly is it
that we are paying for?
A careful inspection of the unit kilowatt-hour reveals the answers to these
questions. A kilowatt is a unit of power and an hour is a unit of time. So a 
kilowatt • hour is a unit of Power • time. If Power = ΔEnergy / time, then Power • time = ΔEnergy. So a unit of power • time
is a unit of energy. The kilowatt • hour is a unit of energy. When an
electrical utility company charges a household for the electricity that they
used, they are charging them for electrical energy. A utility company in the
United States is responsible for assuring that the electric potential
difference across the two main wires of the house is 110 to 120 volts. And
maintaining this difference in potential requires energy.
It is a common misconception that the utility company
provides electricity in the form of charge carriers or electrons. The fact is
that the mobile electrons that are in the wires of our homes would be there
whether there was a utility company or not. The electrons come with the atoms
that make up the wires of our household circuits. The utility company simply
provides the energy that causes the motion of the charge carriers within the
household circuits. And when they charge us for a few hundred kilowatt-hours of
electricity, they are providing us with an energy bill.
Investigate!
The electrical potential difference across the
two inserts of a household electrical outlet varies with the country. Use the Household
Voltages widget below to find out the household voltage values for
various countries (e.g., United States, Canada, Japan, China, South Africa,
etc.).
|
Household Voltages |
||
Calculating
Power
The rate at which energy is delivered to a light bulb by a
circuit is related to the electric potential difference established across the
ends of the circuit (i.e., the voltage rating of the energy source) and the
current flowing through the circuit. The relationship between power, current
and electric potential difference can be derived by combining the mathematical
definitions of power, electric potential difference and current. Power is the
rate at which energy is added to or removed from a circuit by a battery or a
load. Current is the rate at which charge moves past a point on a circuit. And
the electric potential difference across the two ends of a circuit is the
potential energy difference per charge between those two points. In equation
form, these definitions can be stated as
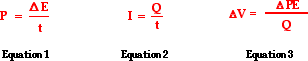
Equation 3 above can be rearranged to show that the energy
change across the two ends of a circuit is the product of the electric
potential difference and the charge - ΔV • Q. Substituting this expression
for energy change into Equation 1 will yield the following equation:
In the equation above, there is a Q in the
numerator and a t in the denominator. This is simply the current; and as such, the
equation can be rewritten as
The electrical power is simply the product of the electric
potential difference and the current. To determine the power of a battery or
other energy source (i.e., the rate at which it delivers energy to the
circuit), one simply takes the electric potential difference that it
establishes across the external circuit and multiplies it by the current in the
circuit. To determine the power of an electrical device or a load, one simply
takes the electric potential difference across the device (sometimes referred to
as the voltage drop) and multiplies it by the current in the device.
Check Your Understanding
1. The purpose of every circuit is to supply the energy to
operate various electrical devices. These devices are constructed to convert
the energy of flowing charge into other forms of energy (e.g., light, thermal,
sound, mechanical, etc.). Use complete sentences to describe the energy
conversions that occur in the following devices.
a.
Windshield wipers on a car
b. Defrosting circuit on a car
c. Hair dryer
a. Windshield wipers on a car: Electrical energy is converted
to mechanical energy.
b. Defrosting circuit on a car: Electrical energy is converted
to thermal energy.
c. Hair
dryer: Electrical
energy is converted to thermal and mechanical energy (and some useless sound
energy).
2. Determine the ...
a.
... current in a 60-watt bulb plugged into a 120-volt outlet.
b. ... current in a 120-watt bulb plugged into a 120-volt
outlet.
c. ... power of a saw that draws 12 amps of current when
plugged into a 120-volt outlet.
d. ... power of a toaster that draws 6 amps of current when
plugged into a 120-volt outlet.
e. ... current in a 1000-watt microwave when plugged into a
120-volt outlet.
For each problem, use the P = 
V • I
equation to solve for the unknown quantity. In a, b, and e, the unknown
quantity is current (I); and in c and d, the unknown quantity is power (P).
a. The current
in a 60-Watt bulb plugged into a 120-Volt outlet is 0.5 A.
I = P / V = (60 W) /
(120 V) = 0.5
A
b. The current in a 120-Watt bulb plugged into a 120-Volt outlet
is 1.0 A.
I = P / V = (120 W) /
(120 V) = 1.0
A
c. The power of a saw that draws 12 amps of current when plugged
into a 120-Volt outlet is 1440 W.
P = V • I = (120
V) • (12 A) = 1440 W
d. The power of a toaster that draws 6 amps of current when
plugged into a 120-Volt outlet is 720 W.
P = V • I = (120
V) • (6 A) = 720 W
e. The current in a 1000-Watt microwave when plugged into a
120-Volt outlet is 8.3 A.
I = P / V = (1000 W)
/ (120 V) = 8.3 A
3. Your 60-watt light bulb is plugged into a 110-volt
household outlet and left on for 3 hours. The utility company charges you $0.11
per kiloWatt•hr. Explain how you can calculate the cost of such a mistake.
The energy
consumed can be determined from knowledge of the power (60 Watts) and the time
(3 hrs). The energy consumed is 180 Watt•hr or
0.180 kW•hr. Each kW•hr costs
11 ˘ pr $0.11. Now simply multiply the cost
per ˘ by the amount of ˘ of energy consumed. The result is just a little short
of 2 cents.
4. Alfredo deDarke often leaves household appliances on for
no good reason (at least according to his parents). The deDarke family
pays 10˘/kilowatt-hour (i.e., $.10/kW•hr) for their electrical energy. Express your
understanding of the relationship between power, electrical energy, time, and
costs by filling in the table below.
|
Power Rating (Watt) |
Time (hrs) |
Energy Used (kilowatt-hour) |
Costs (cents) |
Costs ($) |
|
60 Watt Bulb |
1 |
0.060 kW•hr |
0.6 ˘ |
$0.006 |
|
60 Watt Bulb |
4 |
|
|
|
|
120 Watt Bulb |
2 |
|
|
|
|
100 Watt Bulb |
|
10 kW-hr |
|
|
|
60 Watt Bulb |
|
|
1000 ˘ |
$10 |
|
|
100 |
60 kW-hr |
|
|
The following relationships exist:
· The Power • time = Energy
Used. Units are important! The third column is expressed in kiloWatt•hour; thus it is important to convert the Watts
to kiloWatts. That is, the first column divided
by 1000 multiplied by the second column equals the third column.
· The cost in cents is equal
to the energy used (in kWhr) multiplied by 10 ˘
/ kWhr.
· The cost in dollars in
1/100-th the cost in cents.
|
Power Rating (Watt) |
Time (hrs) |
Energy Used (kilowatt-hour) |
Costs (cents) |
Costs ($) |
|
60 Watt Bulb |
1 |
0.060 kW•hr |
0.6 ˘ |
$ 0.006 |
|
60 Watt Bulb |
4 |
0.240 kW•hr |
2.4 ˘ |
$ 0.024 |
|
120 Watt Bulb |
2 |
0.240 kW•hr |
2.4 ˘ |
$ 0.024 |
|
100 Watt Bulb |
100 |
10 kW-hr |
100 ˘ |
$ 1.00 |
|
60 Watt Bulb |
1667 |
100 kW-hr |
1000 ˘ |
$10 |
|
600 Watt Bulb |
100 |
60 kW-hr |
600 ˘ |
$ 6 |