Combination Circuits

Previously in Lesson 4, it was mentioned that there are two different ways to connect two or more electrical devices together in a circuit. They can be connected by means of series connections or by means of parallel connections. When all the devices in a circuit are connected by series connections, then the circuit is referred to as a series circuit. When all the devices in a circuit are connected by 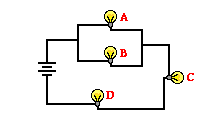http://www.physicsclassroom.com/Class/circuits/u9l4e1.webpparallel connections, then the circuit is referred to as a parallel circuit. A third type of circuit involves the dual use of series and parallel connections in a circuit; such circuits are referred to as compound circuits or combination circuits. The circuit depicted at the right is an example of the use of both series and parallel connections within the same circuit. In this case, light bulbs A and B are connected by parallel connections and light bulbs C and D are connected by series connections. This is an example of a combination circuit.

When analyzing combination circuits, it is critically important to have a solid understanding of the concepts that pertain to both series circuits and parallel circuits. Since both types of connections are used in combination circuits, the concepts associated with both types of circuits apply to the respective parts of the circuit. The main concepts associated with series and parallel circuits are organized in the table below.

Series Circuits

·         The current is the same in every resistor; this current is equal to that in the battery.

·         The sum of the voltage drops across the individual resistors is equal to the voltage rating of the battery.

·         The overall resistance of the collection of resistors is equal to the sum of the individual resistance values,

Rtot = R1 + R2 + R3 + ...

Parallel Circuits

·         The voltage drop is the same across each parallel branch.

·         The sum of the current in each individual branch is equal to the current outside the branches.

·         The equivalent or overall resistance of the collection of resistors is given by the equation

1/Req = 1/R1 + 1/R2 + 1/R3 ...

Each of the above concepts has a mathematical expression. Combining the mathematical expressions of the above concepts with the Ohm's law equation (ΔV = I • R) allows one to conduct a complete analysis of a combination circuit.

 

Analysis of Combination Circuits

The basic strategy for the analysis of combination circuits involves using the meaning of equivalent resistance for parallel branches to transform the combination circuit into a series circuit. Once transformed into a series circuit, the analysis can be conducted in the usual manner. Previously in Lesson 4, the method for determining the equivalent resistance of parallel are equal, then the total or equivalent resistance of those branches is equal to the resistance of one branch divided by the number of branches.

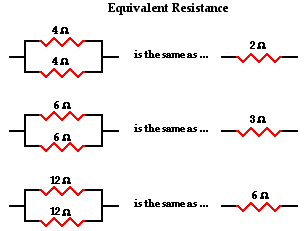
http://www.physicsclassroom.com/Class/circuits/u9l4d4.webp

This method is consistent with the formula

 

1 / Req = 1 / R1 + 1 / R2 + 1 / R3 + ...

where R1, R2, and R3 are the resistance values of the individual resistors that are connected in parallel. If the two or more resistors found in the parallel branches do not have equal resistance, then the above formula must be used. An example of this method was presented in a previous section of Lesson 4.

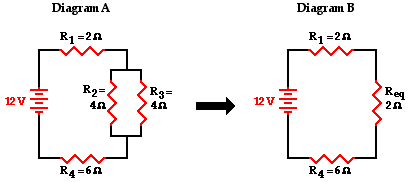
By applying one's understanding of the equivalent resistance of parallel branches to a combination circuit, the combination circuit can be transformed into a series circuit. Then an understanding of the equivalent resistance of a series circuit can be used to determine the total resistance of the circuit. Consider the following diagrams below. Diagram A represents a combination circuit with resistors R2 and R3 placed in parallel branches. Two 4-Ω resistors in parallel is equivalent to a resistance of 2 Ω. Thus, the two branches can be replaced by a single resistor with a resistance of 2 Ω. This is shown in Diagram B. Now that all resistors are in series, the formula for the total resistance of series resistors can be used to determine the total resistance of this circuit: The formula for series resistance is

 

Rtot = R1 + R2 + R3 + ...

So in Diagram B, the total resistance of the circuit is 10 Ω.

http://www.physicsclassroom.com/Class/circuits/u9l4e2.webp

Once the total resistance of the circuit is determined, the analysis continues using Ohm's law and voltage and resistance values to determine current values at various locations. The entire method is illustrated below with two examples.

 

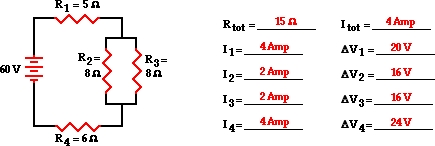
Example 1:

The first example is the easiest case - the resistors placed in parallel have the same resistance. The goal of the analysis is to determine the current in and the voltage drop across each resistor.

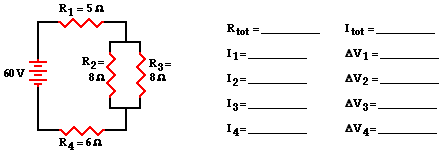
http://www.physicsclassroom.com/Class/circuits/u9l4e3.webp

As discussed above, the first step is to simplify the circuit by replacing the two parallel resistors with a single resistor that has an equivalent resistance. Two 8 Ω resistors in series is equivalent to a single 4 Ω resistor. Thus, the two branch resistors (R2 and R3) can be replaced by a single resistor with a resistance of 4 Ω. This 4 Ω resistor is in series with R1 and R4. Thus, the total resistance is

Rtot = R1 + 4 Ω + R4 = 5 Ω + 4 Ω + 6 Ω

Rtot = 15 Ω

Now the Ohm's law equation (ΔV = I • R) can be used to determine the total current in the circuit. In doing so, the total resistance and the total voltage (or battery voltage) will have to be used.

Itot = ΔVtot / Rtot = (60 V) / (15 Ω)

Itot = 4 Amp

The 4 Amp current calculation represents the current at the battery location. Yet, resistors R1 and R4 are in series and the current in series-connected resistors is everywhere the same. Thus,

Itot = I1 = I4 = 4 Amp

For parallel branches, the sum of the current in each individual branch is equal to the current outside the branches. Thus, I2 + I3 must equal 4 Amp. There are an infinite number of possible values of I2 and I3 that satisfy this equation. Since the resistance values are equal, the current values in these two resistors are also equal. Therefore, the current in resistors 2 and 3 are both equal to 2 Amp.

I2 = I3 = 2 Amp

Now that the current at each individual resistor location is known, the Ohm's law equation (ΔV = I • R) can be used to determine the voltage drop across each resistor. These calculations are shown below.

ΔV1 = I1 • R1 = (4 Amp) • (5 Ω)

ΔV1 = 20 V

ΔV2 = I2 • R2 = (2 Amp) • (8 Ω)

ΔV2 = 16 V

ΔV3 = I3 • R3 = (2 Amp) • (8 Ω)

ΔV3 = 16 V

ΔV4 = I4 • R4 = (4 Amp) • (6 Ω)

ΔV4 = 24 V

 

The analysis is now complete and the results are summarized in the diagram below.

http://www.physicsclassroom.com/Class/circuits/u9l4e4.webp

 

 

Example 2:

The second example is the more difficult case - the resistors placed in parallel have a different resistance value. The goal of the analysis is the same - to determine the current in and the voltage drop across each resistor.

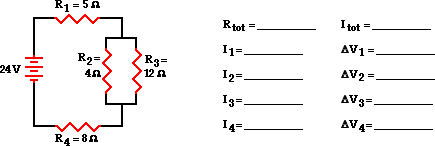
 http://www.physicsclassroom.com/Class/circuits/u9l4e5.webp

As discussed above, the first step is to simplify the circuit by replacing the two parallel resistors with a single resistor with an equivalent resistance. The equivalent resistance of a 4-Ω and 12-Ω resistor placed in parallel can be determined using the usual formula for equivalent resistance of parallel branches:

1 / Req = 1 / R1 + 1 / R2 + 1 / R3 ...

1 / Req = 1 / (4 Ω) + 1 / (12 Ω)

1 / Req = 0.333 Ω-1

Req = 1 / (0.333 Ω-1)

Req = 3.00 Ω

Based on this calculation, it can be said that the two branch resistors (R2 and R3) can be replaced by a single resistor with a resistance of 3 Ω. This 3 Ω resistor is in series with R1 and R4. Thus, the total resistance is

Rtot = R1 + 3 Ω + R4 = 5 Ω + 3 Ω + 8 Ω

Rtot = 16 Ω

Now the Ohm's law equation (ΔV = I • R) can be used to determine the total current in the circuit. In doing so, the total resistance and the total voltage (or battery voltage) will have to be used.

Itot = ΔVtot / Rtot = (24 V) / (16 Ω)

Itot = 1.5 Amp

The 1.5 Amp current calculation represents the current at the battery location. Yet, resistors R1 and R4 are in series and the current in series-connected resistors is everywhere the same. Thus,

Itot = I1 = I4 = 1.5 Amp

For parallel branches, the sum of the current in each individual branch is equal to the current outside the branches. Thus, I2 + I3 must equal 1.5 Amp. There are an infinite possibilities of I2 and I3 values that satisfy this equation. In the previous example, the two resistors in parallel had the identical resistance; thus the current was distributed equally among the two branches. In this example, the unequal current in the two resistors complicates the analysis. The branch with the least resistance will have the greatest current. Determining the amount of current will demand that we use the Ohm's law equation. But to use it, the voltage drop across the branches must first be known. So the direction that the solution takes in this example will be slightly different than that of the simpler case illustrated in the previous example.

To determine the voltage drop across the parallel branches, the voltage drop across the two series-connected resistors (R1 and R4) must first be determined. The Ohm's law equation (ΔV = I • R) can be used to determine the voltage drop across each resistor. These calculations are shown below.

ΔV1 = I1 • R1 = (1.5 Amp) • (5 Ω)

ΔV1 = 7.5 V

ΔV4 = I4 • R4 = (1.5 Amp) • (8 Ω)

ΔV4 = 12 V

This circuit is powered by a 24-volt source. Thus, the cumulative voltage drop of a charge traversing a loop about the circuit is 24 volts. There will be a 19.5 V drop (7.5 V + 12 V) resulting from passage through the two series-connected resistors (R1 and R4). The voltage drop across the branches must be 4.5 volts to make up the difference between the 24 volt total and the 19.5-volt drop across R1 and R4. Thus,

ΔV2 = http://www.physicsclassroom.com/Class/circuits/rdbddelta.webpV3 = 4.5 V

Knowing the voltage drop across the parallel-connected resistors (R1 and R4) allows one to use the Ohm's law equation (ΔV = I • R) to determine the current in the two branches.

I2 = ΔV2 / R2 = (4.5 V) / (4 Ω)

I2 = 1.125 A

I3 = ΔV3 / R3 = (4.5 V) / (12 Ω)

I3 = 0.375 A

The analysis is now complete and the results are summarized in the diagram below.

http://www.physicsclassroom.com/Class/circuits/u9l4e6.webp

 

 

Developing a Strategy

The two examples above illustrate an effective concept-centered strategy for analyzing combination circuits. The approach demanded a firm grasp of the series and parallel concepts discussed earlier. Such analyses are often conducted in order to solve a physics problem for a specified unknown. In such situations, the unknown typically varies from problem to problem. In one problem, the resistor values may be given and the current in all the branches are the unknown. In another problem, the current in the battery and a few resistor values may be stated and the unknown quantity becomes the resistance of one of the resistors. Different problem situations will obviously require slight alterations in the approaches. Nonetheless, every problem-solving approach will utilize the same principles utilized in approaching the two example problems above.

The following suggestions for approaching combination circuit problems are offered to the beginning student:

·         If a schematic diagram is not provided, take the time to construct one. Use schematic symbols such as those shown in the example above.

·         When approaching a problem involving a combination circuit, take the time to organize yourself, writing down known values and equating them with a symbol such as Itot, I1, R3, ΔV2, etc. The organization scheme used in the two examples above is an effective starting point.

·         Know and use the appropriate formulae for the equivalent resistance of series-connected and parallel-connected resistors. Use of the wrong formulae will guarantee failure.

·         Transform a combination circuit into a strictly series circuit by replacing (in your mind) the parallel section with a single resistor having a resistance value equal to the equivalent resistance of the parallel section.

·         Use the Ohm's law equation (ΔV = I • R) often and appropriately. Most answers will be determined using this equation. When using it, it is important to substitute the appropriate values into the equation. For instance, if calculating I2, it is important to substitute the ΔV2 and the R2 values into the equation.

For further practice analyzing combination circuits, consider analyzing the problems in the Check Your Understanding section below

 

Check Your Understanding

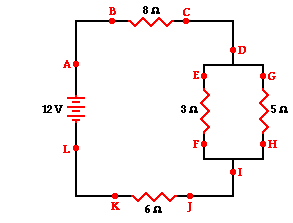http://www.physicsclassroom.com/Class/circuits/u9l4e7.webp1. A combination circuit is shown in the diagram at the right. Use the diagram to answer the following questions.

a. The current at location A is _____ (greater than, equal to, less than) the current at location B.

b. The current at location B is _____ (greater than, equal to, less than) the current at location E.

c. The current at location G is _____ (greater than, equal to, less than) the current at location F.

d. The current at location E is _____ (greater than, equal to, less than) the current at location G.

e. The current at location B is _____ (greater than, equal to, less than) the current at location F.

f. The current at location A is _____ (greater than, equal to, less than) the current at location L.

g. The current at location H is _____ (greater than, equal to, less than) the current at location I.

See Answer

 http://www.physicsclassroom.com/Class/circuits/cyuAnswers/cyuheader.webp

The current outside the branches of a combination circuit is everywhere the same. The current inside of the branches is always less than that outside of the branches. When comparing the current of two parallel-connected resistors, the resistor with the least resistance will have the greatest current. The current within a single branch will be the same above and below the resistor.

http://www.physicsclassroom.com/Class/circuits/cyuAnswers/u9l4e7.webpa. The current at location A is equal to the current at location B.

b. The current at location B is greater than the current at location E.

c. The current at location G is less than the current at location F.

d. The current at location E is greater than the current at location G.

e. The current at location B is greater than the current at location F.

f. The current at location A is equal to the current at location L.

g. The current at location H is less than the current at location I.

 

 

 

http://www.physicsclassroom.com/Class/circuits/u9l4e7.webp2. Consider the combination circuit in the diagram at the right. Use the diagram to answer the following questions. (Assume that the voltage drops in the wires themselves in negligibly small.)

a. The electric potential difference (voltage drop) between points B and C is _____ (greater than, equal to, less than) the electric potential difference (voltage drop) between points J and K.

b. The electric potential difference (voltage drop) between points B and K is _____ (greater than, equal to, less than) the electric potential difference (voltage drop) between points D and I.

c. The electric potential difference (voltage drop) between points E and F is _____ (greater than, equal to, less than) the electric potential difference (voltage drop) between points G and H.

d. The electric potential difference (voltage drop) between points E and F is _____ (greater than, equal to, less than) the electric potential difference (voltage drop) between points D and I.

e. The electric potential difference (voltage drop) between points J and K is _____ (greater than, equal to, less than) the electric potential difference (voltage drop) between points D and I.

f. The electric potential difference between points L and A is _____ (greater than, equal to, less than) the electric potential difference (voltage drop) between points B and K.

  

See Answer

 http://www.physicsclassroom.com/Class/circuits/cyuAnswers/cyuheader.webp

The voltage drop across a resistor is dependent upon the current in the resistor and the resistance of the resistor. In situations in which the current is the same for both resistors (such as for series-connected resistors), the resistor with the greatest resistance will have the greatest voltage drop.

http://www.physicsclassroom.com/Class/circuits/cyuAnswers/u9l4e7.webpa. The electric potential difference (voltage drop) between points B and C is greater than the electric potential difference (voltage drop) between points J and K.

b. The electric potential difference (voltage drop) between points B and K is greater than the electric potential difference (voltage drop) between points D and I.

c. The electric potential difference (voltage drop) between points E and F is equal to the electric potential difference (voltage drop) between points G and H.

d. The electric potential difference (voltage drop) between points E and F is equal to the electric potential difference (voltage drop) between points D and I.

e. The electric potential difference (voltage drop) between points J and K is greater than the electric potential difference (voltage drop) between points D and I.

f. The electric potential difference between points L and A is equal to the electric potential difference (voltage drop) between points B and K.

close

 


 

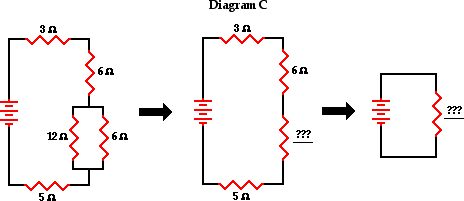
3. Use the concept of equivalent resistance to determine the unknown resistance of the identified resistor that would make the circuits equivalent.

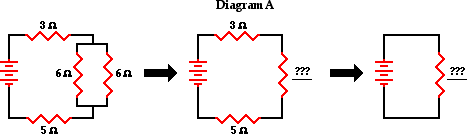
http://www.physicsclassroom.com/Class/circuits/u9l4e8.webp

See Answer

http://www.physicsclassroom.com/Class/circuits/cyuAnswers/cyuheader.webp

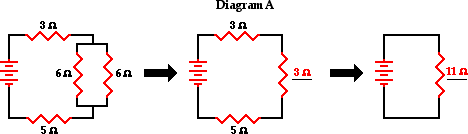
http://www.physicsclassroom.com/Class/circuits/cyuAnswers/l4eq3a.webp

For parallel-connected resistors:

1/Req = 1/R1 + 1/R2 = 1 / (6 http://www.physicsclassroom.com/Class/circuits/cyuAnswers/omegablack.webp) + 1 / (6 http://www.physicsclassroom.com/Class/circuits/cyuAnswers/omegablack.webp) = 2 / (6 http://www.physicsclassroom.com/Class/circuits/cyuAnswers/omegablack.webp)

Req = 3 http://www.physicsclassroom.com/Class/circuits/cyuAnswers/omegablack.webp

For series-connected resistors:

Req = R1 + R2 + R3 = 3 http://www.physicsclassroom.com/Class/circuits/cyuAnswers/omegablack.webp + 3 http://www.physicsclassroom.com/Class/circuits/cyuAnswers/omegablack.webp + 5 http://www.physicsclassroom.com/Class/circuits/cyuAnswers/omegablack.webp

Req = 11 http://www.physicsclassroom.com/Class/circuits/cyuAnswers/omegablack.webp


 

 

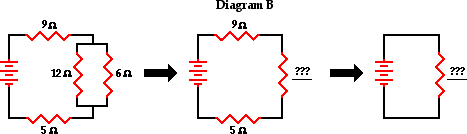
http://www.physicsclassroom.com/Class/circuits/u9l4e9.webp

See Answer

http://www.physicsclassroom.com/Class/circuits/cyuAnswers/cyuheader.webp

http://www.physicsclassroom.com/Class/circuits/cyuAnswers/l4eq3b.webp

 

For parallel-connected resistors:

1/Req = 1/R1 + 1/R2 = 1 / (12 http://www.physicsclassroom.com/Class/circuits/cyuAnswers/omegablack.webp) + 1 / (6 http://www.physicsclassroom.com/Class/circuits/cyuAnswers/omegablack.webp) = 3 / (12 http://www.physicsclassroom.com/Class/circuits/cyuAnswers/omegablack.webp)

Req = 4 http://www.physicsclassroom.com/Class/circuits/cyuAnswers/omegablack.webp

For series-connected resistors:

Req = R1 + R2 + R3 = 9 http://www.physicsclassroom.com/Class/circuits/cyuAnswers/omegablack.webp + 4 http://www.physicsclassroom.com/Class/circuits/cyuAnswers/omegablack.webp + 5 http://www.physicsclassroom.com/Class/circuits/cyuAnswers/omegablack.webp

Req = 18 http://www.physicsclassroom.com/Class/circuits/cyuAnswers/omegablack.webp


 

 

http://www.physicsclassroom.com/Class/circuits/u9l4e10.webp

See Answer

 http://www.physicsclassroom.com/Class/circuits/cyuAnswers/cyuheader.webp

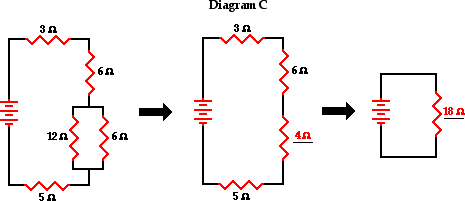
http://www.physicsclassroom.com/Class/circuits/cyuAnswers/l4eq3c.webp

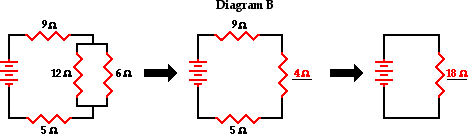
For parallel-connected resistors:

1/Req = 1/R1 + 1/R2 = 1 / (12 Ω) + 1 / (6 Ω) = 3 / (12 Ω)

Req = 4 Ω

For series-connected resistors:

Req = R1 + R2 + R3 + R4 = 3 Ω + 6 Ω + 4 Ω + 5 Ω

Req = 18 Ω

 


 

4. Analyze the following circuit and determine the values of the total resistance, total current, and the current at and voltage drops across each individual resistor.

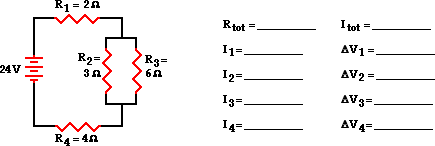
http://www.physicsclassroom.com/Class/circuits/u9l4e11.webp

See Answer

 

http://www.physicsclassroom.com/Class/circuits/cyuAnswers/cyuheader.webp

http://www.physicsclassroom.com/Class/circuits/cyuAnswers/l4eq4.webp

The first step is to simplify the circuit by replacing the two parallel resistors with a single resistor with an equivalent resistance. The equivalent resistance of a 4 Ω and 6 Ω resistor placed in parallel can be determined using the usual formula for equivalent resistance of parallel branches:

1 / Req = 1 / R1 + 1 / R2 + 1 / R3 ...

1 / Req = 1 / (3 Ω) + 1 / (6 Ω)

1 / Req = 0.500 Ω-1

Req = 1 / (0.500 Ω-1)

Req = 2.00 Ω

Based on this calculation, it can be said that the two branch resistors (R2 and R3) can be replaced by a single resistor with a resistance of 2 Ω. This 2 Ω resistor is in series with R1 and R4. Thus, the total resistance is

Rtot = R1 + 2 Ω + R4 = 2 Ω + 2 Ω + 4 Ω

Rtot = 8 Ω

Now the Ohm's law equation (ΔV = I • R) can be used to determine the total current in the circuit. In doing so, the total resistance and the total voltage (or battery voltage) will have to be used.

Itot = ΔVtot / Rtot = (24 V) / (8 http://www.physicsclassroom.com/Class/circuits/cyuAnswers/omegablack.webp)

Itot = 3.0 Amp

The 3.0 Amp current calculation represents the current at the battery location. Yet, resistors R1 and R4 are in series and the current in series-connected resistors is everywhere the same. Thus,

Itot = I1 = I4 = 3.0 Amp

For parallel branches, the sum of the current in each individual branch is equal to the current outside the branches. Thus, I2 + I3 must equal 3.0 Amp. There are an infinite possibilities of I2 and I3 values which satisfy this equation. Determining the amount of current in either branch will demand that we use the Ohm's law equation. But to use it, the voltage drop across the branches must first be known. To determine the voltage drop across the parallel branches, the voltage drop across the two series-connected resistors (R1 and R4) must first be determined. The Ohm's law equation (ΔV = I • R) can be used to determine the voltage drop across each resistor. These calculations are shown below.

ΔV1 = I1 • R1 = (3.0 Amp) • (2 http://www.physicsclassroom.com/Class/circuits/cyuAnswers/omegablack.webp) = 6.0 V
Δ

V4 = I4 • R4 = (3.0 Amp) • (4 http://www.physicsclassroom.com/Class/circuits/cyuAnswers/omegablack.webp) = 12 V

This circuit is powered by a 24-volt source. Thus, the cumulative voltage drop of a charge traversing a loop about the circuit is 24 volts. There will be a 18.0 V drop (6.0 V + 12.0 V) resulting from passage through the two series-connected resistors (R1 and R4). The voltage drop across the branches must be 6.0 volts to make up the difference between the 24 volt total and the 18.0 volt drop across R1 and R4. Knowing the voltage drop across the parallel-connected resistors (R1 and R4) allows one to use the Ohm's law equation (ΔV = I • R) to determine the current in the two branches.

I2 = ΔV2 / R2 = (6.0 V) / (3 http://www.physicsclassroom.com/Class/circuits/cyuAnswers/omegablack.webp) = 2.0 A

I3 = ΔV3 / R3 = (6.0 V) / (6 http://www.physicsclassroom.com/Class/circuits/cyuAnswers/omegablack.webp) = 1.0 A


 

 

5. Referring to the diagram in question #4, determine the ...

a. ... power rating of resistor 4.

b. ... rate at which energy is consumed by resistor 3.

See Answer

 http://www.physicsclassroom.com/Class/circuits/cyuAnswers/cyuheader.webp

The power rating of a resistor can be determined from any one of the following formulae:

P = I • ΔV

P = I2 • R

P = ΔV 2 / R

Since all three variables (I, ΔV and R) are known, either one of the equations can be used to calculate power.

a. P4 = I4 • ΔV4 = (3 A) • (12 V) = 36.0 Watt

b. P3 = I3 • ΔV3 = (1 A) • (6 V) = 6.0 Watt