Parallel Circuits
As mentioned in a previous section of Lesson 4, two or more electrical devices in a circuit can be connected by series
connections or by parallel connections. When all the devices are connected
using parallel connections, the circuit is referred to 
as a parallel circuit. In a parallel circuit, each
device is placed in its own separate branch. The presence of
branch lines means that there are multiple pathways by which charge can
traverse the external circuit. Each charge passing through the loop of the
external circuit will pass through a single resistor present in a single
branch. When arriving at the branching location or node, a charge makes a
choice as to which branch to travel through on its journey back to the low
potential terminal.
A short comparison and contrast between series and parallel
circuits was made in an earlier section of Lesson 4. In that section, it was emphasized that the act of adding more
resistors to a parallel circuit results in the rather unexpected result of
having less overall resistance. Since there are multiple pathways by which
charge can flow, adding another resistor in a separate branch provides another
pathway by which to direct charge through the main area of resistance within
the circuit. This decreased resistance resulting from increasing the number of
branches will have the effect of increasing the rate at which charge flows
(also known as the current). In an effort to make this rather unexpected result
more reasonable, a tollway analogy was
introduced. A tollbooth is the main location of resistance to car flow on a
tollway. Adding additional tollbooths within their own branch on a tollway will
provide more pathways for cars to flow through the toll station. These
additional tollbooths will decrease the overall resistance to car flow and
increase the rate at which they flow.
Current
The rate at which charge flows through a circuit is known as
the current. Charge does NOT pile up and begin to
accumulate at any given location such that the current at one location is more
than at other locations. Charge does NOT become used up by resistors in such a
manner that there is less current at one location compared to another. In a
parallel circuit, charge divides up into
separate branches such that there can be more current in one branch than there
is in another. Nonetheless, when taken as a whole, the total amount of current
in all the branches when added together is the same as the amount of current at
locations outside the branches. The rule that current is
everywhere the same still works, only with a twist. The current
outside the branches is the same as the sum of the current in the individual
branches. It is still the same amount of current, only split up into more than
one pathway.
In equation form, this principle can be written as
Itotal =
I1 + I2 + I3 + ...
where Itotal is the
total amount of current outside the branches (and in the battery) and I1,
I2, and I3represent the current in the individual
branches of the circuit.
Throughout this unit, there has been an extensive reliance
upon the analogy between charge flow and water flow. Once more, we will return
to the analogy to illustrate how the sum of the current values in the branches
is equal to the amount outside of the branches. The flow of charge in wires is
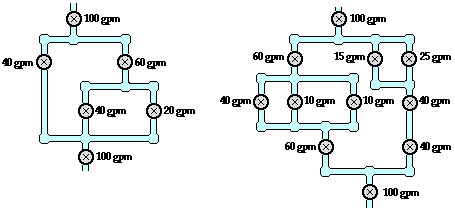
analogous to the flow of water in pipes. Consider the diagrams below in which
the flow of water in pipes becomes divided into separate branches. At each node (branching
location), the water takes two or more separate pathways. The rate at which
water flows into the node (measured in gallons per minute) will be equal to the
sum of the flow rates in the individual branches beyond the node. Similarly,
when two or more branches feed into a node, the rate at which water flows out
of the node will be equal to the sum of the flow rates in the individual
branches that feed into the node.
The same principle of flow division applies to electric
circuits. The rate at which charge flows into a
node is equal to the sum of the flow rates in the individual branches
beyond the node. This is illustrated in the examples shown below. In the
examples a new circuit symbol is introduced - the letter A enclosed within a
circle. This is the symbol for an ammeter - a device used to measure the current
at a specific point. An ammeter is capable of measuring the current while
offering negligible resistance to the flow of charge.
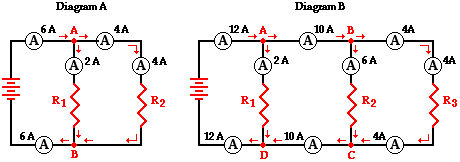
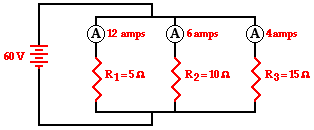
Diagram A displays two
resistors in parallel with nodes at point A and point B. Charge flows into
point A at a rate of 6 amps and divides into two pathways - one through
resistor 1 and the other through resistor 2. The current in the branch with
resistor 1 is 2 amps and the current in the branch with resistor 2 is 4 amps.
After these two branches meet again at point B to form a single line, the
current again becomes 6 amps. Thus we see the principle that the current
outside the branches is equal to the sum of the current in the individual
branches holds true.
Itotal =
I1 + I2
6 amps = 2 amps + 4 amps
Diagram B above may be slightly more complicated with its
three resistors placed in parallel. Four nodes are identified on the diagram
and labeled A, B, C and D. Charge flows into point A at a rate of 12 amps and
divides into two pathways - one passing through resistor 1 and the other
heading towards point B (and resistors 2 and 3). The 12 amps of current is
divided into a 2 amp pathway (through resistor 1) and a 10 amp pathway (heading
toward point B). At point B, there is further division of the flow into two
pathways - one through resistor 2 and the other through resistor 3. The current
of 10 amps approaching point B is divided into a 6-amp pathway (through
resistor 2) and a 4-amp pathway (through resistor 3). Thus, it is seen that the
current values in the three branches are 2 amps, 6 amps and 4 amps and that the
sum of the current values in the individual branches is equal to the current
outside the branches.
Itotal =
I1 + I2 + I3
12 amps = 2 amps + 6 amps + 4 amps
A flow analysis at points C and D can also be conducted and
it is observed that the sum of the flow rates heading into these points is
equal to the flow rate that is found immediately beyond these points.
Equivalent
Resistance
The actual amount of current always varies inversely with the
amount of overall resistance. There is a clear relationship between the
resistance of the individual resistors and the overall resistance of the
collection of resistors. To explore this relationship, let's begin with the
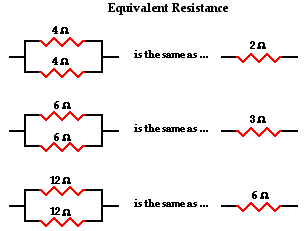
simplest case of two resistors placed in parallel branches, each having the
same resistance value of 4 Ω. Since the circuit offers two equalpathways for charge flow, only one-half the charge will choose to pass
through a given branch. While each individual branch offers 4 Ω of
resistance to any charge that flows through it, only one-half of all the charge
flowing through the circuit will encounter the 4 Ω resistance of that
individual branch. Thus, as far as the battery that is pumping the charge is
concerned, the presence of two 4-Ω resistors in parallel would be
equivalent to having one 2-Ω resistor in the circuit. In the same manner,
the presence of two 6-Ω resistors in parallel would be equivalent to
having one 3-Ω resistor in the circuit. And the presence of two 12-Ω
resistors in parallel would be equivalent to having one 6-Ω resistor in
the circuit.
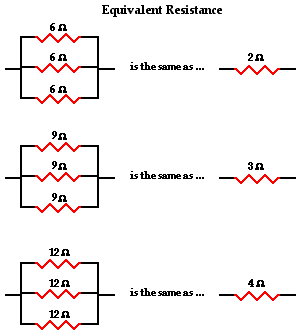
Now let's consider another simple case of having three
resistors in parallel, each having the same resistance of 6 Ω. With three equal pathways
for charge to flow through the external circuit, only one-third the charge will
choose to pass through a given branch. Each individual branch offers 6 Ω
of resistance to the charge that passes through it. However, the fact that only
one-third of the charge passes through a particular branch means that the
overall resistance of the circuit is 2 Ω. As far as the battery that is
pumping the charge is concerned, the presence of three 6-Ω resistors in
parallel would be equivalent to having one 2-Ω resistor in the circuit. In
the same manner, the presence of three 9-Ω resistors in parallel would be
equivalent to having one 3-Ω resistor in the circuit. And the presence of
three 12-Ω resistors in parallel would be equivalent to having one 4-Ω
resistor in the circuit.
This is the concept of equivalent resistance. The equivalent
resistance of a circuit is the amount of resistance that a single resistor would
need in order to equal the overall effect of the collection of resistors that
are present in the circuit. For parallel circuits, the mathematical formula for
computing the equivalent resistance (Req) is
1 / Req =
1 / R1 + 1 / R2 + 1 / R3 + ...
where R1,
R2, and R3 are the resistance values of the individual
resistors that are connected in parallel. The examples above could be
considered simple cases in which all the pathways offer the same amount of
resistance to an individual charge that passes through it. The simple cases
above were done without the use of the equation. Yet the equation fits both the
simple cases where branch resistors have the same resistance values and the
more difficult cases where branch resistors have different resistance values.
For instance, consider the application of the equation to the one simple and
one difficult case below.
Voltage
Drops for Parallel Branches
It has been emphasized throughout the Circuits
unit of The Physics Classroom tutorial that whatever voltage boost is
acquired by a charge in the battery is lost by the charge as it passes through
the resistors of the external circuit. The total voltage drop in the external
circuit is equal to the gain in voltage as a charge passes through the internal
circuit. In a parallel circuit, a charge does not pass through every resistor;
rather, it passes through a single resistor. Thus, the entire voltage drop
across that resistor must match the battery voltage. It matters not whether the
charge passes through resistor 1, resistor 2, or resistor 3, the voltage drop
across the resistor that it chooses to pass
through must equal the voltage of the battery. Put in equation form, this
principle would be expressed as
Vbattery = V1 = V2 = V3 = ...
If three resistors are placed in parallel branches and
powered by a 12-volt battery, then the voltage drop across each one of the
three resistors is 12 volts. A charge flowing through the circuit would only
encounter one of these three resistors and thus encounter a single voltage drop
of 12 volts.
Electric potential diagrams were introduced
in Lesson 1 of this unit and subsequently used to illustrate the consecutive voltage
drops occurring in series circuits. An
electric potential diagram is a conceptual tool for representing the electric
potential difference between several points on an electric circuit. Consider
the circuit diagram below and its corresponding electric potential diagram.
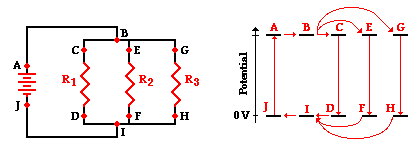
As shown in the electric potential diagram, positions A, B,
C, E and G are all at a high electric potential. A single charge chooses only one
of the three possible pathways; thus at position B, a single charge will move
towards point C, E or G and then passes through the resistor that is in that
branch. The charge does not lose its high potential until it passes through the
resistor, either from C to D, E to F, or G to H. Once it passes through a
resistor, the charge has returned to nearly 0 Volts and returns to the negative
terminal of the battery to obtain its voltage boost. Unlike in series circuits,
a charge in a parallel circuit encounters a single voltage drop during its path
through the external circuit.
The current through a given branch can be predicted using the
Ohm's law equation and the voltage drop across the resistor and the resistance
of the resistor. Since the voltage drop is the same across each resistor, the
factor that determines that resistor has the greatest current is the
resistance. The resistor with the greatest resistance experiences the lowest
current and the resistor with the least resistance experiences the greatest
current. In this sense, it could be said that charge (like people) chooses the path
of least resistance. In equation form, this could be stated as
|
I1 = ΔV1 / R1 |
I2 = ΔV2 / R2 |
I3 = ΔV3 / R3 |
This principle is illustrated by the circuit shown below. The
product of I•R is the same for each resistor (and equal to the battery
voltage). Yet the current is different in each resistor. The current is
greatest where the resistance is least and the current is least where the
resistance is greatest.
Mathematical Analysis of Parallel Circuits
The above principles and formulae can be used to analyze a
parallel circuit and determine the values of the current at and electric
potential difference across each of the resistors in a parallel circuit. Their
use will be demonstrated by the mathematical analysis of the circuit shown
below. The goal is to use the formulae to determine the equivalent resistance
of the circuit (Req), the current through the battery (Itot),
and the voltage drops and current for each of the three resistors.
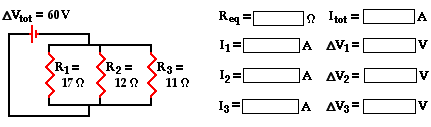
The analysis begins by using the resistance values for the
individual resistors in order to determine the equivalent resistance of the
circuit.
1 / Req =
1 / R1 + 1 / R2 + 1 / R3 = (1 / 17 Ω) + (1 / 12 Ω) +
(1 / 11 Ω)
1 / Req = 0.23306 Ω-1
Req = 1 / (0.23306 Ω-1)
Req = 4.29 Ω
(rounded from 4.29063 Ω)
Now that the equivalent resistance is known, the current in
the battery can be determined using the Ohm's law equation. In using the Ohm's
law equation (ΔV = I • R) to determine the current in the battery, it is
important to use the battery voltage for ΔV and the equivalent resistance
for R. The calculation is shown here:
Itot = ΔVbattery / Req = (60 V) / (4.29063 Ω)
Itot = 14.0 amp
(rounded from 13.98396 amp)
The 60 V battery voltage represents the gain in electric
potential by a charge as it passes through the battery. The charge loses this
same amount of electric potential for any given pass through the external
circuit. That is, the voltage drop across each one of the three resistors is
the same as the voltage gained in the battery:
ΔV battery = ΔV1 = ΔV2 = ΔV3 = 60 V
There are three values left to be determined - the current in
each of the individual resistors. Ohm's law is used once more to determine the
current values for each resistor - it is simply the voltage drop across each
resistor (60 Volts) divided by the resistance of each resistor (given in the
problem statement). The calculations are shown below.
|
I1 = ΔV1 / R1 I1 = (60 V) / (17 Ω) I1 = 3.53 amp |
I2 = ΔV 2 / R2 I2 = (60 V) / (12 Ω) I2 = 5.00 amp |
I3 = ΔV 3 / R3 I3 = (60 V) / (11 Ω) I3 = 5.45 amp |
As a check of the accuracy of the mathematics performed, it
is wise to see if the calculated values satisfy the principle that the sum of
the current values for each individual resistor is equal to the total current
in the circuit (or in the battery). In other words, is Itot = I1 + I2 + I3 ?
Is Itot =
I1 + I2 + I3 ?
Is 14.0 amp = 3.53 amp + 5.00 amp + 5.45 amp ?
Is 14.0 amp = 13.98 amp ?
Yes!!
(The 0.02 amp difference is simply the result of having
previously rounded the Itot value from 13.98.)
The mathematical analysis of this parallel
circuit involved a blend of concepts and equations. As is often the case in
physics, the divorcing of concepts from equations when embarking on the
solution to a physics problem is a dangerous act. Here, one must consider the
concepts that the voltage drops across each one of the three resistors is equal
to the battery voltage and that the sum of the current in each resistor is
equal to the total current. These understandings are essential in order to
complete the mathematical analysis. In the next part of Lesson 4, combination or compound circuits in which some devices are in parallel
and others are in series will be investigated.
Check Your Understanding
1. As more and more resistors are added in parallel to a
circuit, the equivalent resistance of the circuit ____________ (increases,
decreases) and the total current of the circuit ____________ (increases,
decreases).
Answers:
As more and more
resistors are added in parallel to a circuit, the equivalent resistance of the
circuit decreases and the total current
of the circuit increases.
Adding more
resistors in parallel is equivalent to providing more branches through which
charge can flow. Even though the added branches offer resistance to the flow of
charge, the overall resistance decreases due to the fact that there are additional
pathways available for charge flow. The fraction of the total charge which
encounters a single resistor is now less. The additional branches mean that the
circuit can sustain a greater current.
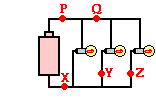2. Three identical light bulbs are connected to a D-cell as shown below.
P, Q, X, Y and Z represent locations along the circuit. Which one of the
following statements is true?
a.
The current at Y is greater than the current at Q.
b. The current at Y is greater than the current at P.
c. The current at Y is greater than the current at Z.
d. The current at P is greater than the current at Q.
e. The current at Q is greater than the current at P.
f. The current is the same at all locations.
Answer: D
Points P and X
are outside the branches; they are at locations before (P) and
after (X) the nodes. The current at these two locations are the same. The
current at these locations are greater than the current at the other three
locations since points P and X represent locations through which every charge
must flow. Point Q comes after the node and at a location where charge to the
middle and the right branch will flow. The current at this location is the
greater than the current at locations Y and Z. Locations Y and Z represent
locations where charge through a single branch will flow. The current at Y and
Z is equal, but less than that at P.
close
3. Three identical light bulbs are connected to a D-cell as shown below.
P, Q, X, Y and Z represent locations along the circuit. At which location(s),
if any, will the current be ...
a.
... the same as at X?
b. ... the same as at Q?
c. ... the same as at Y?
d. ... less than at Q?
e. ... less than at P?
f. ... twice that at Z?
g. ... three times that at Y?
Answers:
a. ... the same as at
X? P
b. ... the same as at Q? None
c. ... the same as at Y? Z
d. ... less than at Q? Y, Z
e. ... less than at P? Q, Y, Z
f. ... twice that at Z? Q
g. ... three times that at Y? P, X
Discussion: Point P represents a location outside the branches
through which charge flowing to all three branches must pass. Point X
represents a location outside the branches through which charge flowing from
all three branches must pass. Thus, the current at points P and X are equal to
each other and greater than the current in any single branch and greater than
the current in two branches combined.
Points Y and Z represent locations inside of a single branch.
Since the bulbs are identical (have the same resistance), the current in each
of the three branches is the same. Thus the current at Y and Z are equal.
Point Q represents a point through which all charge which flows
to the middle and the rightmost branch must pass. In a sense, it feeds the
branches where points Y and Z are located. As such, the current at Q is greater
than the current at Y and Z. In fact, the current at Q is twice as great as the
current at either Y or Z.
To put sample
numbers on this problem, we could say that the current at P and X is 6 Amps and
the current in each branch is 2 Amps. The current at location Y is 2 Amps and
the current at location Z is 2 Amps. The current at location Q is 4 Amps.
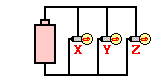4. Which adjustments could be made to the circuit below that would
decrease the current in the cell? List all that apply.
a.
Increase the resistance of bulb X.
b. Decrease the resistance of bulb X.
c. Increase the resistance of bulb Z.
d. Decrease the resistance of bulb Z.
e. Increase the voltage of the cell (somehow).
f. Decrease the voltage of the cell (somehow).
g. Remove bulb Y.
Answers: A, C, F, and G
The current in
the battery is dependent upon the electric potential difference across the
battery (
V) and the
total or equivalent resistance of the circuit (Req). A decrease in V
(choice F) and an increase in Req would
lead to a decrease in the current at the battery location. The overall
resistance can be increased by increasing the resistance of any of the light
bulbs (choices A and C) or by reducing the number
of branches (choice G)
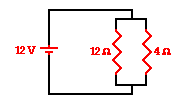5. A 12-V battery , a 12-ohm resistor
and a 4-ohm resistor are connected as shown. The current in the 12-ohm resistor
is ____ that in the 4-ohm resistor.
|
a. 1/3 |
b. 1/2 |
c. 2/3 |
|
|
d. the
same as |
e. 1.5
times |
||
|
f. twice |
g. three
times |
||
|
h. four
times |
|
|
|
Answer: A
In parallel circuits, the
electric potential difference across each resistor (ΔV) is the same. The
current in a resistor follows Ohm's law: I = ΔV / R. Since the ΔV is
the same for each resistor, the current will be smallest where the resistance
is greatest. In fact, a resistor with three times the resistance will have
one-third the current in order for the product of I•R to be the same. In this
circuit, each resistor has a ΔV of 12 Volts. The 12-ohm resistor would
have a current of 1 Amp (using Ohm's law equation) and the 4-ohm resistor would
have a current of 3 Amps (using Ohm's law equation).
6. A 12-V battery , a 12-ohm resistor
and a 4-ohm resistor are connected as shown. The voltage drop across the 12-ohm
resistor is ____ that across the 4-ohm resistor.
|
a. 1/3 |
b. 1/2 |
c. 2/3 |
|
|
d. the
same as |
e. 1.5
times |
||
|
f. twice |
g. three
times |
||
|
h. four
times |
|
|
|
Answer: D
In a parallel
circuit, the voltage drops across each of the branches is the same as the
voltage gain in the battery. Thus, the voltage drop is the same across each of
these resistors.
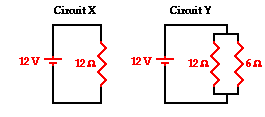7. A 12-V battery and a 12-ohm resistor are connected as shown in
circuit. A 6-ohm resistor is added to the 12-ohm resistor to create circuit Y
as shown. The voltage drop across the 6-ohm resistor in circuit Y is ____ that
across the resistor in X.
a. larger than
b. smaller than
c. the same as
Answer: C
In a parallel
circuit, the voltage drops across each of the branches is the same as the
voltage gain in the battery. Circuits X and Y are each powered by a 12-Volt
source. Thus, the voltage drop across all three resistors of the two circuits
is 12 Volts.
8. Use your understanding of equivalent resistance to
complete the following statements:
a.
Two 6-Ω resistors placed in parallel would provide a resistance that is
equivalent to one _____-Ω resistor.
b. Three 6-Ω resistors placed in parallel would provide
a resistance that is equivalent to one _____-Ω resistor.
c. Three 8-Ω resistors placed in parallel would provide
a resistance that is equivalent to one _____-Ω resistor.
d. Three resistors with resistance values of 2-Ω,
4-Ω, and 6-Ω are placed in parallel. These would provide a resistance
that is equivalent to one _____-Ω resistor.
e. Three resistors with resistance values of 5-Ω,
6-Ω, and 7-Ω are placed in parallel. These would provide a resistance
that is equivalent to one _____-Ω resistor.
f. Three resistors with resistance values of 12-Ω,
6-Ω, and 21-Ω are placed in parallel. These would provide a
resistance that is equivalent to one _____-Ω resistor.
In each case, use the equation
1/Req = 1/R1 + 1/R2 +
1/R3
to calculate the
equivalent resistance.
Answers:
a. Two 6-Ω resistors placed in parallel would provide a
resistance which is equivalent to one 3-Ω resistor.
b. Three 6-Ω resistors placed in parallel would
provide a resistance which is equivalent to one 2-Ω resistor.
c. Three 8-Ω resistors placed in parallel would
provide a resistance which is equivalent to one 2.67-Ω resistor.
d. Three resistors with resistance values of 2-Ω , 4-Ω , and 6-Ω are
placed in parallel. These would provide a resistance which is equivalent to
one 1.09-Ω resistor.
e. Three resistors with resistance values of 5-Ω , 6-Ω , and 7-Ω are
placed in parallel. These would provide a resistance which is equivalent to
one 1.96-Ω resistor.
f. Three
resistors with resistance values of 12-Ω , 6-Ω ,
and 21-Ω are placed in parallel. These would provide a resistance
which is equivalent to one 3.36-Ω resistor.
9. Based on your answers to the above question, complete the
following statement:
The overall or equivalent resistance of three resistors
placed in parallel will be _____.
a. greater than the resistance of the biggest R
value of the three.
b. less than the
resistance of the smallest R value of the three.
c. somewhere in
between the smallest R and the biggest R value of the three.
d. ... nonsense! No such generalization can be made. The
results vary.
Answer: B
An observation
of the answers to question #8 reveals that in every case, the total resistance
is less than the resistance of each individual resistance.
10. Three resistors are connected in parallel. If placed in a
circuit with a 12-volt power supply. Determine the equivalent resistance, the
total circuit current, and the voltage drop across and current in each resistor.
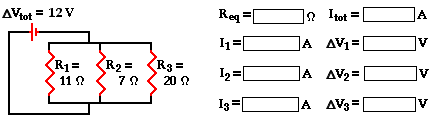
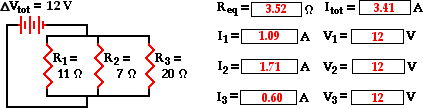
The analysis begins by using the resistance values for the
individual resistors in order to determine the equivalent resistance of the
circuit.
1 / Req = 1 / R1 + 1 / R2 +
1 / R3 = (1 / 11 Ω) + (1 / 7 Ω
) + (1 / 20 Ω)
1 / Req = 0.283766 Ω-1
Req = 1 / (0.283766 Ω-1)
Req = 3.52 Ω
(rounded from 3.524027 Ω)
Now that the equivalent resistance is known, the current in the
battery can be determined using the Ohm's law equation. In using the Ohm's law
equation (ΔV = I • R) to determine the current in the circuit, it is
important to use the battery voltage for ΔV and the equivalent resistance
for R. The calculation is shown here:
Itot = ΔVbattery / Req =
(12 V) / (3.524027 Ω)
Itot = 3.41 Amp
(rounded from 3.4051948 Amp)
The 12 V battery voltage represents the gain in electric
potential by a charge as it passes through the battery. The charge loses this
same amount of electric potential for any given pass through the external
circuit. That is, the voltage drop across each one of the three resistors is
the same as the voltage gained in the battery:
ΔV battery = ΔV 1 =
ΔV 2 = ΔV 3 = 12 V
There are three values left to be determined - the current in
each of the individual resistors. Ohm's law is used once more to determine the
current values for each resistor - it is simply the voltage drop across each
resistor (12 Volts) divided by the resistance of each resistor (given in the
problem statement). The calculations are shown below.
|
I1 = ΔV1 /
R1 I1 =
(12 V) / (11 Ω) I1 = 1.091 Amp |
I2 = ΔV 2 /
R2 I2 =
(12 V) / (7 Ω) I2 = 1.714 Amp |
I3 = ΔV 3 /
R3 I3 =
(12 V) / (20 Ω) I3 = 0.600 Amp |
As a check of the accuracy of the mathematics performed, it is
wise to see if the calculated values satisfy the principle that the sum of the
current values for each individual resistor is equal to the total current in
the circuit (or in the battery). In other words, is Itot = I1 +
I2 + I3 ?
Is Itot = I1 + I2 + I3 ?
Is 3.405 Amp = 1.091 Amp + 1.714 Amp + 0.600 Amp ?
Is 3.405 Amp = 3.405 Amp?
Yes!!