Resistance

An electron traveling through the wires and loads of the external circuit encounters resistance. Resistanceis the hindrance to the flow of charge. For an electron, the journey from terminal to terminal is not a direct route. Rather, it is a zigzag path that results from countless collisions with fixed atoms within the conducting material. The electrons encounter resistance - a hindrance to their movement. While the electric potential difference established between the two terminals encouragesthemovement of charge, it is resistance that discourages it. The rate at which charge flows from terminal to terminal is the result of the combined effect of these two quantities.

Variables Affecting Electrical Resistance

The flow of charge through wires is often compared to the flow of water through pipes. The resistance to the flow of charge in an electric circuit is analogous to the frictional effects between water and the pipe surfaces as well as the resistance offered by obstacles that are present in its path. It is this resistance that hinders the water flow and reduces both its flow rate and its drift speed. Like the resistance to water flow, the total amount of resistance to charge flow within a wire of an electric circuit is affected by some clearly identifiable variables.

First, the total length of the wires will affect the amount of resistance. The longer the wire, the more resistance that there will be. There is a direct relationship between the amount of resistance encountered by charge and the length of wire it must traverse. After all, if resistance occurs as the result of collisions between charge carriers and the atoms of the wire, then there is likely to be more collisions in a longer wire. More collisions mean more resistance.

Second, the cross-sectional area of the wires will affect the amount of resistance. Wider wires have a greater cross-sectional area. Water will flow through a wider pipe at a higher rate than it will flow through a narrow pipe. This can be attributed to the lower amount of resistance that is present in the wider pipe. In the same manner, the wider the wire, the less resistance that there will be to the flow of electric charge. When all other variables are the same, charge will flow at higher rates through wider wires with greater cross-sectional areas than through thinner wires.

A third variable that is known to affect the resistance to charge flow is the material that a wire is made of. Not all materials are created equal in terms of their conductive ability. Some materials are better conductors than others and offer less resistance to the flow of charge. Silver is one of the best conductors but is never used in wires of household circuits due to its cost. Copper and aluminum are among the least expensive materials with suitable conducting ability to permit their use in wires of household circuits. The conducting ability of a material is often indicated by its resistivity. The resistivity of a material is dependent upon the material's electronic structure and its temperature. For most (but not all) materials, resistivity increases with increasing temperature. The table below lists resistivity values for various materials at temperatures of 20 degrees Celsius.

Material	Resistivity (ohm•meter)
Silver	1.59 x 10^-8
Copper	1.7 x 10^-8
Gold	2.2 x 10^-8
Aluminum	2.8 x 10^-8
Tungsten	5.6 x 10^-8
Iron	10 x 10^-8
Platinum	11 x 10^-8
Lead	22 x 10^-8
Nichrome	150 x 10^-8
Carbon	3.5 x 10^-5
Polystyrene	10^7- 10^11
Polyethylene	10^8- 10^9
Glass	10^10- 10^14
Hard Rubber	10^13

As seen in the table, there is a broad range of resistivity values for various materials. Those materials with lower resistivities offer less resistance to the flow of charge; they are better conductors. The materials shown in the last four rows of the above table have such high resistivity that they would not even be considered to be conductors.

Mathematical Nature of Resistance

Resistance is a numerical quantity that can be measured and expressed mathematically. The standard metric unit for resistance is the ohm, represented by the Greek letter omega - . An electrical device having a resistance of 5 ohms would be represented as R = 5 . The equation representing the dependency of the resistance (R) of a cylindrically shaped conductor (e.g., a wire) upon the variables that affect it is

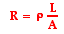
where L represents the length of the wire (in meters), A represents the cross-sectional area of the wire (in meters²), and represents the resistivity of the material (in ohm•meter). Consistent with the discussion above, this equation shows that the resistance of a wire is directly proportional to the length of the wire and inversely proportional to the cross-sectional area of the wire. As shown by the equation, knowing the length, cross-sectional area and the material that a wire is made of (and thus, its resistivity) allows one to determine the resistance of the wire.

Check Your Understanding

1. Household circuits are often wired with two different widths of wires: 12-gauge and 14-gauge. The 12-gauge wire has a diameter of 1/12 inch while the 14-gauge wire has a diameter of 1/14 inch. Thus, 12-gauge wire has a wider cross section than 14-gauge wire. A 20-Amp circuit used for wall receptacles should be wired using 12-gauge wire and a 15-Amp circuit used for lighting and fan circuits should be wired using 14-gauge wire. Explain the physics behind such an electrical code.

See Answer

A 12-gauge wire is wider than 14-gauge wire and thus has less resistance. The lesser resistance of 12-gauge wire means that it can allow charge to flow through it at a greater rate - that is, allow a larger current. Thus, 12-gauge wire is used in circuits which are protected by 20-Amp fuses and circuit breakers. On the other hand, the thinner 14-gauge wire can support less current owing to its larger resistance; it is used in circuits which are protected by 15-Amp fuses and circuit breakers.

2. Based on the information stated in the above question, explain the risk involved in using 14-gauge wire in a circuit that will be used to power an 16-ampere power saw.

See Answer

A 12-gauge wire is wider than 14-gauge wire and thus has less resistance. The lesser resistance of 12-gauge wire means that it can allow charge to flow through it at a greater rate - that is, allow a larger current. Thus, 12-gauge wire can safely support a circuit that uses an appliance drawing up to 20 Amps of current. In fact, a 20-Amp circuit is protected by a fuse or circuit breaker that will flip off when the current reaches 20 Amps. If a 14-gauge wire was used on the same circuit, then the breaker would allow up to 20 Amps to flow through it. It could overheat and thus lead to the risk of fire. A 20-Amp circuit should never be wired using 14-gauge wire.

3. Determine the resistance of a 1-mile length of 12-gauge copper wire. Given: 1 mile = 1609 meters and diameter = 0.2117 cm.

See Answer

Answer: 7.8 ohms

Use the equation

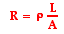
where L = 1609 m, A = PI•R² (in meters²), and  = 1.7 x 10^-8 ohm•meter. First find the cross-sectional area:

A = PI•R² = (PI) • [ (0.002117 m) / 2)]² = 3.519 x 10^-6 m²

Now substitute into the above equation to determine the resistance.

R = (1.7 x 10^-8 ohm •m) • (1609 m) / (3.519 x 10^-6 m²)

R = 7.8  (7.7709 ohm)

4. Two wires - A and B - with circular cross-sections have identical lengths and are made of the same material. Yet, wire A has four times the resistance of wire B. How many times greater is the diameter of wire B than wire A?

See Answer

Answer: D_B = 2 • D_A

If wire A has four times the resistance, then it must have the smaller cross-sectional area since resistance and cross-sectional area are inversely proportional. In fact, A must have one-fourth the cross-sectional area of B. Since the cross-sectional area of a circular cross-section is given by the expression PI•R², wire A must have one-half the radius of wire B and therefore one-half the diameter. Put another way, the diameter of wire B is two times greater than the diameter of wire A.