Calorimeters and Calorimetry
Calorimetry is the
science associated with determining the changes in energy of a system by
measuring the heat exchanged with the surroundings. Now that sounds very textbooky; but in this last part of Lesson 2, we are going to try to
make some meaning of this definition of calorimetry. In physics class (and for
some, in chemistry class), calorimetry labs are frequently performed in order
to determine the heat of reaction or the heat of fusion or the heat of
dissolution or even the specific heat capacity of a metal. These types of labs
are rather popular because the equipment is relatively inexpensive and the
measurements are usually straightforward. In such labs, a calorimeter is used.
A calorimeter is a device
used to measure the quantity of heat transferred to or from an object. Most
students likely do not remember using such afancy piece of equipment known as a
calorimeter. Fear not; the reason for the lack of memory is not a sign of early
Alzheimer's. Rather, it is because the calorimeter used in high school science
labs is more commonly referred to as a Styrofoam cup. It is a coffee cup
calorimeter - usually filled with water. The more sophisticated cases
include a lid on the cup with an inserted thermometer and maybe even a stirrer.
Coffee Cup
Calorimetry
So how can such
simple equipment be used to measure the quantity of heat gained or lost by a
system? We have learned on the previous page, that water will change its
temperature when it gains or loses energy. And in fact, the quantity of energy
gained or lost is given by the equation
Q = mwater•Cwater•ΔTwater
where Cwater is 4.18 J/g/°C. So
if the mass of water and the temperature change of the water in the coffee cup
calorimeter can be measured, the quantity of energy gained or lost by the water
can be calculated.
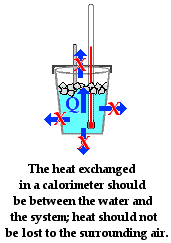The assumption behind the science of calorimetry is that the energy
gained or lost by the water is equal to the energy lost or gained by the object
under study. So if an attempt is being made to determine the specific heat of
fusion of ice using a coffee cup calorimeter, then the assumption is that the
energy gained by the ice when melting is equal to the energy lost by the
surrounding water. It is assumed that there is a heat exchange between
the iceand the water in the cup and that no other objects are involved in the
heat exchanged. This statement could be placed in equation form as
Qice = - Qsurroundings = -Qcalorimeter
The role of the
Styrofoam in a coffee cup calorimeter is that it reduces the amount of heat
exchange between the water in the coffee cup and the surrounding air. The value
of a lid on the coffee cup is that it also reduces the amount of heat exchange
between the water and the surrounding air. The more that these other heat
exchanges are reduced, the more true that the above mathematical equation will
be. Any error analysis of a calorimetry experiment must take into consideration
the flow of heat from system to calorimeter to other parts of thesurroundings. And any design of a calorimeter experiment must give attention to
reducing the exchanges of heat between the calorimeter contents and the surroundings.
Bomb Calorimetry
The coffee cup
calorimeters used in high school science labs provides students with a
worthwhile exercise in calorimetry. But at the professional level, a cheap
Styrofoam cup and a thermometer isn't going to assist a commercial food
manufacturer in determining the Calorie content of their products. For
situations in which exactness and accuracy is at stake, a more expensive
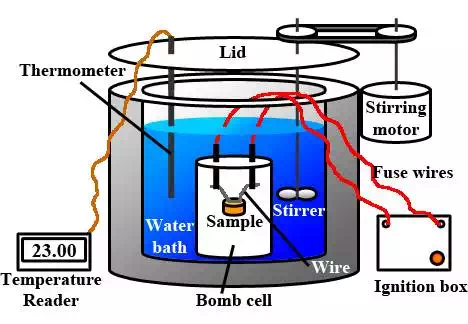
calorimeter is needed. Chemists often use a device known as a bomb calorimeter to measure the heat exchanges associated with
chemical reactions, especially combustion reactions. Having little to nothing
to do with bombs of the military variety, a bomb calorimeter includes a
reaction chamber where the reaction (usually a combustion reaction) takes
place. The reaction chamber is a strong vessel that can withstand the intense
pressure of heated gases with exploding. The chamber is typically filled with
mostly oxygen gas and the fuel. An electrical
circuit is wired into the chamber in order to electrically ignite the contents
in order to perform a study of the heat released upon combustion. The reaction
chamber is surrounded by a jacket of water with a thermometer inserted. The
heat released from the chamber warms the water-filled jacket, allowing a
scientist to determine the quantity of energy released by the reaction.
Solving
Calorimetry Problems
Now let's look at a
few examples of how a coffee cup calorimeter can be used as a tool to answer
some typical lab questions. The next three examples are all based on laboratory
experiments involving calorimetry.
Example Problem 1:
A physics class has been assigned the task of determining an experimental value
for the heat of fusion of ice. Anna Litical and Noah Formula dry and mass out 25.8-gram
of ice and place it into a coffee cup with 100.0 g of water at 35.4°C. They
place a lid on the coffee cup and insert a thermometer. After several minutes,
the ice has completely melted and the water temperature has lowered to 18.1°C.
What is their experimental value for the specific heat of fusion of ice?
The basis for the
solution to this problem is the recognition that the quantity of energy lost by
the water when cooling is equal to the quantity of energy required to melt the
ice. In equation form, this could be stated as
Qice = -Qcalorimeter
(The negative sign
indicates that the ice is gaining energy and the water in the calorimeter is
losing energy.) Here the calorimeter (as in the Qcalorimeter term) is
considered to be the water in the coffee cup. Since the mass of this water and
its temperature change are known, the value of Qcalorimeter can be determined.
Qcalorimeter = m•C•ΔT
Qcalorimeter = (100.0 g)•(4.18 J/g/°C)•(18.1°C - 35.4°C)
Qcalorimeter = -7231.4 J
The negative sign indicates that the water lost energy. The assumption
is that this energy lost by the water is equal to the quantity of energy gained
by the ice. So Qice = +7231.4 J. (The
positive sign indicates an energy gain.) This value can be used with the
equation from the previous page to determine the heat of fusion of the ice.
Qice = mice•ΔHfusion-ice
+7231.4 J = (25.8 g)•ΔHfusion-ice
ΔHfusion-ice = (+7231.4 J)/(25.8 g)
ΔHfusion-ice = 280.28 J/g
ΔHfusion-ice = 2.80x102 J/g (rounded to two
significant figures)
Example Problem 2:
A chemistry student dissolves 4.51 grams of sodium hydroxide in 100.0 mL of
water at 19.5°C (in a calorimeter cup). As the sodium hydroxide dissolves, the
temperature of the surrounding water increases to 31.7°C. Determine the heat of
solution of the sodium hydroxide in J/g.
Once more, the
solution to this problem is based on the recognition that the quantity of
energy released when sodium hydroxide dissolves is equal to the quantity of
energy absorbed by the water in the calorimeter. In equation form, this could
be stated as
QNaOH dissolving = -Qcalorimeter
(The negative sign
indicates that the NaOH is losing energy and the water in the calorimeter is gaining
energy.) Since the mass and temperature change of the water have been measured,
the energy gained by the water (calorimeter) can be determined.
Qcalorimeter = m•C•ΔT
Qcalorimeter = (100.0 g)•(4.18 J/g/°C)•(31.7°C - 19.5°C)
Qcalorimeter = 5099.6 J
The assumption is
that this energy gained by the water is equal to the quantity of energy
released by the sodium hydroxide when dissolving. So QNaOH-dissolving = -5099.6 J. (The negative sign indicates an
energy lost.) This quantity is the amount of heat released when dissolving 4.51
grams of the sodium hydroxide. When the heat of solution is determined on a per
gram basis, this 5099.6 J of energy must be divided by the mass of sodium
hydroxide that is being dissolved.
ΔHsolution = QNaOH-dissolving / mNaOH
ΔHsolution = (-5099.6 J) /
(4.51 g)
ΔHsolution = -1130.7 J/g
ΔHsolution = -1.13x103 J/g (rounded to three significant figures)
Example Problem 3:
A large paraffin candle has a mass of 96.83 gram. A metal cup with 100.0 mL of
water at 16.2°C absorbs the heat from the burning candle and increases its
temperature to 35.7°C. Once the burning is ceased, the temperature of the water
was 35.7°C and the paraffin had a mass of 96.14 gram. Determine the heat of
combustion of paraffin in kJ/gram. GIVEN: density of water = 1.0 g/mL.
As is always the
case, calorimetry is based on the assumption that all the heat lost by the system is gained by the surroundings. It is assumed that the surroundings is the water that
undergoes the temperature change. In equation form, it could be stated that
Qparaffin = -Qwater
Since the mass and
temperature change of the water are known, the energy gained by the water in
the calorimeter can be determined.
Qcalorimeter = m•C•ΔT
Qcalorimeter = (100.0 g)•(4.18 J/g/°C)•(35.7°C - 16.2°C)
Qcalorimeter = 8151 J
The paraffin
released 8151 J or 8.151 kJ of energy when burned. This is based on the burning
of 0.69 gram (96.83 g - 96.14 g). To determine the heat of combustion on a per
gram basis, the Qparaffin value (-8.151 kJ)
must be divided by the mass of paraffin burned:
ΔHcombustion - paraffin = (-8.151 kJ) /
(0.69 g)
ΔHcombustion - paraffin = -11.813 kJ/g
ΔHcombustion - paraffin = -12 kJ/g (rounded to two significant digits)
Check Your Understanding
1. Consider Example
Problem 3 above. Identify as many sources of error as you can. For each source
indicate the direction of error that would have resulted. That is, identify
whether the error would have caused the experimentally derived value to be less
than or more than the accepted value.
Answer:
Answers will vary.
Three common choices include:
A. Energy is
transferred from the water to the surrounding air. This would cause the
experimental value to be less than the accepted value since this energy is not
contributing to the water's temperature change.
B. Energy is being
absorbed by the metal cup as the metal also encounters a temperature change.
This would cause since this energy is not being accounted for in the
calculations.
C. Some of the
energy released by the burning candle fails to warm either the cup or the
water. This energy simply warms the surrounding air. Failure to account for
this energy would cause the experimental value to be less than the accepted
value.
2. A 2.15-gram
cashew nut is burned. The heat released raises the temperature of a 100.0-gram
sample of water from 18.2°C to 31.5°C. The mass of the nut after the experiment
is 1.78 grams. Determine the calorie content of the nut in Calories/gram.
Assume that the water is only able to absorb 25% of the heat released by the
burning nut. Given 1.00 Calorie=4.18 kJ.
Answer: ~15
Cal/g
Qwater = mwater•Cwater•ΔTwater
Qwater = (100.0 g)•(4.18J/g/°C)•(31.5°C - 18.2°C) = 5559.4 J = 5.5594 kJ
Qwater = 5.5594 kJ•(1.00 Calorie/4.18 kJ) = 1.3560 Calorie
The energy
absorbed by the water is one-fourth (25%) of the energy released by the nut.
Qnut = -1.3560 Calorie/0.25
= -5.4238 Calorie
This 5.4238
Calorie of energy was released by burning 0.37 grams of the Cashew. To
determine the Calorie content on a per gram basis, the Calorie-to-gram ratio must
be determined.
Calorie Content =
5.4248 Calorie/0.37 gram = 14.6589 Cal/g
Calorie content
= 15 Calorie/gram (rounded to two significant figures)