Rates of Heat Transfer
On previous pages of this lesson, we have learned that heat is a
form of energy transfer from a high temperature location to a low
temperature location. The three main methods of heat transfer - conduction,
convection and radiation - were discussed in detail on the previous
page. Now we will investigate the topic of the rate
of heat transfer. This topic is of great importance because of the frequent
need to either increase or decrease the rate at which heat flows between two
locations. For instance, those of us who live in colder winter climates are in
constant pursuit of methods of keeping our homes warm without spending too much
money. Heat escapes from higher temperature homes to the lower temperature
outdoors through walls, ceilings, windows and doors. We make efforts to reduce
this heat loss by adding better insulation to walls and attics, caulking
windows and doors, and buying high efficiency windows and doors. As another
example, consider electricity generation. Household electricity is most
frequently manufactured by using fossil fuels or nuclear fuels. The method involves generating heat in a reactor. The heat is
transferred to water and the water carries the heat to a steam turbine (or
other type of electrical generator) where the electricity
is produced. The challenge is to efficiently transfer the
heat to the water and to the steam turbine with as little loss as possible.
Attention must be given to increasing heat transfer rates in the reactor and in
the turbine and decreasing heat transfer rates in the pipes between the reactor
and the turbine.
So what variables would affect the heat transfer rates? How
can the rate of heat transfer be controlled? These are the questions to be
discussed on this page of Lesson 1. Our discussion will be restricted to the
variables affecting the rate of heat transfer by conduction. Once the variables affecting the rate of heat transfer are discussed,
we will look at a mathematical equation that expresses the dependence of rate
upon these variables.
Temperature Difference
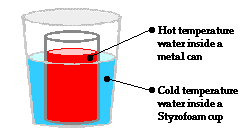In conduction, heat is transferred from a hot temperature location to a
cold temperature location. The transfer of heat will continue as long as there
is a difference in temperature between the two locations. Once the two locations
have reached the same temperature, thermal equilibrium is established and the
heat transfer stops. Earlier in this lesson, we discussed the transfer of heat for a situation involving a metal
can containing high temperature water that was placed within a Styrofoam cup
containing low temperature water. If the two water samples are equipped with
temperature probes that record changes in temperature with respect to time,
then the following graphs are produced.
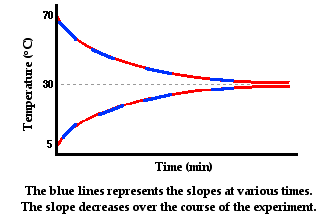
In the graphs above, the slope of the line represents the
rate at which the temperature of each individual sample of water is changing.
The temperature is changing because of the heat transfer from the hot to the
cold water. The hot water is losing energy, so its slope is negative. The cold
water is gaining energy, so its slope is positive. The rate at which
temperature changes is proportional to the rate at which heat is transferred.
The temperature of a sample changes more rapidly if heat is transferred at a
high rate and less rapidly if heat is transferred at a low rate. When the two
samples reach thermal equilibrium, there is no more heat transfer and the slope
is zero. So we can think of the slopes as being a measure of the rate of heat
transfer. Over the course of time, the rate of heat transfer is decreasing.
Initially heat is being transferred at a high rate as reflected by the steeper
slopes. And as time progresses, the slopes of the lines are becoming less steep
and more gently sloped.
What variable contributes to this decrease in the heat
transfer rate over the course of time? Answer: the difference in temperature
between the two containers of water. Initially, when the rate of heat transfer
is high, the hot water has a temperature of 70°C and the cold water has a
temperature of 5°C. The two containers have a 65°C difference in temperature.
As the hot water begins to cool and the cold water begins to warm, the
difference in their temperatures decrease and the rate of heat transfer
decreases. As thermal equilibrium is approached, their temperatures are
approaching the same value. With the temperature difference approaching zero,
the rate of heat transfer approaches zero. In conclusion, the rate of
conductive heat transfer between two locations is affected by the temperature
difference between the two locations.
Material
The first variable that we have identified as affecting the
rate of conductive heat transfer is the temperature difference between the two
locations. The second variable of importance is the materials involved in the
transfer. In the previous discussed scenario, a metal can containing high
temperature water was placed within a Styrofoam cup containing low temperature
water. The heat was transferred from water through the metal to water. The
materials of importance were water, metal and water. What would happen if the
heat were transferred from hot water through glass to cold water? What would
happen if the heat were transferred from hot water through Styrofoam to cold
water? Answer: the rate of heat transfer would be different. Replacing the
inner metal can with a glass jar or a Styrofoam cup would change the rate of
heat transfer. The rate of heat transfer depends on the material through which
heat is transferred.
The effect of a material upon heat transfer rates is often
expressed in terms of a number known as thethermal conductivity. Thermal conductivity values are numerical values that are determined
by experiment. The higher that the value is for a particular material, the more
rapidly that heat will be transferred through that material. Materials with
relatively high thermal conductivities are referred to asthermal conductors. Materials with relatively low thermal conductivity values are referred
to as thermal insulators. The table below lists thermal conductivity values (k) for a variety of
materials, in units of W/m/°C.
|
Material |
|
k |
|
Material |
k |
|
Aluminum (s) |
|
237 |
|
Sand (s) |
0.06 |
|
Brass (s) |
|
110 |
|
Cellulose (s) |
0.039 |
|
Copper (s) |
|
398 |
|
Glass wool (s) |
0.040 |
|
Gold (s) |
|
315 |
|
Cotton wool (s) |
0.029 |
|
Cast Iron (s) |
|
55 |
|
Sheep's wool (s) |
0.038 |
|
Lead (s) |
|
35.2 |
|
Cellulose (s) |
0.039 |
|
Silver (s) |
|
427 |
|
Expanded Polystyrene (s) |
0.03 |
|
Zinc (s) |
|
113 |
|
Wood (s) |
0.13 |
|
Polyethylene (HDPE) (s) |
|
0.5 |
|
Acetone (l) |
0.16 |
|
Polyvinyl chloride (PVC) (s) |
|
0.19 |
|
Water (l) |
0.58 |
|
Dense Brick (s) |
|
1.6 |
|
Air (g) |
0.024 |
|
Concrete (Low Density) (s) |
|
0.2 |
|
Argon (g) |
0.016 |
|
Concrete (High Density) (s) |
|
1.5 |
|
Helium (g) |
0.142 |
|
Ice (s) |
|
2.18 |
|
Oxygen (g) |
0.024 |
|
Porcelain (s) |
|
1.05 |
|
Nitrogen (g) |
0.024 |
Source: http://www.roymech.co.uk/Related/Thermos/Thermos_HeatTransfer.html
As is apparent from the table, heat is generally transferred
by conduction at considerably higher rates through solids (s) in comparison to
liquids (l) and gases (g). Heat transfer occurs at the highest rates for metals
(first eight items in left-hand column) because the mechanism of conduction
includes mobile electrons (as discussed on a previous
page). Several of the solids in the right-hand
column have very low thermal conductivity values and are considered insulators.
The structure of these solids is characterized by pockets of trapped air
interspersed between fibers of the solid.
Since air is a great insulator, the pockets of air interspersed between these
solid fibers gives these solids low thermal
conductivity values. One of these solid insulators is expanded polystyrene, the
material used in Styrofoam products. Such Styrofoam products are made by
blowing an inert gas at high pressure into the polystyrene before being
injected into the mold. The gas causes the
polystyrene to expand, leaving air filled pockets that contribute to the insulating
ability of the finished product. Styrofoam is used in coolers, pop can
insulators, thermos jugs, and even foam boards for household insulation.
Another solid insulator is cellulose. Cellulose insulation is used to insulate
attics and walls in homes. It insulates homes from heat loss as well as sound
penetration. It is often blown into attics as loose fill
cellulose insulation. It is also applied as fiberglass
batts (long sheets of paper backed insulation) to fill the spacing between 2x4
studs of the exterior (and sometimes interior) walls of homes.
Area
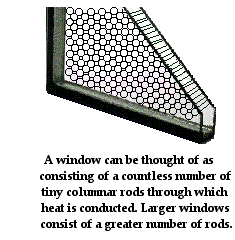Another variable that affects the rate of conductive heat transfer is
the area through which heat is being transferred. For instance, heat transfer
through windows of homes is dependent upon the size of the window. More heat
will be lost from a home through a larger window than through a smaller window
of the same composition and thickness. More heat will be lost from a home
through a larger roof than through a smaller roof with the same insulation
characteristics. Each individual particle on the surface of an object is
involved in the heat conduction process. An object with a wider area has more
surface particles working to conduct heat. As such, the rate of heat transfer
is directly proportional to the surface area through which the heat is being
conducted.
Thickness or Distance
A final variable that affects the rate of conductive heat
transfer is the distance that the heat must be conducted. Heat escaping through
a Styrofoam cup will escape more rapidly through a thin-walled cup than through
a thick-walled cup. The rate of heat transfer is inversely proportional to the
thickness of the cup. A similar statement can be made for heat being conducted
through a layer of cellulose insulation in the wall of a home. The thicker that
the insulation is, the lower the rate of heat transfer. Those of us who live in
colder winter climates know this principle quite well. We are told to dress in
layers before going outside. This increases the thickness of the materials
through which heat is transferred, as well as trapping pockets of air (with
high insulation ability) between the individual layers.
A Mathematical Equation
So far we have learned of four variables that affect the rate
of heat transfer between two locations. The variables are the temperature
difference between the two locations, the material present between the two
locations, the area through which the heat will be transferred, and the
distance it must be transferred. As is often the case in physics, the
mathematical relationship between these variables and the rate of heat transfer
can be expressed in the form of an equation. Let's consider the transfer of heat
through a glass window from the inside of a home with a temperature of T1 to the outside of a home with a temperature ofT2. The window has a surface area A and a
thickness d. The thermal
conductivity value of the window glass is k. The equation relating the heat transfer rate
to these variables is
Rate = k•A•(T1 - T2)/d
The units on the rate of heat transfer are Joule/second, also
known as a Watt. This equation is applicable to any situation in which heat is
transferred in the same direction across a flat rectangular wall. It applies to conduction through windows, flat walls, slopes roofs
(without any curvature), etc. A slightly different equation applies to
conduction through curved walls such as the walls of cans,
cups, glasses and pipes. We will not discuss that equation here.
Example Problem
To
illustrate the use of the above equation, let's calculate the rate of heat
transfer on a cold day through a rectangular window that is 1.2 m wide and 1.8
m high, has a thickness of 6.2 mm, a thermal conductivity value of 0.27
W/m/°C. The temperature inside the home is 21°C and the temperature outside the
home is -4°C.
To solve this problem, we will need to know the surface area
of the window. Being a rectangle, we can calculate the area as width • height.
Area = (1.2 m)•(1.8 m) = 2.16 m2.
We will also need to give attention to the unit on thickness
(d). It is given in units of cm; we will need to convert to units of meters in
order for the units to be consistent with that of k and A.
d = 6.2 mm = 0.0062 m
Now we are ready to calculate the rate of heat transfer by
substitution of known values into the above equation.
Rate = (0.27 W/m/°C)•(2.16 m2)•(21°C
- -4°C)/(0.0062 m)
Rate = 2400 W (rounded
from 2352 W)
It is useful to note that the thermal conductivity value of a
house window is much lower than the thermal conductivity value of glass itself.
The thermal conductivity of glass is about 0.96 W/m/°C. Glass windows are
constructed as double and triple pane windows with a low pressure inert gas
layer between the panes. Furthermore, coatings are placed on the windows to
improve efficiency. The result is that there are a series of substances through
which heat must consecutively pass in order to be transferred out of (or into)
the house. Like electrical resistors placed in series, a series of
thermal insulators has an additive effect on the overall resistance offered to
the flow of heat. The accumulative effect of the various layers of materials in
a window leads to an overall conductivity that is much less than a single pane
of uncoated glass.
Lesson 1 of this Thermal Physics chapter has focused on the
meaning of temperature and heat. Emphasis has been given to the development of
a particle model of materials that is capable of explaining the macroscopic
observations. Efforts have been made to develop solid conceptual understandings
of the topic in the absence of mathematical formulas. This solid conceptual
understanding will serve you well as you approach. The chapter will turn
slightly more mathematical as we investigate the question: how can the amount
of heat released from or gained by a system be measured? will pertain to the science of calorimetry.
Check Your Understanding
1. Predict the effect of the following variations upon the
rate at which heat is transferred through a rectangular object by filling in
the blanks.
a. If the area through which heat is transferred is increased
by a factor of 2, then the rate of heat transfer is ________________
(increased, decreased) by a factor of _________ (number).
b. If the thickness of the material through which heat is
transferred is increased by a factor of 2, then the rate of heat transfer is
________________ by a factor of _________.
c. If the thickness of the material through which heat is
transferred is decreased by a factor of 3, then the rate of heat transfer is
________________ by a factor of _________.
d. If the thermal conductivity of the material through which
heat is transferred is increased by a factor of 5, then the rate of heat
transfer is ________________ by a factor of _________.
e. If the thermal conductivity of the material through which
heat is transferred is decreased by a factor of 10, then the rate of heat
transfer is ________________ by a factor of _________.
f. If the temperature difference on opposite sides of the
material through which heat is transferred is increased by a factor of 2, then
the rate of heat transfer is ________________ by a factor of _________.
Answers:
a. If the area through which heat is transferred is increased by
a factor of 2, then the rate of heat transfer is increased by a factor of2.
b. If the thickness of the material through which heat is
transferred is increased by a factor of 2, then the rate of heat transfer isdecreased by a factor of 2.
c. If the thickness of the material through which heat is
transferred is decreased by a factor of 3, then the rate of heat transfer isincreased by a factor of 3.
d. If the thermal conductivity of the material through which
heat is transferred is increased by a factor of 5, then the rate of heat
transfer is increased by a factor of 5.
e. If the thermal conductivity of the material through which
heat is transferred is decreased by a factor of 10, then the rate of heat
transfer is decreased by a factor of 10.
f. If the
temperature difference on opposite sides of the material through which heat is
transferred is increased by a factor of 2, then the rate of heat transfer
is increased by a factor of 2.
2. Use the information on this page to explain why the 2-4
inch thick layer of blubber on a polar
bear helps to keep polar bears warm during frigid artic weather.
Answer:
The blubber has
insulating qualities, preventing the escape of heat from the interiors of the
polar bear. The thicker the blubber, the lower the rate of heat transfer.
3. Consider the example problem above. Suppose that the area
where the window is located is replaced by a wall with thick insulation. The
thermal conductivity of the same area will be decreased to 0.0039 W/m/°C and
the thickness will be increased to 16 cm. Determine the rate of heat transfer
through this area of 2.16 m2.
Answer: 1.3 W
Solution:
Rate = (0.0039 W/m/°C)•(2.16 m2)•(21°C - -4°C)/(0.16 m)
Rate = 1.3 W (rounded from 1.2352
W)