What is Heat?
Earlier in this lesson, five dictionary
style definitions of temperature were given. They were:
· The degree
of hotness or coldness of a body or environment.
· A measure
of the warmth or coldness of an object or substance with reference to some
standard value.
· A measure
of the average kinetic energy of the particles in a sample of matter, expressed
in terms of units or degrees designated on a standard scale.
· A measure
of the ability of a substance, or more generally of any physical system, to transfer
heat energy to another physical system.
· Any of
various standardized numerical measures of this ability, such as the Kelvin,
Fahrenheit, and Celsius scale
As mentioned, the first two bullet points
have rather obvious meanings. The third bullet point was the topic of the previous
page in this lesson. The fifth bullet point was the definition that
we started with as we discussed temperature and the operation of thermometers;
it was the topic of the second page in this lesson. That leaves us with the fourth bullet point - defining temperature in
terms of the ability of a substance to transfer heat to another substance. This
part of Lesson 1 is devoted to understanding how the relative temperature of
two objects affects the direction that heat is transferred between the two objects.
What
is Heat?
Consider a very hot mug of coffee on the countertop of your
kitchen. For discussion purposes, we will say that the cup of coffee has a
temperature of 80°C and that the surroundings (countertop, air in the kitchen,
etc.) has a temperature of 26°C. What do you suppose will happen in this
situation? I suspect that you know that the cup of coffee will gradually cool
down over time. At 80°C, you wouldn't dare drink the coffee. Even the
coffee mug will likely be too hot to touch. But over time, both the coffee mug
and the coffee will cool down. Soon it will be at a drinkable temperature. And
if you resist the temptation to drink the coffee, it will eventually reach room
temperature. The coffee cools from 80°C to about 26°C. So what is happening
over the course of time to cause the coffee to cool down? The answer to this
question can be both macroscopic and particulate in nature.
On the macroscopic level, we would say that the coffee and the mug are
transferring heat to the surroundings. This transfer of heat occurs from the
hot coffee and hot mug to the surrounding air. The fact that the coffee lowers
its temperature is a sign that the average kinetic energy of its particles is
decreasing. The coffee is losing energy. The mug is also lowering its
temperature; the average kinetic energy of its particles is also decreasing.
The mug is also losing energy. The energy that is lost by the coffee and the
mug is being transferred to the colder surroundings. We refer to this transfer
of energy from the coffee and the mug to the surrounding air and countertop as
heat. In this sense, heat is simply
the transfer of energy from a hot object to a colder object.
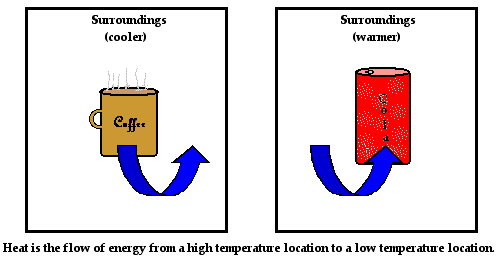
Now let's consider a different scenario - that of a cold
can of pop placed on the same kitchen
counter. For discussion purposes, we will say that the pop and the can which
contains it has a temperature of 5°C and that the surroundings (countertop, air
in the kitchen, etc.) has a temperature of 26°C. What will happen to the cold
can of pop over the course of time? Once more, I suspect that you know the
answer. The cold pop and the container will both warm up to room temperature.
But what is happening to cause these colder-than-room-temperature objects to
increase their temperature? Is the cold escaping from the pop and its container?
No! There is no such thing as the cold escaping or leaking. Rather, our explanation is very similar to the explanation used to
explain why the coffee cools down. There is a heat transfer.
Over time, the pop and the container increase their temperature. The
temperature rises from 5°C to nearly 26°C. This increase in temperature is a
sign that the average kinetic energy of the particles within the pop and the
container is increasing. In order for the particles within the pop and the
container to increase their kinetic energy, they must be gaining energy from
somewhere. But from where? Energy is being transferred from the surroundings
(countertop, air in the kitchen, etc.) in the form of heat. Just as in the case
of the cooling coffee mug, energy is being transferred from the higher
temperature objects to the lower temperature object. Once more, this is known
as heat - the transfer of energy from the higher temperature object to a lower
temperature object.
Another
Definition of Temperature
Both of these scenarios could be summarized by two simple
statements. An object decreases its temperature by releasing energy in the form
of heat to its surroundings. And an object increases its temperature by gaining
energy in the form of heat from its surroundings. Both the warming up and the cooling
down of objects works in the same way - by heat transfer from the higher
temperature object to the lower temperature object. So now we can meaningfully
re-state the definition of temperature. Temperature is a measure of the ability of a substance, or
more generally of any physical system, to transfer heat energy to another
physical system. The higher the temperature of an object is, the greater the
tendency of that object to transfer heat. The lower the temperature of an
object is, the greater the tendency of that object to be on the receiving end
of the heat transfer.
But perhaps you have been asking: what happens to the
temperature of surroundings? Do the countertop and the air in the kitchen
increase their temperature when the mug and the coffee cool down? And do the
countertop and the air in the kitchen decrease its temperature when the can and
its pop warm up? The answer is a resounding Yes!
The proof? Just touch the countertop - it should feel cooler or warmer than
before the coffee mug or pop can were placed on the countertop. But what about
the air in the kitchen? Now that's a little more difficult to present a
convincing proof of. The fact that the volume of air in the room is so large
and that the energy quickly diffuses away from the surface of the mug means
that the temperature change of the air in the kitchen will be abnormally small.
In fact, it will be negligibly small. There would have to be a lot more heat transfer before there is a
noticeable temperature change.
Thermal Equilibrium
In the discussion of the cooling of the coffee mug, the
countertop and the air in the kitchen were referred to as the surroundings. It is common in physics discussions of this type to use a mental
framework of asystem and the surroundings. The coffee mug (and the coffee) would be regarded as the system and
everything else in the universe would be regarded as the surroundings. To keep it simple, we often narrow the scope of the surroundings from
the rest of the universe to simply those objects that are immediately
surrounding the system. This approach of analyzing a
situation in terms of system and surroundings is so useful that we will adopt
the approach for the rest of this chapter and the next.
Now let's imagine a third situation. Suppose that a small
metal cup of hot water is placed inside of a larger Styrofoam cup of cold
water. Let's suppose that the temperature of the hot water is initially 70°C
and that the temperature of the cold water in the outer cup is initially 5°C.
And let's suppose that both cups are equipped with thermometers (or temperature
probes) that measure the temperature of the water in each cup over the course
of time. What do you suppose will happen? Before you read on, think about the
question and commit to some form of answer. When the cold water is done warming
and the hot water is done cooling, will their temperatures be the same or
different? Will the cold water warm up to a lower temperature than the
temperature that the hot water cools down to? Or as the warming and cooling
occurs, will their temperatures cross each other?
Fortunately, this is an experiment that can be done and in
fact has been done on many occasions. The graph below is a typical
representation of the results.
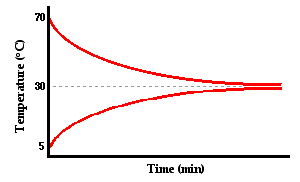
As you can see from the graph, the hot water cooled down to
approximately 30°C and the cold water warmed up to approximately the same
temperature. Heat is transferred from the high temperature object (inner can of
hot water) to the low temperature object (outer can of cold water). If we
designate the inner cup of hot water as the system, then we can say that there is a flow of heat from the system to thesurroundings. As long as there is a temperature
difference between the system and the surroundings, there is a heat flow
between them. The heat flow is more rapid at first as depicted by the steeper
slopes of the lines. Over time, the temperature difference between system and
surroundings decreases and the rate of heat transfer decreases. This is denoted
by the gentler slope of the two lines. (Detailed information about rates of
heat transfer will be discussed later in this lesson.) Eventually, the system and the surroundings reach the same
temperature and the heat transfer ceases. It is at this point, that the two
objects are said to have reached thermal equilibrium.
The Zeroeth Law of Thermodynamics
In our chapter on electric circuits, we learned that a difference in electric potential between two
locations causes a flow of charge along a conducting path between those
locations. As long as an electric potential difference is
maintained, a flow of charge will exist. Now in this chapter we learn a similar
principle related to the flow of heat. A temperature difference between two
locations will cause a flow of heat along a (thermally) conducting path between
those two locations. As long as the temperature difference is maintained, a
flow of heat will occur. This flow of heat continues until the two objects
reach the same temperature. Once their temperatures become equal, they are said
to be at thermal equilibrium and the flow of heat no longer takes place.
This principle is sometimes referred to
as the zeroeth law of
thermodynamics. This principle became formalized into a law
after the first, second and third laws of thermodynamics had already beendiscovered. But because the law seemed more
fundamental than the previously discovered three, it was titled the zeroeth law. All objects are governed by this law - this
tendency towards thermal equilibrium. It represents a daily challenge for those
who wish to control the temperature of their bodies, their food, their drinks
and their homes. We use ice and insulation to try to keep our cold drinks cold
and we use insulation and ongoing pulses of microwave energy to keep our hot
drinks hot. We equip our vehicles, our homes and our office buildings equipped
with air conditioners and fans in order to keep them cool during the warm
summer months. And we equip these same vehicles and buildings with furnaces and
heaters in order to keep them warm during the cold winter months. Whenever any
of these systems are at a different temperature as the surroundings and not
perfectly insulated from the surroundings (an ideal situation), heat will flow.
This heat flow will continue until the system and surroundings have achieved
equal temperatures. Because these systems have a considerably smaller volume
than the surroundings, there will be a more noticeable and substantial change
in temperature of these systems.
The Caloric Theory
Scientists have long pondered the nature of heat. Well into
the mid-19th century, the most accepted notion of heat was one that associated
it with a fluid known as caloric. Noted chemist Antoine Lavoisier reasoned that there were two forms of
caloric - the kind that was latent or stored
in combustible materials and the kind that was sensible and observable through a temperature change.
For Lavoisier and his followers, the burning of fuel resulted in the release of
this latent heat to the surroundings where it was observed to cause a
temperature change of the surroundings. To Lavoisier and his followers, the
heat was always present - either in latent form or in sensible form. If a hot
kettle of water cooled down to room temperature, it was explained by the flow
of caloric from the hot water to the surroundings.
According to caloric theory, heat was material in nature.
It was a physical substance. It was stuff. Like all stuff in
Lavoisier's world, caloric was a conserved substance. Similar to our modern
view of heat, the calorist view was that if
caloric was released by one object, then it was gained by another object. The
total amount of caloric never changed; it was simply transferred from one
object to another and transformed from one type (latent) to another type
(sensible). But unlike our modern view of heat, caloric was an actual physical
substance - a fluid that could flow from one object to another. And unlike our
modern view, heat was always present in one form or another. Finally, in the
modern view, heat is present only when there is an energy transfer. It is
senseless to speak of the heat as still existing once the two objects have come
to thermal equilibrium. Heat is not something contained in an object; rather it
is something transferred between objects. The heat no longer exists when the
transfer ceases.
The Fall of Caloric Theory
While there were always alternatives to the caloric theory,
it was the most accepted view up until the mid 19th century.
One of the first challenges to the caloric theory was from Anglo-American
scientist Benjamin Thompson (a.k.a., Count Rumford). Thompson was one of the
primary scientists appointed to the task of boring out the barrels of cannons
for the British government. Thompson was amazed by the high temperatures
reached by the cannons and by the shavings that were shed from the cannons
during the boring process. In one experiment, he immersed the cannon in a tank
of water during the boring process and observed that the heat generated by the
boring process was capable of boiling the surrounding water within a few hours.
Thompson demonstrated that this heat generation occurred in the absence of any
chemical or physical change in the cannon's composition. He attributed the
generation of heat to friction between the cannon and the boring tool and
argued that it could not have been the result of the flow of fluid into the
water. Thompson published a paper in 1798 that challenged the view that heat
was a fluid that was conserved. He advocated a mechanical
view of heat, suggesting that its origin was related to the motion of atoms
and not the transfer of a fluid.
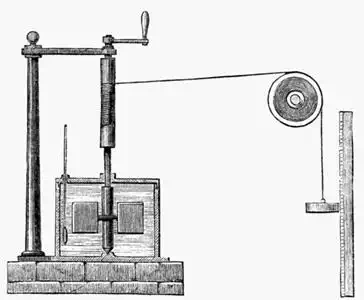English physicist James Prescott Joule took up where Thompson left off,
delivering several fateful blows to the caloric theory through a collection of
experiments. Joule, for whom the standard metric unit of energy is now named,
performed experiments in which he experimentally related the amount of
mechanical work to the amount of heat transferred from the mechanical system.
In one experiment, Joule allowed falling weights to turn a paddle wheel that
was submerged in a reservoir of water. A drawing of the apparatus is depicted
at the right (from Wikimedia; public domain). The falling
weights did work on the paddle wheel, which in turn heated the water. Joule
measured both the amount of mechanical work done and the amount of heat gained
by the water. Similar experiments demonstrating that heat could be generated by
an electric current dealt a further blow to the thought that heat was a fluid
that was contained within substances and was always conserved.
As we will learn in great detail in the next
chapter, objects possess internal energy. In chemical reactions, a portion of
this energy can be released to the surroundings in the form of heat. However,
this internal energy is not a material substance or a fluid contained by the
object. It is simply the potential energy stored in the bonds that hold
particles within the object together. Heat or thermal energy is the form this
energy possesses when it is being transferred between systems and surroundings. There is nothing material about heat. It is neither a substance nor a
fluid that is conserved. Heat is a form of energy that can be transferred from
one object to another or even created at the expense of the loss of other forms
of energy.
To review, temperature is a measure of the
ability of a substance, or more generally of any physical system, to transfer
heat energy to another physical system. If two objects - or if a system and its
surroundings - have a different temperature, then they have a different ability
to transfer heat. Over time, there will be a flow of energy from the hotter
object to the cooler object. This flow of energy is referred to as heat. The
heat flow causes the hotter object to cool down and the colder object to warm
up. The flow of heat will continue until they reach the same temperature. At
this point, the two objects have established a thermal equilibrium with each
other.
In the next part of this lesson, we will explore the mechanism of heat transfer. We will look at the
various methods by which heat can be transferred from object to object or even
from one location within an object to another. We will learn that the
macroscopic can be explained in terms of the microscopic.
Check Your Understanding
1. For each of the following designations of a system and a
surroundings, identify the direction of heat flow as being from the system to
the surroundings or from the surroundings to the system.
|
|
System |
Surroundings |
Dir'n of
Heat Transfer |
|
a. |
Living Room (T=78°F) |
Outside Air |
|
|
b. |
Living Room |
Attic |
|
|
c. |
Attic |
Outside Air |
|
Answer:
Heat is the
transfer of energy from a relatively hot location to a colder location.
|
|
System |
Surroundings |
Dir'n of Heat Transfer |
|
a. |
Living Room (T=78°F) |
Outside Air |
From surroundings to system |
|
b. |
Living Room |
Attic |
From surroundings to system |
|
c. |
Attic |
Outside Air |
From system to surroundings |
2. A chemistry teacher claims that the heat content of a
particular substance is 246 kJ/mol. Is the chemistry teacher claiming that the
substance contains heat? Explain what it meant by this claim.
Answer: Hopefully not.
The chemistry
teacher simply means that there are 246 kJ (kilojoules) of internal energy
stored in the bonds between atoms in 1 mole of that substance. Chemistry types
sometimes refer to this form of internal energy as enthalpy or chemical
potential energy. Because it has the potential to be released in the form of
heat during chemical reactions, chemistry teachers occasionally use the
misnomer heat content to describe it. We all would be better
served if we gave up the phrase heat content in favor of enthalpy or chemical potential energy or
internal energy or ... .
3. Explain why high quality thermos bottles have a vacuum
lining as a major component of their insulating ability.
Answer:
Conduction and
convection are heat transfer methods which depend upon the presence of
materials to transfer heat. By lining a thermos bottle with a vacuum lining,
energy cannot escape the contents of the bottle by two of the three forms of
heat transfer.