Electric Fields and Conductors
We have previously shown in Lesson 4 that any charged object
- positive or negative, conductor or insulator - creates an electric field that
permeates the space surrounding it. In the case of conductors there are a
variety of unusual characteristics about which we could elaborate. Recall from
Lesson 1 that a conductor is material that allows electrons to move
relatively freely from atom to atom. It was emphasized that when a conductor acquires
an excess charge, the excess charge moves about and distributes itself about
the conductor in such a manner as to reduce the total amount of repulsive
forces within the conductor. We will explore this in more detail in this
section of Lesson 4 as we introduce the idea of electrostatic equilibrium. Electrostatic
equilibrium is the condition established by charged conductors in which the excess
charge has optimally distanced itself so as to reduce the total amount of
repulsive forces. Once a charged conductor has reached the state of
electrostatic equilibrium, there is no further motion of charge about the
surface.
Electric
Fields Inside of Charged Conductors
Charged conductors that have reached electrostatic
equilibrium share a variety of unusual characteristics. One characteristic of a
conductor at electrostatic equilibrium is that the electric field
anywhere beneath
the surface of a
charged conductor is zero. If an electric field did exist beneath the surface
of a conductor (and inside of it), then the electric field would exert a force
on all electrons that were present there. This net force would begin to
accelerate and move these electrons. But objects at electrostatic equilibrium
have no further motion of charge about the surface. So if this were to occur,
then the original claim that the object was at electrostatic equilibrium would
be a false claim. If the electrons within a conductor have assumed an equilibrium
state, then the net force upon those electrons is zero. The electric field
lines either begin or end upon a charge and in the case of a conductor, the
charge exists solely upon its outer surface. The lines extend from this surface
outward, not inward. This of course presumes that our conductor does not
surround a region of space where there was another charge.
To illustrate this characteristic, let's consider the space
between and inside of two concentric, conducting cylinders of different radii
as shown in the diagram at the right. The outer cylinder is charged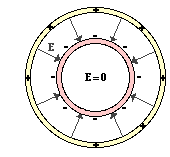 
positively. The inner cylinder is charged negatively. The electric field
about the inner cylinder is directed towards the negatively charged cylinder.
Since this cylinder does not surround a region of space where there is another
charge, it can be concluded that the excess charge resides solely upon the
outer surface of this inner cylinder. The electric field inside the inner
cylinder would be zero. When drawing electric field lines, the lines would be
drawn from the inner surface of the outer cylinder to the outer surface of the
inner cylinder. For the excess charge on the outer cylinder, there is more to
consider than merely the repulsive forces between charges on its surface. While
the excess charge on the outer cylinder seeks to reduce repulsive forces
between its excess charge, it must balance this
with the tendency to be attracted to the negative charges on the inner
cylinder. Since the outer cylinder surrounds a region that is charged, the
characteristic of charge residing on the outer surface of the conductor does
not apply.
This concept of the electric field being zero inside of a
closed conducting surface was first demonstrated by Michael Faraday, a 19th
century physicist who promoted the field theory of electricity. Faraday
constructed a room within a room, covering the inner room with a metal foil. He
sat inside the inner room with an electroscope and charged the surfaces of the
outer and inner room using an electrostatic generator. While sparks were seen
flying between the walls of the two rooms, there was no detection of an
electric field within the inner room. The excess charge on the walls of the
inner room resided entirely upon the outer surface of the room. Today, this
demonstration is often repeated in physics demonstration shows at museums and
universities.
The inner room with the conducting frame that protected
Faraday from the static charge is now referred to as a Faraday's
cage. The cage serves to shield whomever and whatever
is on the inside from the influence of electric fields. Any closed, conducting
surface can serve as a Faraday's cage, shielding whatever it surrounds from the
potentially damaging effects of electric fields. This principle of shielding is commonly
utilized today as we protect delicate electrical equipment by enclosing them in
metal cases. Even delicate computer chips and other components are shipped
inside of conducting plastic packaging that shields the chips from potentially
damaging effects of electric fields. This is one more example of "Physics
for Better Living."
Electric
Fields are Perpendicular to Charged Surfaces
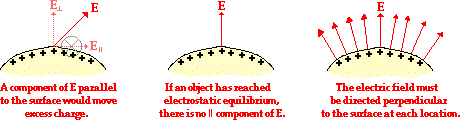
A second characteristic of conductors at
electrostatic equilibrium is that the electric field upon the surface of the
conductor is directed entirely perpendicular to the surface. There cannot be a
component of electric field (or electric force) that is parallel to the
surface. If the conducting object is spherical, then this means that the
perpendicular electric field vectors are aligned with the center of the sphere. If the object is irregularly
shaped, then the electric field vector at any location is perpendicular to a
tangent line drawn to the surface at that location.
Understanding why this characteristic is true demands an
understanding of vectors, force and motion. The motion of electrons, like any
physical object, is governed by Newton's laws. One
outcome of Newton's laws was that unbalanced forces cause objects to accelerate in
the direction of the unbalanced force and a balance of forces causes objects to
remain at equilibrium. This truth provides 
the foundation for the rationale behind why electric fields must be
directed perpendicular to the surface of conducting objects. If there were a
component of electric field directed parallel to the surface, then the excess
charge on the surface would be forced into accelerated motion by this
component. If a charge is set into motion, then the object upon which it is on
is not in a state of electrostatic equilibrium. Therefore, the electric field
must be entirely perpendicular to the conducting surface for objects that are
at electrostatic equilibrium. Certainly a conducting object that has recently
acquired an excess charge has a component of electric field (and electric
force) parallel to the surface; it is this component that acts upon the newly
acquired excess charge to distribute the excess charge over the surface and
establish electrostatic equilibrium. But once reached, there is no longer any
parallel component of electric field and no longer any motion of excess charge.
Electric Fields and Surface Curvature
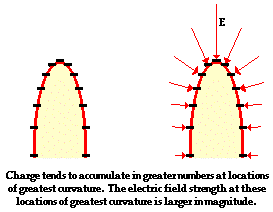
A third characteristic of conducting objects at electrostatic
equilibrium is that the electric fields are strongest at locations along the
surface where the object is most curved. The curvature of a surface can range
from absolute flatness on one extreme to being curved to a blunt point on the other
extreme.
A flat location has no curvature and is characterized by
relatively weak electric fields. On the other hand, ablunt point has a high degree
of curvature and is characterized by relatively strong electric fields. 
A sphere is uniformly shaped with the same curvature at every location
along its surface. As such, the electric field strength on the surface of a
sphere is everywhere the same.
To understand the rationale for this third characteristic, we
will consider an irregularly shaped object that is negatively charged. Such an
object has an excess of electrons. These electrons would distribute themselves
in such a manner as to reduce the effect of their repulsive forces. Since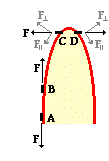 
electrostatic forces vary inversely with the square of the distance,
these electrons would tend to position themselves so as to increase their
distance from one another. On a regularly shaped sphere, the ultimate distance
between every neighboring electron would be
the same. But on an irregularly shaped object, excess electrons would tend to
accumulate in greater density along locations of greatest curvature. Consider
the diagram at the right. Electrons A and B are located along a flatter section
of the surface. Like all well-behaved electrons, they repel each other. The
repulsive forces are directed along a line connecting charge to charge, making
the repulsive force primarily parallel to the surface. On the other hand,
electrons C and D are located along a section of the surface with a sharper
curvature. These excess electrons also repel each other with a force directed
along a line connecting charge to charge. But now the force is directed at a
sharper angle to the surface. The components of these forces parallel to the
surface are considerably less. A majority of the repulsive force between
electrons C and D is directed perpendicular to the surface.
The parallel components of these repulsive forces are what
cause excess electrons to move along the surface of the conductor. The
electrons will move and distribute themselves until electrostatic equilibrium
is reached. Once reached, the resultant of all parallel components on any given
excess electron (and on all excess electrons) will add up to zero. All the
parallel components of force on each of the electrons must be zero since the
net force parallel to the surface of the conductor is always zero (the secondcharacteristicdiscussed above). For the same
separation distance, the parallel component of force is greatest in the case of
electrons A and B. So to acquire this balance of parallel forces, electrons A
and B must distance themselves further from each other than electrons C and D.
Electrons C and D on the other hand can crowd closer together at their location
since that the parallel component of repulsive forces is less. In the end, a
relatively large quantity of charge accumulates on the locations of greatest
curvature. This larger quantity of charge combined with the fact that their
repulsive forces are primarily directed perpendicular to the surface results in
a considerably stronger electric field at such locations of increased curvature.
The fact that surfaces that are sharply curved to a blunt
edge create strong electric fields is the underlying principle for the use of
lightning rods. In the next section of Lesson 4, we will explore the
phenomenon of lightning discharge and the use of lightning rods to prevent
lightning strikes.
Check Your Understanding
Use your understanding to answer the following questions.
When finished, click the button to view the answers.
1. Suppose that the sphere of a Van de Graaff generator gathers a charge. Then the motor is
turned off and the sphere is allowed to reach electrostatic equilibrium. The
charge ___.
a. resides both on
its surface and throughout its volume
b. resides mostly inside
the sphere and only emerges outside when touched
c. resides only on
the surface of the sphere
Answer: C
When a
"closed" conductor becomes charged, the excess of charge accumulates
on the outer surface of the conductor. Since the generator has been turned off,
there is no source of charge inside of it. All the charge resides on the
outside of the dome.
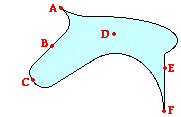2. Describe the electric field strength at the six labeled locations of the irregularly shaped charged
object at the right. Use the phrases "zero," "relatively
weak," "moderate," and relatively strong" as your
descriptions.
Answers:
A, F are relatively strong since they're the most
pointed locations on the conductor's surface.
B, E are relatively weak since they're at the
least curved (most flat) locations on the conductor's surface.
C is of moderate strength since it is at a
location with some curvature but not an extreme amount.
D is 0 since it is at a
location under the surface of the conductor; electric fields are zero inside of
conductors.
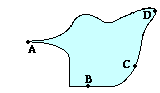3. A diagram of an irregularly shaped charged conductor is shown at the
right. Four locations along the surface are labeled -
A, B, C, and D. Rank these locations in increasing order of the strength of
their electric field, beginning with the smallest electric field.
Answer: B < C < D < A
For conducting
surfaces, electric fields are strongest at locations where the curvature is the
greatest. A projection (such as at point A) is the extreme case of lots of
curvature. A flat section of a surface (such as point B) is on the opposite
extreme with with no curvature. So point B
is listed first and point A is listed last. Since point D is on a section of
the surface which curves more than point C's section, the ordering of the final
two locations is point C < point D.
4. Consider the diagram of the thumbtack shown at the right. Suppose
that the thumbtack becomes positively charged. Draw the electric field lines
surrounding the thumbtack.
See electric field line diagram.
5. Diagram the electric field lines for the following configuration of
two objects. Place arrows on your field lines.
6. A favorite physics
demonstration used with the Van de Graaff generator
involves slowly approaching the dome holding a paper clip stretched towards the
device. Why does the demonstrator not become toast when approaching the machine
with the blunt edge of the paper clip protruding forward?
Answer:
An uncoiled paper
clip becomes an object with a blunt edge with extreme curvature at its tip.
This extreme curvature creates strong electric fields around its surface. The
strength of the electric field is great enough to ionize the air between the
paper clip and the Van de Graaffdome. This
provides a conducting path from the dome to the clip. Charge that normally
accumulates on the dome now flows through the ionized air and is grounded
through the demonstrator. Rather than experiencing a sudden discharge of large
quantities of charge, there is a gradual non-harmful (so he claims) flow of
charge off the dome.
7. TRUE or FALSE:
Lightning
rods are placed on homes to protect them from lightning. They work because the
electric field is weak around the lightning rods; thus, there is little flow of
charge between the lightning rods/home and the charged clouds.
Answer: False
Electric fields
are very strong along the sharply curved or blunt edges of lightning rod. This
creates strong electric fields. To find out why they prevent lightning strikes,
you'll have to read the next section of Lesson 4.
Electric Field Line Diagram for Question #4:
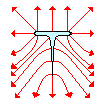
The above diagram was not created by a Field Plotting
software program; it would certainly look better if it had been. Your answer
may look different (especially when the details are compared) but it should
share the following general characteristics with the diagram given here:
· The electric
field lines should be directed from the positively charged thumbtack to the
extremities of the page. Each field line MUST have an arrowhead on it to
indicate such directions.
· All electric
field lines should be perpendicular to the surface of the thumbtack at the
locations where the lines and the thumbtack meet.
· There should
be more lines concentrated at the pointed extremity of the thumbtack and the
two sharply curved sections and fewer lines along the flatter sections of the
thumbtack.
Return to Question #4
Electric Field Line Diagram for Question #5:
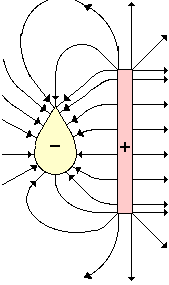
Once more, the above diagram was not created by a Field
Plotting software program; it would likely look better if it had been. Your
answer may look different (especially when the details are compared) but it
should share the following general characteristics with the diagram given here:
· The field
lines should be directed from + to - or from the edge of the page to the - or
from + to the edge of the page. Each field line MUST have an arrowhead on it to
indicate such directions.
· At the
surface of either object, the field lines should be directed perpendicular to
the surface.
· There should
be more lines at the sharply curved and pointed surfaces of the objects and
less lines at the flatter sections.