Newton's Laws and the Electrical Force
The attractive or repulsive interaction between any two
charged objects is an electric force. Like any
force, its effect upon objects is described by Newton's
laws of motion. The electric force - Felect - joins
the long list of other forces that can act upon objects. Newton's laws are
applied to analyze the motion (or lack of motion) of objects under the
influence of such a force or combination of forces. The analysis usually begins
with the construction of a free-body diagram in which
the type and direction of the individual forces are represented by vector
arrows and labeled according to type. The magnitudes of the forces are then
added as vectors in order to determine the resultant sum, also known as the net force. The net force can then be used to determine
the acceleration of the object.
In some instances, the goal of the analysis is not to
determine the acceleration of the object. Instead, the free-body diagram is
used to determine the spatial separation or charge of two objects that are at static
equilibrium. In this case, the free-body diagram is
combined with an understanding of vector principles in order to determine some
unknown quantity in the midst of a puzzle involving geometry, trigonometry and
Coulomb's law. In this last section of Lesson 3, we will explore both types of
applications of Newton's laws to static electricity phenomenon.
Electric
Force and Acceleration
Suppose that a rubber balloon and a plastic golf tube are
both charged negatively by rubbing them with animal fur. Suppose that the
balloon is tossed up into the air and the golf tube is held beneath it in an
effort to levitate the balloon in midair. This goal would be
accomplished when the spatial separation between charged objects is adjusted
such that the downward gravity force (Fgrav) and the upward electric
force (Felect) are balanced. This would present a difficult task of
manipulation as the balloon would constantly move from side to side and up and
down under the influences of both the gravity force and the electric force.
When the golf tube is held too far below the balloon, the balloon would fall
and accelerate downward. This would in turn decrease the separation distance
and lead to an increase in the electric force. As the Felect increases,
it would likely exceed the Fgrav and the
balloon would suddenly accelerate upward. And finally, if the point of
charge on the golf tube is not directly under the point of
charge of the balloon (a likely scenario), the electric force would be exerted
at an angle to the vertical and the balloon would have a sideways acceleration.
The likely result of such an effort to levitate the balloon would be a variety
of instantaneous accelerations in a variety of directions.
Suppose that at some instant in the process of trying to
levitate the balloon, the following conditions existed:
A
0.90-gram balloon with a charge of -75 nC is
located a distance of 12 cm above a plastic golf tube that has a charge of -83
nC.
How could one apply Newton's laws to determine the
acceleration of the balloon at this instant?
Like any problem involving force and acceleration, the
problem would begin with the construction of afree-body
diagram. There are two forces acting upon the balloon. The force of gravity on
the balloon is directed downward. The electric force on the balloon is exerted
upward since the balloon and golf tube are like-charged and the golf tube is
held below the balloon. These two forces are shown in the free-body diagram at
the right. The second step involves determining the magnitude of these two
forces. The force of gravity is determined by multiplying the mass (in
kilograms) by the acceleration of gravity.
Fgrav =
m • g = (0.00090 kg) • (9.8 m/s/s)
Fgrav = 8.82 x 10-3 N, down
The electric force is determined using Coulomb's
law. As shown below, the appropriate unit on
charge is the Coulomb (C) and the appropriate unit on distance is meters (m).
Use of these units will result in a force unit of the Newton. The demand for
these units emerges from the units on Coulomb's constant.
Felect =
k • Q1 • Q2 /d2
Felect = (9 x 109 N•m2/C2)
• (-75 x 10-9 C) • (-83 x 10-9 C) /
(0.12)2
Felect = 3.89 x 10-3 N, up
The net force is the vector sum of these two forces. The
upward and downward forces are added together as vectors.
Fnet =
·F = Fgrav (down) + Felect (up)
Fnet = 8.82 x 10-3 N, down +
3.89 x 10-3 N, up
Fnet = 4.93 x 10-3 N, down
The final step of this problem involves the use of Newton's
second law to determine the acceleration of the object. The acceleration is the
net force divided by the mass (in kilograms).
a = Fnet /
m = (4.93 x 10-3 N,
down) / (0.00090 kg)
a = 5.5 m/s/s, down
The above analysis illustrates how Newton's law and Coulomb's
law can be applied to determine an instantaneous acceleration. The next
analysis involves a case in which two objects are in a state of static
equilibrium.
Electric
Force and Static Equilibrium
Suppose that two rubber balloons are hung from the ceiling by
two long strings such that they hang
vertically. Then suppose that each balloon is given 10 average-strength
rubs with animal fur. The balloons, having a greater attraction for electrons
than animal fur, would acquire a negative charge. The balloons would have the
same type of charge and they would subsequently repel each other. The result of
their repulsion is that the strings and suspended balloons would now make an
angle with the vertical. The angle of the string with the vertical would be
mathematically related to the quantity of charge on the balloons. As the
balloons acquire a greater quantity of charge, the force of repulsion between
them would increase and the angle that the string makes with the vertical would
also increase. Like any situation involving electrostatic force, this situation
can be analyzed using vector principles and Newton's laws.
Suppose that the following conditions existed.
Two
1.1-gram balloons are suspended from 2.0-meter long strings and hung from the
ceiling. They are then rubbed ten times with animal fur to impart an identical
charge Q to each balloon. The balloons repel each other and each string is
observed to make an angle of 15 degrees with the vertical. Determine the
electric force of repulsion, the charge on each balloon (assumed to be
identical), and the quantity of electrons transferred to each balloon as a
result of 10 rubs with animal fur.
Because of the complexity of the physical situation, it would
be wise to represent it using a diagram. The diagram will serve as a means of
identifying the known information for this situation. The diagram below depicts
the two balloons with the string of length L and the
angle "theta". The mass (m) of the balloons is known; it is expressed here in kilogram (the
standard unit of mass). The distance between the balloons (a variable in
Coulomb's law) is marked on the diagram and represented by the variable d. The vertical line extending from the pivot point on the ceiling is
drawn; this vertical line is one side of a right triangle formed by the
horizontal line connecting the balloons and the string extending from balloon
to ceiling. This right triangle will be useful as we analyze the situation
using vector principles. Note that the vertical line bisects the line segment
connecting the balloons; thus, one side of the right triangle has a distance of d/2.
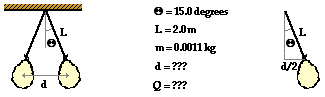
The application of Newton's laws to this situation begins
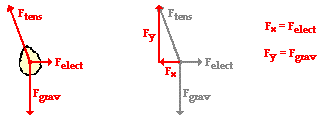
with the construction of a free-body diagram for one of the balloons. There are
three forces acting upon the balloons: the tension force, the force of gravity
and the electrostatic force of repulsion. These three forces are represented
for the balloon on the right. (See diagram below.) Note that the tension force
is directed at an angle to the vertical. In physics, such situations are
treated by resolving the force vector into horizontal and vertical components.
This is shown below; the components are labeled as Fx and Fy. These
components are related to the angle that the string makes with the vertical by
trigonometric functions. Since the balloon is at equilibrium, the forces that
act upon the balloon must balance each other. This would mean that the vertical
component of the tension force (Fy) must balance the downward
force of gravity (Fgrav). And the
horizontal component of the tension force (Fx) must balance the rightward
electrostatic force (Felect).
Since the mass of the balloon is known, the force of gravity
acting upon it can be determined.
Fgrav =
m •g = (0.0011 kg) • (9.8 m/s/s)
Fgrav = 0.01078 N
The force of gravity is equal to the vertical component of
the tension force (Fy = 0.0108 N ). The Fycomponent
is related to the Fx component
and the angle theta by the tangent function. This relationship can
be used to determine the horizontal component of the tension force. The work is
shown below.
Tangent(theta) = opposite
side/adjacent side
Tangent(theta) = Fx / Fy
Tangent(15
degrees) = Fx / (0.01078 N)
Fx = (0.01078 N) • Tangent(15
degrees)
Fx = 0.00289 N
The horizontal component of the tension force is equal to the
electrostatic force. Thus,
Felect =
0.00289 N
Now that the electrostatic force has been determined using
Newton's laws and vector principles, Coulomb's law can now be applied to
determine the charge on the balloon.
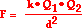
It is assumed that the balloons have the same quantity of
charge since they are charged in the same manner with 10 average-strength rubs.
Since Q1 is equal to Q2, the equation can be
rewritten as
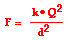
This equation can be algebraically rearranged in order to
solve for Q. The steps are shown below.
F • d2 =
k • Q2
Q2 = F • d2 / k
Q = SQRT(F • d2 / k)
The value of d must be known to complete the solution. This
demands that the right triangle be analyzed in order to determine the length of
the side opposite the 15-degree angle. This length is one-half the distance d.
Since the length of the hypotenuse is known, the sine function is used.
Sine(Theta) = opposite side /
hypotenuse side
Sine(15 degrees) =
opposite side / (2.0 m)
opposite side
= (2.0 m) • Sine(15 degrees)
opposite side
= d/2 = 0.518 m
Doubling this distance yields a value of d of 1.035
m. Now substitutions can be made in order to determine the value of Q.
Q = SQRT(F • d2 / k)
Q = SQRT [(0.00289 N) • (1.035 m)2 / (9 x 109 N•m2/C2)]
Q = 5.87 x 10-7 C (negative)
The charge on an object is related to the number of excess
(or deficient) electrons in the object. Using the charge of a single electron
(-1.6 x 10-19 C), the number of electrons on this object can
be determined:
# excess electrons =
(-5.87 x 10-7 C) / (-1.6 x 10-19 C/electron)
# excess electrons = 3.67 x 1012 electrons
During the charging process, more than three trillion
electrons were transferred from the animal fur to each of the balloons. Wow!
Configurations
of Three or More Charges
In each of the examples above, we have explored the
interaction of two charged objects. Newton's laws and Coulomb's law were
combined to analyze the situations. But what if there are three or more charges
present? Coulomb's law can only consider the interaction between Q1 and Q2.
Does the law for electric force have to be rewritten to account for a Q3?
No!
Electrical forces result from mutual interactions between two
charges. In situations involving three or more charges, the electric force on a
single charge is merely the result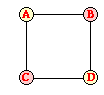 
of the combined effects of each individual charge interaction of that
charge with all other charges. If a particular charge encounters two or more
interactions, then the net electric force is the vector sum of those individual
forces. As an example of this approach, suppose that four charges (A, B, C, and
D) are present and that they are spatially arranged to form a square. Charges A
and D are both negatively charged and occupy opposite corners of the square and
Charges B and C are both positively charged and occupy the remaining two
corners as shown. If one is concerned with the net electric force acting upon
charge A, then the electric forces between A and each of the other three
charges must be calculated. That is, FBA, FCA and FDA must first
be determined by the application of Coulomb's law to each of these pairs of
charges. The notation FBA is used to denote the force
of B on A.
FBA = k • QA • QB / dBA2
FCA = k • QA • QC / dCA2
FDA = k • QA • QD / dDA2
The direction of each of these three forces can be determined
by applying the basic rules of charge interaction: oppositely charged objects
attract and like-charged objects repel. Applied to this scenario, one would
reason that the forces FBA, FCA and FDA are
directed as shown in the diagram below. Charge B attracts A and Charge C attracts A since these are pairs of
oppositely charged objects. But Charge D repels A since they are a pair of
like-charged objects.
So the magnitudes of the individual forces are determined
through Coulomb's law calculations. The direction of the individual forces are
determined by applying the rules of charge interactions. And once the magnitude
and direction of the three force vectors are known, the three vectors can be
added using rules of vector addition in order
to determine the net electric force. This is illustrated in the diagram above.
Check Your Understanding
Use your understanding of charge to answer the following
questions. When finished, click the button to view the answers.
1. A positively charged object with a charge of +85 nC is being used to balance the downward force of
gravity on a 1.8-gram balloon that has a charge of -63 nC. How high above the
balloon must the object be held in order to balance the balloon? (NOTE: 1 nC = 1 x 10-9 C)
Answer: 0.052 meters
Given:
Q1 =
+8.5 x 10-8 C
Q2 = -6.3 x 10-8 C
m = 0.0018 kg
Use the mass to
determine the force of gravity (m • g). The force of gravity on the balloon is
0.0176 N. Thus, the upward electrical force is 0.0176 N. Now that F, Q1,
and Q2 are known, Coulomb's law can be used to determine the
distance d in the equation. Algebraic rearrangement leads to d = Sqrt [ (k• Q1• Q2) / F ]. Substitution
leads to the answer.
2. Balloon A and Balloon B are charged in a like manner by
rubbing with animal fur. Each acquires an excess of 25 trillion electrons. If
the mass of the balloons is 1 gram, then how far below Balloon B must Balloon A
be held in order to levitate Balloon B? Assume the balloons act as point
charges.
Answer: 3.83 meters
Begin by determining the Q of the balloons.
Q1 = Q2 = # of excess electrons
• Qelectron = 4.0 x 10-6 C.
The force of gravity of the balloons is m • g or 0.0098 N.
To levitate the top balloon over the bottom balloon, the
electrical force of repulsion must equal the force of gravity on the top
balloon. Thus Felect = 0.0098 N.
Now that Q1,
Q2, and F are known, Coulomb's law can be used to determine the
distance d. Algebraic rearrangement leads to d = Sqrt [ (k• Q1 •
Q2 ) / F ]. Substitution leads to the answer.
3. Two 1.2-gram balloons are suspended from light strings
attached to the ceiling at the same point. The net charge on the balloons is
-540 nC. The balloons are distanced 68.2 cm apart
when at equilibrium. Determine the length of the string.
Answer: 78.8 cm
Like the example problem above, it is best to begin with a
sketch of the situation and a free-body diagram.
Q1 and Q2 are known to be
-5.4x10-7 C.
The separation distance is 0.682 m.
Using Coulomb's law and values of Q1, Q2,
and d, the electric force can be found to be 5.64x10-3 N.
The force of gravity is m • g or 0.0118 N.
From the FBD and the sketch, one sees that the
tangent(theta) = Felect /
Fgrav = (5.64x10-3 N) / (0.0118 N) = 0.4798.
Thus, theta (the angle with the vertical) is 25.6 degrees.
From a distance
triangle, one sees that sin(theta) = 0.5 • d / L
Substituting theta and d into this equation leads to the answer
4. ZINGER: Three charges
are placed along the X-axis. Charge A is a +18 nC charge
placed at the origin. Charge B is a -27 nC charge
placed at the 60 cm location. Where along the axis (at what x-coordinate?) must
positively charged C be placed in order to be at equilibrium?
Answer: x = -267 cm
Some reasoning would lead to the conclusion that C must be
located to the left of A so that the repulsion interaction with B is balanced
by the attractive interaction with A. Thus, the distance from A to C can be
called x and the distance from B to C can be called 0.6 + x (where x is the
absolute value of the coordinate position (in meters).
Expressions for
FAC and FBC can be written
|
FAC = k • QA •
QC / (dAC)2 |
FBC = k • QB • QC /
(dBC)2 |
and set equal to each
other since objects at equilibrium have balanced forces. Thus
k • QA •
QC / (dAC)2 =
k • QB • QC / (dBC)2
The equation can be simplified by canceling k and QC.
Thus,
QA /
(dAC)2 = QB /
(dBC)2
Substitute x and 0.6 + x into this equation:
QA /
x2 = QB / ( 0.6 +
x )2
Then solve for x
by taking the square root of each side and substituting the Q values into the
equation.