Weightlessness in Orbit
Astronauts who are orbiting the Earth often experience
sensations of weightlessness. These sensations experienced by orbiting
astronauts are the same sensations experienced by anyone who has been
temporarily suspended above the seat on an amusement park ride. Not only are
the sensations the same (for astronauts and roller coaster riders), but the
causes of those sensations of weightlessness are also the same. Unfortunately
however, many people have difficulty understanding the causes of
weightlessness.
What Do You Believe?
The cause of weightlessness is quite simple to understand.
However, the stubbornness of one's preconceptions on the topic often stand in
the way of one's ability to understand. Consider the following multiple choice
question about weightlessness as a test of your preconceived notions on the
topic:
|
Test your preconceived notions about weightlessness: Astronauts
on the orbiting space station are weightless because... a. there is no gravity in space and they
do not weigh anything. b. space is a vacuum and there is no gravity in a vacuum. c. space is a vacuum and there is no air resistance in a
vacuum. d. the astronauts are far from Earth's surface at a
location where gravitation has a minimal effect. |
None of these are appropriate reasons for the weightless
sensations experienced by orbiting astronauts. Continue reading this part of
Lesson 4 to find out the real reason.
If you believe in any one of the above statements, then it might take a little
rearrangement and remapping of your brain to understand the real cause of
weightlessness. As is the case on many topics in Physics, some unlearning must
first be done before doing the learning. Put another way: it's not what you
don't know that makes learning physics a difficult task; it's what you do know
that makes learning physics a difficult task. So if you do have a preconception
(or a strong preconception) about what weightlessness is, you need to be aware
of that preconceived idea. And as you consider the following alternative
conception about the meaning of weightlessness, evaluate the reasonableness and
logic of the two competing ideas.
Contact
versus Non-Contact Forces
Before understanding weightlessness, we will have to review two
categories of forces - contact forces and action-at-a-distance forces. As you sit in a
chair, you experience two forces - the force of the Earth's gravitational field
pulling you downward toward the Earth and the force of the chair pushing you
upward. The upward chair force is sometimes referred to as a normal force and results
from the contact between the chair top and your bottom end. This normal force
is categorized as a contact force. Contact forces can only
result from the actual touching of the two interacting objects - in this case,
the chair and you. The force of gravity acting upon your body is not a contact
force; it is often categorized as an action-at-a-distance force. The 
force of gravity is the result of your centerof
mass and the Earth's center of mass
exerting a mutual pull on each other; this force would even exist if you were
not in contact with the Earth. The force of gravity does not require that the
two interacting objects (your body and the Earth) make physical contact; it can
act over a distance through space. Since the force of gravity is not a contact
force, it cannot be felt through contact. You can never feel the force of gravity
pulling upon your body in the same way that you would feel a contact force. If
you slide across the asphalt tennis court (not recommended), you would feel the
force of friction (a contact force). If you are pushed by a bully in the
hallway, you would feel the applied force (a contact force). If you swung from
a rope in gym class, you would feel the tension force (a contact force). If you
sit in your chair, you feel the normal force (a contact force). But if you are
jumping on a trampoline, even while moving through the air, you do not feel the
Earth pulling upon you with a force of gravity (an action-at-a-distance force).
The force of gravity can never be felt. Yet those forces that result from
contact can be felt. And in the case of sitting in your chair, you can feel the
chair force; and it is this force that provides you with a sensation of weight.
Since the upward normal force would equal the downward force of gravity when at
rest, the strength of this normal force gives one a measure of the amount of gravitational
pull. If there were no upward normal force acting upon your body, you would not
have any sensation of your weight. Without the contact force (the normal
force), there is no means of feeling the non-contact force (the force of
gravity).
Meaning
and Cause of Weightlessness
Weightlessness is simply a sensation experienced by an
individual when there are no external objects touching one's body and exerting
a push or pull upon it. Weightless sensations exist when all contact forces are
removed. These sensations are common to any situation in which you are
momentarily (or perpetually) in a state of free fall. When in free fall, the
only force acting upon your body is the force of gravity - a non-contact force.
Since the force of gravity cannot be felt without any other opposing forces,
you would have no sensation of it. You would feel weightless when in a state of
free fall.
These feelings of weightlessness are common at amusement
parks for riders of roller coasters and other rides in which riders are
momentarily airborne and lifted out of their seats. Suppose that you were
lifted in your chair 
to the top of a very high tower and then your chair was suddenly
dropped. As you and your chair fall towards the ground, you both accelerate at
the same rate - g. Since the chair is unstable, falling at the
same rate as you, it is unable to push upon you. Normal forces only result from
contact with stable, supporting surfaces. The force of gravity is the only
force acting upon your body. There are no external objects touching your body
and exerting a force. As such, you would experience a weightless sensation. You
would weigh as much as you always do (or as little) yet you would not have any
sensation of this weight.
Weightlessness is only a sensation; it is not a reality
corresponding to an individual who has lost weight. As you are free falling on
a roller coaster ride (or other amusement park ride), you have not momentarily
lost your weight. Weightlessness has very little to do with weight and mostly
to do with the presence or absence of contact forces. If by "weight"
we are referring to the force of gravitational attraction to the Earth, a
free-falling person has not "lost their weight;" they are still
experiencing the Earth's gravitational attraction. Unfortunately, the confusion
of a person's actual weight with one's feeling of weight is the source of many
misconceptions.
Scale
Readings and Weight
Technically speaking, a scale does not measure one's weight.
While we use a scale to measure one's weight, the scale reading is actually 
a measure of the upward force applied by the scale to balance the
downward force of gravity acting upon an object. When an object is in a state
of equilibrium (either at rest or in motion at constant speed), these two
forces are balanced. The upward force of the scale upon the person equals the
downward pull of gravity (also known as weight). And in this instance, the
scale reading (that is a measure of the upward force) equals the weight of the
person. However, if you stand on the scale and bounce up and down, the scale
reading undergoes a rapid change. As you undergo this bouncing motion, your
body is accelerating. During the acceleration periods, the upward force of the
scale is changing. And as such, the scale reading is changing. Is your weight
changing? Absolutely not! You weigh as much (or as little) as you always do.
The scale reading is changing, but remember: the SCALE DOES NOT MEASURE YOUR
WEIGHT. The scale is only measuring the external contact force that is being
applied to your body.
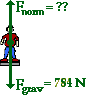
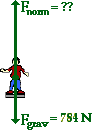
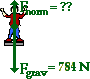
Now consider Otis L. Evaderz who
is conducting one of his famous elevator experiments. He stands on a bathroom
scale and rides an elevator up and down. As he is accelerating upward and
downward, the scale reading is different than when he is at rest and traveling
at constant speed. When he is accelerating, the upward and downward forces are
not equal. But when he is at rest or moving at constant speed, the opposing
forces balance each other. Knowing that the scale reading is a measure of the
upward normal force of the scale upon his body, its value could be predicted
for various stages of motion. For instance, the value of the normal force (Fnorm) on Otis's 80-kg body could be predicted
if the acceleration is known. This prediction can be made by simply applying
Newton's second law as discussed . As an illustration of the use of Newton's second law to determine the
varying contact forces on an elevator ride, consider the following diagram. In
the diagram, Otis's 80-kg is traveling with constant speed (A), accelerating
upward (B), accelerating downward (C), and free falling (D) after the elevator
cable snaps.
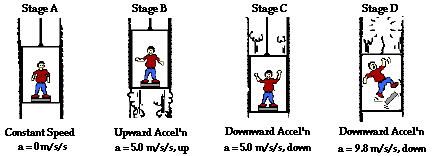
In each of these cases, the upward contact force (Fnorm) can be determined using a free-body
diagram and Newton's second law. The interaction of the two forces - the upward
normal force and the downward force of gravity - can be thought of as a
tug-of-war. The net force acting upon the person indicates who wins the
tug-of-war (the up force or the down force) and by how much. A net force of 100-N, up indicates
that the upward force "wins" by an amount equal to 100 N. The
gravitational force acting upon the rider is found using the equation Fgrav = m*g.
|
Stage A
|
Stage B
|
Stage C
|
Stage D
|
|
Fnet = m*a Fnet = 0 N |
Fnet = m*a Fnet = 400 N, up |
Fnet = m*a Fnet = 400 N, down |
Fnet = m*a Fnet = 784 N, down |
|
Fnorm equals Fgrav Fnorm = 784 N |
Fnorm > Fgrav by 400 N Fnorm = 1184 N |
Fnorm < Fgrav by 400 N Fnorm = 384 N |
Fnorm < Fgrav by 784 N Fnorm = 0 N |
The normal force is greater than the force of gravity when
there is an upward acceleration (B), less than the force of gravity when there
is a downward acceleration (C and D), and equal to the force of gravity when
there is no acceleration (A). Since it is the normal force that provides a
sensation of one's weight, the elevator rider would feel his normal weight in
case A, more than his normal weight in case B, and less than his normal weight
in case C. In case D, the elevator rider would feel absolutely weightless;
without an external contact force, he would have no sensation of his weight. In
all four cases, the elevator rider weighs the same amount - 784 N. Yet the
rider's sensation of his weight is fluctuating throughout the elevator ride.
Weightlessness
in Orbit
Earth-orbiting astronauts are weightless for the same reasons
that riders of a free-falling amusement park ride or a free-falling elevator
are weightless. They are weightless because there is no external contact force
pushing or pulling upon their body. In each case, gravity is the only force
acting upon their body. Being an action-at-a-distance force, it cannot be felt
and therefore would not provide any sensation of their weight. But for certain,
the orbiting astronauts weigh something; that is, there is a force of gravity
acting upon their body. In fact, if it were not for the force of gravity, the
astronauts would not be orbiting in circular motion. It is the force of gravity
that supplies the centripetal force requirement to allow
the inward that is
characteristic of circular motion. The force of gravity is the only force
acting upon their body. The astronauts are in free-fall. Like the falling
amusement park rider and the falling elevator rider, the astronauts and their
surroundings are falling towards the Earth under the sole influence of gravity.
The astronauts and all their surroundings - the space station with its contents
- are falling towards the Earth without colliding into it. Their tangential velocity allows them to remain in orbital motion while
the force of gravity pulls them inward.
Many students believe that orbiting astronauts are weightless
because they do not experience a force of gravity. So to presume that the
absence of gravity is the cause of the weightlessness experienced by orbiting
astronauts would be in violation of circular motion principles. If a person
believes that the absence of gravity is the cause of their weightlessness, 
then that person is hard-pressed to come up with a reason for why the
astronauts are orbiting in the first place. The fact is that there must be a
force of gravity in order for there to be an orbit.
One might respond to this discussion by adhering to a second
misconception: the astronauts are weightless because the force of gravity is
reduced in space. The reasoning goes as follows: "with less gravity, there
would be less weight and thus they would feel less than their normal
weight." While this is partly true, it does not explain their sense of
weightlessness. The force of gravity acting upon an astronaut on the space
station is certainly less than on Earth's surface. But how much less? Is it
small enough to account for a significant reduction in weight? Absolutely not!
If the space station orbits at an altitude of approximately 400 km above the
Earth's surface, then the value of g at that location will be reduced from 9.8
m/s/s (at Earth's surface) to approximately 8.7 m/s/s. This would cause an
astronaut weighing 1000 N at Earth's surface to be reduced in weight to
approximately 890 N when in orbit. While this is certainly a reduction in
weight, it does not account for the absolutely weightless sensations that
astronauts experience. Their absolutely weightless sensations are the result of
having "the floor pulled out from under them" (so to speak) as they
are free falling towards the Earth.
Still other physics students believe that weightlessness is
due to the absence of air in space. Their misconception lies in the idea that
there is no force of gravity when there is no air. According to them, gravity
does not exist in a vacuum. But this is not the case. Gravity is a force that
acts between the Earth's mass and the mass of other objects that surround it.
The force of gravity can act across large distances and its effect can even
penetrate across and into the vacuum of outer space. Perhaps students who own
this misconception are confusing the force of gravity with air pressure. Air
pressure is the result of surrounding air particles pressing upon the surface
of an object in equal amounts from all directions. The force of gravity is not
affected by air pressure. While air pressure reduces to zero in a location void
of air (such as space), the force of gravity does not become 0 N. Indeed the
presence of a vacuum results in the absence of air resistance; but this would
not account for the weightless sensations. Astronauts merely feel weightless
because there is no external contact force pushing or pulling upon their body.
They are in a state of free fall.
Check
Your Understanding
1. Otis L. Evaderz is
conducting his famous elevator experiments. Otis stands on a bathroom scale and
reads the scale while ascending and descending the John Hancock building. Otis'
mass is 80 kg. He notices that the scale readings depend on what the elevator
is doing. Use a free-body diagram and Newton's second law of motion to solve
the following problems.
a. What is the scale reading when Otis accelerates upward at
0.40 m/s2?
Answer: Fnorm = 816 N
Fnet = m • a = (80 kg) •
(0.4 m/s/s) = 32 N, up
So the up force (Fnorm) is
32 N greater than Fgrav.
Fgrav = m • g = 784 N, down
Therefore, Fnorm =
816 N.
b. What is the scale reading when Otis is traveling upward at
a constant velocity of at 2.0 m/s?
Answer: Fnorm = 784 N
Fnet = m • a = (80 kg) •
(0 m/s/s) = 0 N (meaning that it is a constant speed motion)
So the up force (Fnorm) is
equal to Fgrav.
Fgrav = m • g = 784 N, down
Therefore, Fnorm =
784 N.
c. As Otis approaches the top of the building, the elevator
slows down at a rate of 0.40 m/s2. Be cautious of the direction of
the acceleration. What does the scale read?
Answer: Fnorm = 752 N
Fnet = m • a = 80 kg • 0.4
m/s/s = 32 N, down and
So the up force (Fnorm) is
32 N less than Fgrav.
Fgrav = m • g = 784 N, down
Therefore, Fnorm =
752 N.
(The acceleration is downwards since the elevator is moving
upwards and slowing down.)
d. Otis stops at the top floor and then accelerates downward
at a rate of 0.40 m/s2. What does the scale read?
Answer: Fnorm = 752 N
Fnet = m • a = (80 kg) •
(0.4 m/s/s) = 32 N, down and
So the up force (Fnorm) is
32 N less than Fgrav.
Fgrav = m • g = 784 N, down
Therefore, Fnorm =
752 N.
e. As Otis approaches the ground floor, the elevator slows
down (an upward acceleration) at a rate of 0.40 m/s2. Be cautious of
the direction of the acceleration. What does the scale read?
Answer: Fnorm = 816 N
Fnet = m • a = (80 kg) •
(0.4 m/s/s) = 32 N, up and
So the up force (Fnorm) is
32 N greater than Fgrav.
Fgrav = m • g = 784 N, down
Therefore, Fnorm =
816 N.
(The acceleration is upwards since the elevator is moving
downwards and slowing down.)
f. Use the results of your calculations above to explain why
Otis fells less weighty when accelerating downward on the elevator and why he
feels heavy when accelerating upward on the elevator.
When accelerating upwards, the contact force (Fnorm) is greater than the usual amount. This
gives Otis the sensation of weighing more than his usual amount. When
accelerating downwards, the contact force (Fnorm)
is less than the normal amount. This gives Otis the sensation of weighing less
than his usual amount. In all cases, Otis' weight is not changing - he still weighs
784 N.