Mathematics of Satellite Motion
The motion of objects is governed by Newton's laws. The same
simple laws that govern the motion of objects on earth also extend to the heavens to govern
the motion of planets, moons, and other satellites. The mathematics that
describes a satellite's motion is the same mathematics presented for circular
motion in earlier topic. In this part of Lesson 4, we will be concerned with
the variety of mathematical equations that describe the motion of satellites.
Orbital Speed Equation
Consider a satellite with mass Msat orbiting a
central body with a mass of mass MCentral. The central
body could be a planet, the sun or some other large mass capable of causing
sufficient acceleration on a less massive nearby object. If the satellite moves
in circular motion, then the net centripetal force acting
upon this orbiting satellite is given by the relationship
Fnet = ( Msat •
v2 ) / R
This net centripetal force is the result of the gravitational
force that attracts the satellite towards the central body and can be
represented as
Fgrav = ( G • Msat • MCentral )
/ R2
Since Fgrav = Fnet, the above expressions for centripetal force and gravitational force
can be set equal to each other. Thus,
(Msat • v2) / R = (G • Msat • MCentral ) / R2
Observe that the mass of the satellite is present on both
sides of the equation; thus it can be canceled by dividing through by Msat. Then both sides
of the equation can be multiplied by R, leaving the
following equation.
v2 =
(G • MCentral ) /
R
Taking the square root of each side, leaves the following
equation for the velocity of a satellite moving about a central body in
circular motion
where G is 6.673 x
10-11 N•m2/kg2, Mcentral is the mass of the central body about which the
satellite orbits, and R is the radius of orbit for the satellite.
The Acceleration Equation
Similar reasoning can be used to determine an equation for
the acceleration of our satellite that is expressed in terms of masses and
radius of orbit. The acceleration value of a satellite is equal to the
acceleration of gravity of the satellite at whatever location that it is
orbiting. In Lesson 3, the equation for the acceleration of gravity
was given as
g = (G • Mcentral)/R2
Thus, the acceleration of a satellite in circular motion
about some central body is given by the following equation
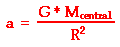
where G is 6.673 x
10-11 N•m2/kg2, Mcentral is the mass of the central body about which the
satellite orbits, and R is the average radius of orbit for the
satellite.
Orbital
Period Equation
The final equation that is useful in describing the motion of
satellites is Newton's form of Kepler's third law. Since the logic behind the
development of the equation has been presented elsewhere, only the equation will be presented here. The period of a satellite (T) and the mean distance from the central body (R) are related by the following equation:
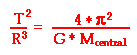
where T is the
period of the satellite, R is the average radius of orbit for the
satellite (distance from center of central planet), and G is 6.673 x 10-11 N•m2/kg2.
There is an important concept evident in all three of these
equations - the period, speed and the acceleration of an orbiting satellite are
not dependent upon the mass of the satellite.
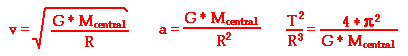
None of these three equations has the variable Msatellite in them. The
period, speed and acceleration of a satellite are only dependent upon the
radius of orbit and the mass of the central body that the satellite is
orbiting. Just as in the case of the motion of projectiles on earth, the mass
of the projectile has no effect upon the acceleration towards the earth and the
speed at any instant. When air resistance is negligible and only gravity is
present, the mass of the moving object becomes a non-factor. Such is the case
of orbiting satellites.
Example
Problems
To illustrate the usefulness of the above equations, consider
the following practice problems.
|
Practice Problem #1 A
satellite wishes to orbit the earth at a height of 100 km (approximately 60
miles) above the surface of the earth. Determine the speed, acceleration and
orbital period of the satellite. (Given: Mearth = 5.98 x 1024 kg, Rearth = 6.37 x 106 m) |
Like most problems in physics, this problem begins by
identifying known and unknown information and selecting the appropriate
equation capable of solving for the unknown. For this problem, the knowns and
unknowns are listed below.
|
Given/Known: R = Rearth + height = 6.47 x 106 m Mearth = 5.98x1024 kg G = 6.673 x 10-11 N m2/kg2 |
Unknown: v = ??? a = ??? T = ??? |
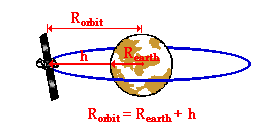Note that the radius of a satellite's orbit can be found from the
knowledge of the earth's radius and the height of the satellite above the
earth. As shown in the diagram at the right, the radius of orbit for a
satellite is equal to the sum of the earth's radius and the height above the
earth. These two quantities can be added to yield the orbital radius. In this
problem, the 100 km must first be converted to 100 000 m before being added to
the radius of the earth. The equations needed to determine the unknown are
listed above. We will begin by determining the orbital
speed of the satellite using the following equation:
v = SQRT [ (G•MCentral ) / R ]
The substitution and solution are as follows:
v = SQRT [ (6.673 x 10-11 N m2/kg2) • (5.98 x 1024 kg) / (6.47 x 106 m) ]
v = 7.85 x 103 m/s
The acceleration can be found from either one of the
following equations:
|
(1) a = (G • Mcentral)/R2 |
(2) a = v2/R |
Equation (1) was derived above. Equation (2) is a general equation for circular motion. Either equation can be used to calculate the acceleration. The use of
equation (1) will be demonstrated here.
a = (G •Mcentral)/R2
a = (6.673 x 10-11 N m2/kg2) • (5.98 x 1024 kg) / (6.47 x 106 m)2
a = 9.53 m/s2
Observe that this acceleration is slightly less than the 9.8
m/s2 value expected on earth's surface. As discussed , the increased distance from the center of the earth lowers the value of g.
Finally, the period can be calculated using the following
equation:
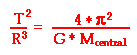
The equation can be rearranged to the following form
T = SQRT [(4 • pi2 • R3) / (G*Mcentral)]
The substitution and solution are as follows:
T = SQRT [(4 • (3.1415)2 • (6.47 x 106 m)3)
/ (6.673 x 10-11 N m2/kg2) • (5.98x1024 kg) ]
T = 5176 s = 1.44 hrs
|
Practice Problem #2 The
period of the moon is approximately 27.2 days (2.35 x 106 s). Determine the radius of the moon's
orbit and the orbital speed of the moon. (Given: Mearth = 5.98 x 1024 kg, Rearth = 6.37 x 106 m) |
Like Practice Problem #2, this problem begins by identifying
known and unknown values. These are shown below.
|
Given/Known: T = 2.35 x 106 s Mearth = 5.98 x 1024 kg G = 6.673 x 10-11 N m2/kg2 |
Unknown: R = ??? v = ??? |
The radius of orbit can be calculated using the following
equation:
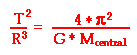
The equation can be rearranged to the following form
R3 = [ (T2 • G • Mcentral)
/ (4 • pi2)
]
The substitution and solution are as follows:
R3 = [ ((2.35x106 s)2 • (6.673 x 10-11 N m2/kg2) • (5.98x1024 kg) ) / (4 • (3.1415)2) ]
R3 = 5.58 x 1025 m3
By taking the cube root of 5.58 x 1025 m3,
the radius can be determined as follows:
R = 3.82 x 108 m
The orbital speed of the satellite can be computed from
either of the following equations:
|
(1) v = SQRT [ (G • MCentral ) / R ] |
(2) v = (2 • pi • R)/T |
Equation (1) was derived above. Equation (2) is a general equation for circular motion. Either equation can be used to calculate the orbital speed; the use of
equation (1) will be demonstrated here. The substitution of values into this
equation and solution are as follows:
v = SQRT [ (6.673 x 10-11 N m2/kg2)*(5.98x1024 kg) / (3.82 x 108 m) ]
v = 1.02 x 103 m/s
|
Practice Problem #3 A
geosynchronous satellite is a satellite that orbits the earth with an orbital
period of 24 hours, thus matching the period of the earth's rotational
motion. A special class of geosynchronous satellites is a geostationary
satellite. A geostationary satellite orbits the earth in 24 hours along an
orbital path that is parallel to an imaginary plane drawn through the Earth's
equator. Such a satellite appears permanently fixed above the same location
on the Earth. If a geostationary satellite wishes to orbit the earth in 24
hours (86400 s), then how high above the earth's surface must it be located?
(Given: Mearth = 5.98x1024 kg, Rearth= 6.37 x 106 m) |
Just as in the previous problem, the solution begins by the
identification of the known and unknown values. This is shown below.
|
Given/Known: T = 86400 s Mearth = 5.98x1024 kg Rearth = 6.37 x 106 m G = 6.673 x 10-11 N m2/kg2 |
Unknown: h = ??? |
The unknown in this problem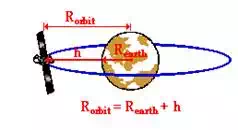 
is the height (h) of the
satellite above the surface of the earth. Yet there is no equation with the
variable h. The solution then involves first finding the
radius of orbit and using this R value and the R of the earth to find the
height of the satellite above the earth. As shown in the diagram at the right,
the radius of orbit for a satellite is equal to the sum of the earth's radius
and the height above the earth. The radius of orbit can be found using the
following equation:
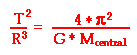
The equation can be rearranged to the following form
R3 = [ (T2 * G * Mcentral)
/ (4*pi2) ]
The substitution and solution are as follows:
R3 = [ ((86400 s)2 • (6.673 x 10-11 N m2/kg2) • (5.98x1024 kg) ) / (4 • (3.1415)2) ]
R3 = 7.54 x 1022 m3
By taking the cube root of 7.54 x 1022 m3,
the radius can be determined to be
R = 4.23 x 107 m
The radius of orbit indicates the distance that the satellite
is from the center of the earth. Now that the radius of orbit has been found, the
height above the earth can be calculated. Since the earth's surface is 6.37 x
106 m from its center (that's the radius of the earth), the satellite must be a height of
4.23 x 107 m
- 6.37 x 106 m = 3.59 x 107 m
above the surface
of the earth. So the height of the satellite is 3.59 x 107 m.
|
|
|
|
|
|
|
Check Your Understanding
1. A satellite is orbiting the earth. Which of the following
variables will affect the speed of the satellite?
a. mass of the satellite
b. height above
the earth's surface
c. mass of the
earth
Answer: b and c
As seen in the
equation v = SQRT(G * Mcentral /
R), the mass of the central body (earth) and the radius of the orbit affect
orbital speed. The orbital radius is in turn dependent upon the height of the
satellite above the earth.
2. Use the information below and the relationship above to
calculate the T2/R3 ratio for
the planets about the Sun, the moon about the Earth, and the moons of Saturn
about the planet Saturn. The value of G is 6.673 x 10-11 N•m2/kg2.
|
Sun |
M = 2.0 x 1030 kg |
|
Earth |
M = 6.0 x 1024 kg |
|
Saturn |
M = 5.7 x 1026 kg |
a.
T2/R3 for
planets about sun
b. T2/R3 for the
moon about Earth
c. T2/R3 for moons
about Saturn
For each case, use the equation T2/ R3=
4*pi2 / (G*Mcentral).
a. Sun T2/ R3= 2.96*10-19
b. Earth T2/ R3= 9.86*10-14
c. Saturn T2/ R3= 1.04*10-15
(All answers in
units of s2 / m3.)
3. One of Saturn's moons is named Mimas. The mean orbital
distance of Mimas is 1.87 x 108 m. The
mean orbital period of Mimas is approximately 23 hours (8.28x104 s). Use
this information to estimate a mass for the planet Saturn.
Using the T and R
values given, the T2/ R3 ratio is 1.05 x 10-15.
This ratio is equal to 4*pi2 / G * Mcentral.
Using the G value and the calculated ratio, the mass of saturn can
be found to be 5.64 x 1026 kg.
close
4. Consider a satellite which is in a low orbit
about the Earth at an altitude of 220 km above Earth's surface. Determine the
orbital speed of this satellite. Use the information given below.
|
G = 6.673 x 10-11 Nm2/kg2 Mearth = 5.98 x 1024 kg Rearth = 6.37 x 106 m |
The orbital
speed can be found using v = SQRT(G*M/R). The R
value (radius of orbit) is the earth's radius plus the height above the earth -
in this case, 6.59 x 106 m. Substituting and solving yields a
speed of 7780
m/s.
5. Suppose the Space Shuttle is in orbit about the earth at
400 km above its surface. Use the information given in the previous question to
determine the orbital speed and the orbital period of the Space Shuttle.
The orbital speed
can be found using v = SQRT(G*M/R). The R value
(radius of orbit) is the earth's radius plus the height above the earth - in
this case, 6.77 x 106 m. Substituting and solving yields a
speed of 7676
m/s.
close