Circular Motion Principles for Satellites

A satellite is any object that is orbiting the earth, sun or other massive body. Satellites can be categorized as natural satellites or man-made satellites. The moon, the planets and comets are examples of natural satellites. Accompanying the orbit of natural satellites are a host of satellites launched from earth for purposes of communication, scientific research, weather forecasting, intelligence, etc. Whether a moon, a planet, or some man-made satellite, every satellite's motion is governed by the same physics principles and described by the same mathematical equations.

A Satellite is a Projectile

The fundamental principle to be understood concerning satellites is that a satellite is a projectile. That is to say, a satellite is an object upon which the only force is gravity. Once launched into orbit, the only 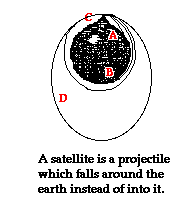force governing the motion of a satellite is the force of gravity. Newton was the first to theorize that a projectile launched with sufficient speed would actually orbit the earth. Consider a projectile launched horizontally from the top of the legendary Newton’s Mountain - at a location high above the influence of air drag. As the projectile moves horizontally in a direction tangent to the earth, the force of gravity would pull it downward. And as mentioned in Lesson 3, if the launch speed was too small, it would eventually fall to earth. The diagram at the right resembles that found in Newton's original writings. Paths A and B illustrate the path of a projectile with insufficient launch speed for orbital motion. But if launched with sufficient speed, the projectile would fall towards the earth at the same rate that the earth curves. This would cause the projectile to stay the same height above the earth and to orbit in a circular path (such as path C). And at even greater launch speeds, a cannonball would once more orbit the earth, but now in an elliptical path (as in path D). At every point along its trajectory, a satellite is falling toward the earth. Yet because the earth curves, it never reaches the earth.

So what launch speed does a satellite need in order to orbit the earth? The answer emerges from a basic fact about the curvature of the earth. For every 8000 meters measured along the horizon of the earth, the earth's surface curves downward by approximately 5 meters. So if you were to look out horizontally along the horizon of the Earth for 8000 meters, you would observe that the Earth curves downwards below this straight-line path a distance of 5 meters. For a projectile to orbit the earth, it must travel horizontally a distance of 8000 meters for every 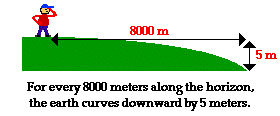5 meters of vertical fall. It so happens that the vertical distance that a horizontally launched projectile would fall in its first second is approximately 5 meters (0.5*g*t²). For this reason, a projectile launched horizontally with a speed of about 8000 m/s will be capable of orbiting the earth in a circular path. This assumes that it is launched above the surface of the earth and encounters negligible atmospheric drag. As the projectile travels tangentially a distance of 8000 meters in 1 second, it will drop approximately 5 meters towards the earth. Yet, the projectile will remain the same distance above the earth due to the fact that the earth curves at the same rate that the projectile falls. If shot with a speed greater than 8000 m/s, it would orbit the earth in an elliptical path. 

Velocity, Acceleration and Force Vectors

The motion of an orbiting satellite can be described by the same motion characteristics as any object in circular motion. The velocity of the satellite would be directed tangent to the circle at every point along its path. The acceleration of the satellite would be directed towards the center of the circle - towards the central body that it is orbiting. And this acceleration is caused by a net force that is directed inwards in the same direction as the acceleration.

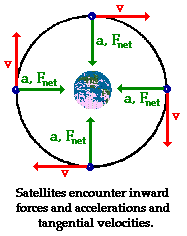
This centripetal force is supplied by gravity - the force that universally acts at a distance between any two objects that have mass. Were it not for this force, the satellite in motion would continue in motion at the same speed and in the same direction. It would follow its inertial, straight-line path. Like any projectile, gravity alone influences the satellite's trajectory such that it always falls below its straight-line, inertial path. This is depicted in the diagram below. 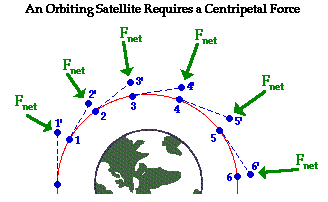Observe that the inward net force pushes (or pulls) the satellite (denoted by blue circle) inwards relative to its straight-line path tangent to the circle. As a result, after the first interval of time, the satellite is positioned at position 1 rather than position 1'. In the next interval of time, the same satellite would travel tangent to the circle in the absence of gravity and be at position 2'; but because of the inward force the satellite has moved to position 2 instead. In the next interval of time, the same satellite has moved inward to position 3 instead of tangentially to position 3'. This same reasoning can be repeated to explain how the inward force causes the satellite to fall towards the earth without actually falling into it.

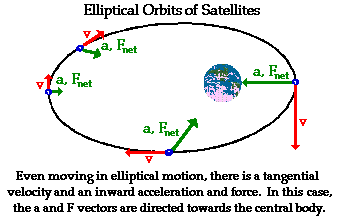
Elliptical Orbits of Satellites

Occasionally satellites will orbit in paths that can be described as ellipses. In such cases, the central body is located at one of the foci of the ellipse. Similar motion characteristics apply for satellites moving in elliptical paths. The velocity of the satellite is directed tangent to the ellipse. The acceleration of the satellite is directed towards the focus of the ellipse. And in accord with Newton's second law of motion, the net force acting upon the satellite is directed in the same direction as the acceleration - towards the focus of the ellipse. Once more, this net force is supplied by the force of gravitational attraction between the central body and the orbiting satellite. In the case of elliptical paths, there is a component of force in the same direction as (or opposite direction as) the motion of the object. such a component of force can cause the satellite to either speed up or slow down in addition to changing directions. So unlike uniform circular motion, the elliptical motion of satellites is not characterized by a constant speed.

In summary, satellites are projectiles that orbit around a central massive body instead of falling into it. Being projectiles, they are acted upon by the force of gravity - a universal force that acts over even large distances between any two masses. The motion of satellites, like any projectile, is governed by Newton's laws of motion. For this reason, the mathematics of these satellites emerges from an application of Newton's universal law of gravitation to the mathematics of circular motion. The mathematical equations governing the motion of satellites.

Check Your Understanding

1. The fact that satellites can maintain their motion and their distance above the Earth is fascinating to many. How can it be? What keeps a satellite up?

See Answer

One might think that an inward force would move a satellite right into the center of the circle; but that's only the case if the satellite were in a rest position. Being that the satellite is already in motion in a tangential direction, the inward force merely turn from its straight-line tangential direction. Instead of turning and falling into the earth, it turns and curves around the earth (thanks to the fact that the earth is round.)

2. If there is an inward force acting upon an earth orbiting satellite, then why doesn't the satellite collide into the Earth?

See Answer

The previous question provides most of the reasoning for this. A combination of a tangential velocity and a curved earth prevents this collision. If it is your belief that the direction an object moves is always in the same direction of the force, then you have a misconception. Lots of objects move in a direction different from a force. For instance as your car heads east and and slam on your brakes, the force on the car is westward; only the acceleration would be westward. And for satellites, the direction of motion is tangential and the force is inward; only the acceleration is inward and this cause the circular motion around the central body.