Kepler's Three Laws
Planetary and Satellite Motion
In the early 1600s, Johannes Kepler proposed three laws of
planetary motion. Kepler was able to summarize the carefully collected data of
his mentor - Tycho Brahe - with three
statements that described the motion of planets in a sun-centered solar
system. Kepler's efforts to explain the underlying reasons for such motions are
no longer accepted; nonetheless, the actual laws themselves are still
considered an accurate description of the motion of any planet and any
satellite.
Kepler's three laws of planetary motion can be described as
follows:
· The path
of the planets about the sun is elliptical in shape, with the center of the sun being located at one focus. (The Law
of Ellipses)
· An
imaginary line drawn from the center of the
sun to the center of the planet will sweep
out equal areas in equal intervals of time. (The Law of Equal Areas)
· The ratio
of the squares of the periods of any two planets is equal to the ratio of the
cubes of their average distances from the sun. (The Law of Harmonies)
The Law of Ellipses
Kepler's first law - sometimes referred to as the law of
ellipses - explains that planets are orbiting the sun in a path described as an
ellipse. An ellipse can easily b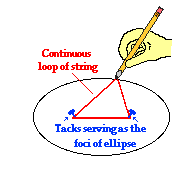e 
constructed using a pencil, two tacks, a string, a sheet of paper and a
piece of cardboard. Tack the sheet of paper to the cardboard using the two
tacks. Then tie the string into a loop and wrap the loop around the two tacks.
Take your pencil and pull the string until the pencil and two tacks make a
triangle (see diagram at the right). Then begin to trace out a path with the
pencil, keeping the string wrapped tightly around the tacks. The resulting
shape will be an ellipse. An ellipse is a special curve in which the sum of the
distances from every point on the curve to two other points is a constant. The
two other points (represented here by the tack locations) are known as the foci of the
ellipse. The closer together that these points are, the more closely that the
ellipse resembles the shape of a circle. In fact, a circle is the special case
of an ellipse in which the two foci are at the same location. Kepler's first
law is rather simple - all planets orbit the sun in a path that resembles an
ellipse, with the sun being located at one of the foci of that ellipse.
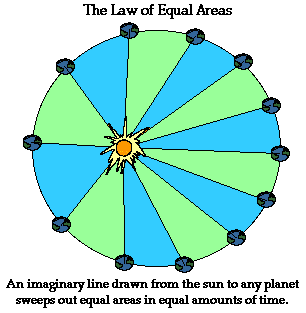
The
Law of Equal Areas
Kepler's second law - sometimes referred to as the law of
equal areas - describes the speed at which any given planet will move while
orbiting the sun. The speed at which any planet moves through space is
constantly changing. A planet moves fastest when it is closest to the sun and
slowest when it is furthest from the sun. Yet, if an imaginary line were drawn
from the center of the planet to the center of the sun, that line would sweep out the same
area in equal periods of time. For instance, if an imaginary line were drawn
from the earth to the sun, then the area swept out by the line in every 31-day
month would be the same. This is depicted in the diagram below. As can be
observed in the diagram, the areas formed when the earth is closest to the sun
can be approximated as a wide but short triangle; whereas the areas formed when
the earth is farthest from the sun can be approximated as a narrow but long
triangle. These areas are the same size. Since the base of these triangles are shortest when
the earth is farthest from the sun, the earth would have to be moving more
slowly in order for this imaginary area to be the same size as when the earth
is closest to the sun.
The
Law of Harmonies
Kepler's third law - sometimes referred to as the law of harmonies - compares
the orbital period and radius of orbit of a planet to those of other planets.
Unlike Kepler's first and second laws that describe the motion characteristics
of a single planet, the third law makes a comparison between the motion
characteristics of different planets. The comparison being made is that the
ratio of the squares of the periods to the cubes of their average distances
from the sun is the same for every one of the planets. As an illustration,
consider the orbital period and average distance from sun (orbital radius) for
Earth and mars as given in the table below.
|
Planet |
Period |
Average |
T2/R3 |
|
Earth |
3.156 x 107 s |
1.4957 x 1011 |
2.977 x 10-19 |
|
Mars |
5.93 x 107 s |
2.278 x 1011 |
2.975 x 10-19 |
Observe that the T2/R3 ratio is the same for Earth as it is for mars. In fact, if the same T2/R3 ratio is
computed for the other planets, it can be found that this ratio is nearly the same value for all the planets (see table below).
Amazingly, every planet has the same T2/R3 ratio.
|
Planet |
Period |
Average |
T2/R3 |
|
Mercury |
0.241 |
0.39 |
0.98 |
|
Venus |
.615 |
0.72 |
1.01 |
|
Earth |
1.00 |
1.00 |
1.00 |
|
Mars |
1.88 |
1.52 |
1.01 |
|
Jupiter |
11.8 |
5.20 |
0.99 |
|
Saturn |
29.5 |
9.54 |
1.00 |
|
Uranus |
84.0 |
19.18 |
1.00 |
|
Neptune |
165 |
30.06 |
1.00 |
|
Pluto |
248 |
39.44 |
1.00 |
(NOTE: The average distance value is given in
astronomical units where 1 a.u. is equal to the
distance from the earth to the sun - 1.4957 x 1011 m. The orbital period is given in
units of earth-years where 1 earth year is the time required for the earth to
orbit the sun - 3.156 x 107 seconds.
)
Kepler's third law provides an accurate description of the
period and distance for a planet's orbits about the sun. Additionally, the same
law that describes the T2/R3 ratio for the planets' orbits about the sun
also accurately describes the T2/R3 ratio for any satellite (whether a moon or a
man-made satellite) about any planet. There is something much deeper to be
found in this T2/R3 ratio - something that must relate to basic
fundamental principles of motion., these principles will be investigated as we
draw a connection between the circular motion principles discussed in Lesson 1
and the motion of a satellite.
How did Newton Extend His Notion of Gravity to
Explain Planetary Motion?
Newton's comparison of the acceleration of the moon to the
acceleration of objects on earth allowed him to establish that the moon is held in a circular orbit by the force of gravity - a force that is inversely dependent upon the distance between
the two objects' centers. Establishing gravity
as the cause of the moon's orbit does not necessarily establish that gravity is
the cause of the planet's orbits. How then did Newton provide credible evidence
that the force of gravity is meets the centripetal force requirement for the
elliptical motion of planets?
that Johannes Kepler
proposed three laws of planetary motion. His Law of Harmonies suggested that
the ratio of the period of orbit squared (T2) to the mean radius of orbit cubed (R3) is the same value k for all the planets that orbit the sun. Known data for the
orbiting planets suggested the following average ratio:
k = 2.97 x 10-19 s2/m3 =
(T2)/(R3)
Newton was able to combine the law of universal gravitation
with circular motion principles to show that if the force of gravity provides
the centripetal force for the planets' nearly circular orbits, then a value
of 2.97 x 10-19 s2/m3 could be predicted for the T2/R3 ratio. Here is the reasoning employed by Newton:
Consider a planet with mass Mplanet to
orbit in nearly circular motion about the sun of mass MSun.
The net centripetal force acting upon this orbiting planet is given by the
relationship
Fnet = (Mplanet * v2) / R
This net centripetal force is the result of the gravitational
force that attracts the planet towards the sun, and can be represented as
Fgrav =
(G* Mplanet * MSun ) / R2
Since Fgrav = Fnet, the above expressions for centripetal
force and gravitational force are equal. Thus,
(Mplanet *
v2) / R = (G* Mplanet * MSun ) / R2
Since the velocity of an object in nearly circular orbit can
be approximated as v = (2*pi*R) / T,
v2 = (4 * pi2 *
R2) / T2
Substitution of the expression for v2 into
the equation above yields,
(Mplanet *
4 * pi2 * R2) / (R • T2) = (G* Mplanet * MSun ) / R2
By cross-multiplication and simplification, the equation can
be transformed into
T2 / R3 =
(Mplanet * 4 * pi2) /
(G* Mplanet * MSun )
The mass of the planet can then be canceled from
the numerator and the denominator of the equation's right-side, yielding
T2 / R3 =
(4 * pi2) / (G * MSun )
The right side of the above equation will be the same value
for every planet regardless of the planet's mass.
Subsequently, it is reasonable that the T2/R3 ratio would be the same value for all planets if the force that
holds the planets in their orbits is the force of gravity. Newton's universal
law of gravitation predicts results that were consistent with known planetary
data and provided a theoretical explanation for Kepler's Law of Harmonies.
Check Your Understanding
1. Our understanding of the elliptical motion of planets
about the Sun spanned several years and included contributions from many
scientists.
a. Which scientist is credited with the collection of the
data necessary to support the planet's elliptical motion?
b. Which scientist is credited with the long and difficult
task of analyzing the data?
c. Which scientist is credited with the accurate explanation
of the data?
Tycho Brahe gathered the
data. Johannes Kepler analyzed the data.
Isaac Newton explained the data - and that's what the next part of Lesson 4 is
all about.
close
2. Galileo is often credited with the early discovery of four
of Jupiter's many moons. The moons orbiting Jupiter follow the same laws of
motion as the planets orbiting the sun. One of the moons is called Io - its
distance from Jupiter's center is 4.2 units and it orbits Jupiter in 1.8
Earth-days. Another moon is called Ganymede; it is 10.7 units from
Jupiter's center. Make a prediction of the
period of Ganymede using Kepler's law of harmonies.
Answer: T = 7.32 days
Given:
Io: Rio = 4.2 and Tio =
1.8
Ganymede: Rg =
10.7 Tg=???
Use Kepler's 3rd law to solve.
(Tio)^2/(Rio)3 =
0.04373;
so (Tg)^2
/ (Rg)3 = 0.04373
Proper algebra would yield (Tg)^2 = 0.04373 • (Rg)3
(Tg)2 =
53.57 so Tg = SQRT(53.57) = 7.32
days
3. Suppose a small planet is discovered that is 14 times as
far from the sun as the Earth's distance is from the sun (1.5 x 1011 m). Use Kepler's law of harmonies to
predict the orbital period of such a planet. GIVEN: T2/R3 = 2.97 x 10-19 s2/m3
Answer: T = 7.32 days
Given:
Io: Rio = 4.2 and Tio =
1.8
Ganymede: Rg =
10.7 Tg=???
Use Kepler's 3rd law to solve.
(Tio)^2/(Rio)3 =
0.04373;
so (Tg)^2
/ (Rg)3 = 0.04373
Proper algebra would yield (Tg)^2 = 0.04373 • (Rg)3
(Tg)2 =
53.57 so Tg = SQRT(53.57) = 7.32
days
4. The average orbital distance of Mars is 1.52 times the
average orbital distance of the Earth. Knowing that the Earth orbits the sun in
approximately 365 days, use Kepler's law of harmonies to predict the time for
Mars to orbit the sun.
Given: Rmars =
1.52 • Rearth and Tearth = 365 days
Use Kepler's third law to relate the ratio of the period squared
to the ratio of radius cubed
(Tmars)2 /
(Tearth)2 • (Rmars)3 / (Rearth)3
(Tmars)2 =
(Tearth)2 • (Rmars)3 / (Rearth)3
(Tmars)2 =
(365 days)2 * (1.52)3
(Note the Rmars / Rearth ratio is 1.52)
Tmars = 684 days
Orbital radius and orbital period data for the four biggest
moons of Jupiter are listed in the table below. The mass of the planet Jupiter
is 1.9 x 1027 kg. Base
your answers to the next five questions on this information.
|
Jupiter's Moon |
Period (s) |
Radius (m) |
T2/R3 |
|
Io |
1.53 x 105 |
4.2 x 108 |
a. |
|
Europa |
3.07 x 105 |
6.7 x 108 |
b. |
|
Ganymede |
6.18 x 105 |
1.1 x 109 |
c. |
|
Callisto |
1.44 x 106 |
1.9 x 109 |
d. |
5. Determine the T2/R3 ratio
(last column) for Jupiter's moons.
a. (T2) / (R3) = 3.16 x 10-16 s2/m3
b. (T2) / (R3) = 3.13 x 10-16 s2/m3
c. (T2) / (R3) = 2.87 x 10-16 s2/m3
d. (T2)
/ (R3) = 3.03 x 10-16 s2/m3
6. What pattern do you observe in the last column of data?
Which law of Kepler's does this seem to support?
The
(T2) / (R3) ratios are approximately the same for each of
Jupiter's moons. This is what would be predicted by Kepler's third law!
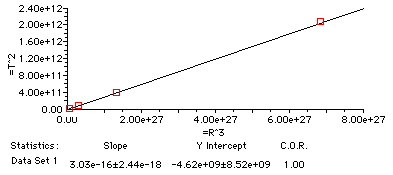
7. Use the graphing capabilities of your TI calculator to
plot T2 vs. R3 (T2 should be plotted along the vertical
axis) and to determine the equation of the line. Write the equation in
slope-intercept form below.
See graph below.
T2 = (3.03 * 10-16) * R3 -
4.62 * 10+9
Given the uncertainty in the y-intercept value, it can be
approximated as 0.
Thus, T2 =
(3.03 * 10-16) * R3
8. How does the T2/R3 ratio for Jupiter (as shown in the last column
of the data table) compare to theT2/R3 ratio
found in #7 (i.e., the slope of the line)?
The values are
almost the same - approximately 3 x 10-16.
close
9. How does the T2/R3 ratio for Jupiter (as shown in the last column
of the data table) compare to theT2/R3 ratio
found using the following equation? (G=6.67x10-11 N*m2/kg2 and MJupiter = 1.9 x 1027 kg)
T2 /
R3 = (4 * pi2)
/ (G * MJupiter )
The values in
the data table are approx. 3 x 10-16. The value of 4*pi/(G*MJupiter) is
approx. 3.1 x 10-16.
