Cavendish and the Value of G

Isaac Newton's law of universal gravitation proposed that the gravitational attraction between any two objects is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centers. In equation form, this is often expressed as follows:

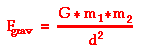
The constant of proportionality in this equation is G - the universal gravitation constant. The value of G was not experimentally determined until nearly a century later (1798) by Lord Henry Cavendish using a torsion balance.

Cavendish's apparatus for experimentally determining the value of G involved a light, rigid rod about 2-feet long. Two small lead spheres were attached to the ends of the rod and the rod was suspended by a thin wire. When the rod becomes twisted, the torsion of the wire begins to exert a torsional force that is proportional to the angle of rotation of the rod. The more twist of the wire, the more the system pushesbackwards to restore itself towards the original position. Cavendish had calibrated his instrument to determine the relationship between the angle of rotation and the amount of torsional force. A diagram of the apparatus is shown below.

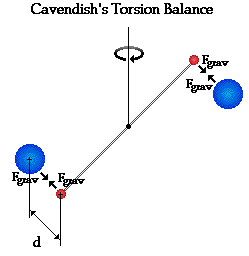
Cavendish then brought two large lead spheres near the smaller spheres attached to the rod. Since all masses attract, the large spheres exerted a gravitational force upon the smaller spheres and twisted the rod a measurable amount. Once the torsional force balanced the gravitational force, the rod and spheres came to rest and Cavendish was able to determine the gravitational force of attraction between the masses. By measuring m₁, m₂, d and F_grav, the value of G could be determined. Cavendish's measurements resulted in an experimentally determined value of 6.75 x 10^-11 N m²/kg². Today, the currently accepted value is 6.67259 x 10^-11 N m²/kg².

The value of G is an extremely small numerical value. Its smallness accounts for the fact that the force of gravitational attraction is only appreciable for objects with large mass. While two students will indeed exert gravitational forces upon each other, these forces are too small to be noticeable. Yet if one of the students is replaced with a planet, then the gravitational force between the other student and the planet becomes noticeable.

Check Your Understanding

Suppose that you have a mass of 70 kg (equivalent to a 154-pound person). How much mass must another object have in order for your body and the other object to attract each other with a force of 1-Newton when separated by 10 meters?

See Answer

m = 2.14 x 10¹⁰ kg                                                 

Use the equation F_grav = G • m₁ • m₂ / d²

where m₁ = 70 kg, d = 10 m and G = 6.673 x 10^-11 N•m²/kg².

Substitute and solve for m₂.

Note that the object is equivalent to an approximately 23 million ton object!! It takes a large mass to have a significant gravitational force.