The Apple, the Moon, and the Inverse Square Law
In the early 1600's, German mathematician and astronomer
Johannes Kepler mathematically analyzed known astronomical data in order to
develop three laws to describe the motion of planets about the sun. Kepler's
three laws emerged from the analysis of data carefully collected over a span of
several years by his Danish predecessor and teacher, Tycho Brahe. Kepler's three laws
of planetary motion can be briefly described as follows:
· The paths
of the planets about the sun are elliptical in shape, with the center of the sun being located at one focus. (The Law
of Ellipses)
· An
imaginary line drawn from the center of the
sun to the center of the planet will sweep
out equal areas in equal intervals of time. (The Law of Equal Areas)
· The ratio
of the squares of the periods of any two planets is equal to the ratio of the
cubes of their average distances from the sun. (The Law of Harmonies)
While Kepler's laws provided a suitable framework for
describing the motion and paths of planets about the sun, there was no accepted
explanation for why such paths existed. The cause for how the planets moved as
they did was never stated. Kepler could only suggest that there was some sort
of interaction between the sun and the planets that provided the driving force
for the planet's motion. To Kepler, the planets were somehow "magnetically"
driven by the sun to orbit in their elliptical trajectories. There was however
no interaction between the planets themselves.
Newton was troubled by the lack of explanation for the
planet's orbits. To Newton, there must be some cause for such elliptical
motion. Even more troubling was the circular motion of the moon about the
earth. Newton knew that there must be some sort of force that governed the
heavens; for the motion of the moon in a circular path and of the planets in an
elliptical path required that there be an inward component of force. Circular
and elliptical 
motion were clearly departures from the inertial paths (straight-line)
of objects. And as such, these celestial motions required a cause in the form
of an unbalanced force. As learned in Lesson 1, circular motion (as well as
elliptical motion) requires a centripetal force. The nature of such a force -
its cause and its origin - bothered Newton for some time and was the fuel for
much mental pondering. And according to legend, a breakthrough came at age 24
in an apple orchard in England. Newton never wrote of such an event, yet it is
often claimed that the notion of gravity as the cause of all heavenly motion
was instigated when he was struck in the head by an apple while lying under a
tree in an orchard in England. Whether it is a myth or a reality, the fact is
certain that it was Newton's ability to relate the cause for heavenly motion
(the orbit of the moon about the earth) to the cause for Earthly motion (the
falling of an apple to the Earth) that led him to his notion of universal gravitation.
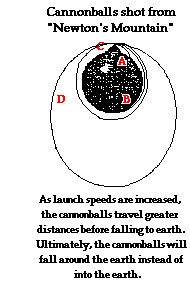Newton's
Mountain Thought Experiment
A survey of Newton's writings reveals an illustration similar
to the one shown at the right. The illustration was accompanied by an extensive
discussion of the motion of the moon as a projectile. Newton's reasoning
proceeded as follows. Suppose a cannonball is fired horizontally from a very
high mountain in a region devoid of air resistance. In the absence of gravity,
the cannonball would travel in a straight-line, tangential path. Yet in the
presence of gravity, the cannonball would drop below this straight-line path
and eventually fall to Earth (as in path A). Now suppose that the cannonball is fired
horizontally again, yet with a greater speed. In this case, the cannonball
would still fall below its straight-line tangential path and eventually drop to
earth. Only this time, the cannonball would travel further before striking the
ground (as in path B). Now suppose that there is a speed at which
the cannonball could be fired such that the trajectory of the falling
cannonball matched the curvature of the earth. If such a speed could be
obtained, then the cannonball would fall around the earth instead of into it.
The cannonball would fall towards the Earth without ever colliding into it and
subsequently become a satellite orbiting in circular motion (as in path C). And then at even greater launch speeds, a cannonball would once more
orbit the earth, but in an elliptical path (as in path D). The motion of the cannonball orbiting to the earth under the
influence of gravity is analogous to the motion of the moon orbiting the Earth.
And if the orbiting moon can be compared to the falling cannonball, it can even
be compared to a falling apple. The same force that causes objects on Earth to
fall to the earth also causes objects in the heavens to move along their circular
and elliptical paths. Quite amazingly, the laws of mechanics that govern the
motions of objects on Earth also govern the movement of objects in the heavens.
Newton's Argument for Gravity Being Universal
Of course, Newton's dilemma was to provide reasonable
evidence for the extension of the force of gravity from earth to the heavens.
The key to this extension demanded that he be able to show how the affect of
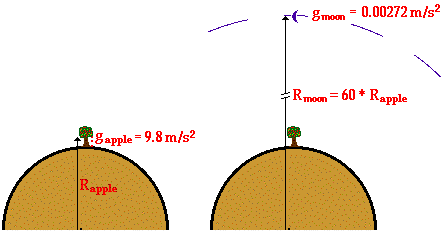
gravity is diluted with distance. It was known at the time, that the force of
gravity causes earthbound objects (such as falling apples) to accelerate
towards the earth at a rate of 9.8 m/s2. And it was also known that
the moon accelerated towards the earth at a rate of 0.00272 m/s2. If
the same force that causes the acceleration of the apple to the earth also
causes the acceleration of the moon towards the earth, then there must be a
plausible explanation for why the acceleration of the moon is so much smaller
than the acceleration of the apple. What is it about the force of gravity that
causes the more distant moon to accelerate at a rate of acceleration that is
approximately 1/3600-th the acceleration of the apple?
Newton knew that the force of gravity must somehow be
"diluted" by distance. But how? What mathematical reality is
intrinsic to the force of gravity that causes it to be inversely dependent upon
the distance between the objects?
The riddle is solved by a comparison of the distance from the
apple to the center of the earth with the distance from the moon to the center of
the earth. The moon in its orbit about the earth is approximately 60 times
further from the earth's center than the apple is. The mathematical relationship becomes clear.
The force of gravity between the earth and any object is inversely proportional
to the square of the distance that separates that object from the earth's center. The
moon, being 60 times further away than the apple, experiences a force of
gravity that is 1/(60)2 times that
of the apple. The force of gravity follows an inverse square law.
The relationship between the force of gravity (Fgrav) between the earth and any other object and the distance that separates
their centers (d) can be
expressed by the following relationship
Since the distance d is in the denominator of this
relationship, it can be said that the force of gravity is inversely related to
the distance. And since the distance is raised to the second power, it can be
said that the force of gravity is inversely related to the square of the
distance. This mathematical relationship is sometimes referred to as an inverse
square law since one quantity depends inversely upon the square of the other quantity.
The inverse square relation between the force of gravity and the distance of
separation provided sufficient evidence for Newton's explanation of why gravity
can be credited as the cause of both the falling apple's acceleration and the
orbiting moon's acceleration.
Using
Equations as a Guide to Thinking
The inverse square law proposed by Newton suggests that the
force of gravity acting between any two objects is inversely proportional to
the square of the separation distance between the object's centers. Altering
the separation distance (d) results in an alteration in the force of gravity
acting between the objects. Since the two quantities are inversely
proportional, an increase in one quantity results in a decrease in the value of
the other quantity. That is, an increase in the separation distance causes a
decrease in the force of gravity and a decrease in the separation distance
causes an increase in the force of gravity. Furthermore, the factor by
which the force of gravity is changed is the square of the factor by which the
separation distance is changed. So if the separation distance is doubled
(increased by a factor of 2), then the force of gravity is decreased by a
factor of four (2 raised to the second power). And if the separation distance
is tripled (increased by a factor of 3), then the force of gravity is decreased
by a factor of nine (3 raised to the second power). Thinking of the
force-distance relationship in this way involves using a mathematical
relationship as a guide to thinking about how an alteration in one variable
affects the other variable. Equations can be more than recipes for algebraic
problem solving; they can be guides
to thinking. Check your understanding of the inverse square law as a guide
to thinking by answering the following questions below. When finished, click
the button to check your answers.
Check Your Understanding
1 . Suppose
that two objects attract each other with a gravitational force of 16 units. If
the distance between the two objects is doubled, what is the new force of
attraction between the two objects?
Answer: F = 4 units
If the distance is increased by a factor of 2, then force will
be decreased by a factor of 4 (22). The new force is then 1/4 of the
original 16 units.
F = (16 N) / 4 =
4 units
2. Suppose that two objects attract each other with a
gravitational force of 16 units. If the distance between the two objects is
tripled, then what is the new force of attraction between the two objects?
Answer: F = 1.78 units
If the distance is increased by a factor of 3, then force will
be decreased by a factor of 9 (32). The new force is then 1/9 of the
original 16 units.
F = (16 N) / 9 =
1.78 units
3. Suppose that two objects attract each other with a
gravitational force of 16 units. If the distance between the two objects is
reduced in half, then what is the new force of attraction between the two
objects?
Answer: F = 400 units
If the distance is decreased by a factor of 5, then force will
be increased by a factor of 25 (52). The new force is then 25 times
the original 16 units.
F = (16 N) • 25
= 400 units
4. Suppose that two objects attract each other with a
gravitational force of 16 units. If the distance between the two objects is
reduced by a factor of 5, then what is the new force of attraction between the
two objects?
Answer: F = 400 units
If the distance is decreased by a factor of 5, then force will
be increased by a factor of 25 (52). The new force is then 25 times
the original 16 units.
F = (16 N) • 25
= 400 units
5. Having recently completed his first Physics course, Noah
Formula has devised a new business plan based on his teacher's Physics for Better Living theme. Noah learned that objects
weigh different amounts at different distances from Earth's center. His plan
involves buying gold by the weight at one altitude and then selling it at
another altitude at the same price per weight. Should Noah buy at a high
altitude and sell at a low altitude or vice versa?
To profit, buy at a high altitude and sell at a low one.
Gold will weigh
less at a high altitude and so you will get more gold for your money by buying
at the high altitude. Then sell at a low altitude where the gold will weigh
more than it did where it was purchased. This illustrates the inverse
relationship between force of gravity (a.k.a. "weight") and distance
from Earth's center.