Athletics

Circular motion is common to almost all sporting events. Whether it is sports car racing or track and field, baseball running or ice-skating, the motion of objects in circles is a common observation of sports viewers around the world. Like any object moving in a circle, the motion of these objects that we view from the stadium bleachers or watch upon the television monitor are governed by Newton's laws of motion. Their circular motion - however brief or prolonged they may be - is characterized by an inward acceleration and caused by an inward net force. The mathematical analysis of such motions can be conducted in the manner presented old topics. In this topic we will investigate a variety of applications of circular motion principles to the world of sports and use Newton's laws to mathematically analyze such motions. The emphasis will not be upon an investigation of the details of every possible sport, but rather upon learning how to apply some general principles so that they can subsequently be applied to every sport.

Making the Turn

The most common example of the physics of circular motion in sports involves the turn. It could be a halfback in football making a turn around the corner of the line. Or it could be a softball player running the bases and making a turn around second base. Or it could be a bobsled in the Olympic games making a turn around a corner on the track. Whatever turning motion it happens to be, you can be sure that turning a corner involves circular motion principles. Now for certain not all turns involve a complete circle; nor do all turns have a perfectly circular shape. Some turns are only one-quarter of a turn - such as the fullback rounding the corner of the line in football. And some turns are hardly circular whatsoever. Nonetheless, any turn can be approximated as being a part of a larger circle or a part of several circles of varying size. A sharp turn can be considered part of a small circle. A more gradual turn is part of a larger circle. Some turns can begin sharply and gradually change in sharpness, or vice versa. In all cases, the motion around a turn can be approximated as part of a circle or a collection of circles. The diagram below depicts a variety of paths that a turn could make.

Because turning a corner involves the motion of an object that is momentarily moving along the path of a circle, both the concepts and the mathematics of circular motion can be applied to such a motion. Conceptually, such an object is moving with an inward acceleration - the inward direction being towards the center of whatever circle the object is moving along. There would also be a centripetal force requirement for such a motion. That is, there must be some object supplying an inward force or inward component of force. When a person makes a turn on a horizontal surface, the person often leans into the turn. By leaning, the surface pushes upward at an angle to the vertical. As such, there is both a horizontal and a vertical component resulting from contact with the surface below. This contact force supplies two roles - it balances the downward force of gravity and meets the centripetal force requirement for an object in uniform circular motion. The upward component of the contact force is sufficient to balance the downward force of gravity and the horizontal component of the contact force pushes the person towards the center of the circle. This contact force is depicted in the diagram below for a speed skater making a turn on ice.

In the case of the speed skater above, the force resulting from the contact between ice skates and ice has two components to it. The force is a vector combination of a normal force and a friction force. The normal force is the result of the stable surface providing support for any object pushing downward against it. The friction force is the result of the static friction force resulting from the ice-skate interaction. As the skater leans into the turn, she pushes downward and outward upon the ice. The high pressure and temperature of the blade upon the ice creates a shallow groove in which the blade momentarily rests. The blade pushes outward upon the vertical wall of this groove and downward upon the floor of this groove. As we would expect from Newton's third law of motion, there is a reaction force of the ice pushing upward and inward upon the skate. If this blade-ice action does not occur, the skater could still lean and still try to push outward upon the ice. However, the blade would not get a grip upon the ice and the skater would be at risk of not making the turn. As a result, the ice skater's skates would move out from under her, she would fall to the ice, and she would travel in a straight-line inertial path. Without an inward force, the skater cannot travel through the turn.

The same principle of lean that allows the speed skater to make the turn around a portion of the circle applies to the wealth of other sporting events where participants lean into the turn in order to momentarily move in a circle. A downhill skier makes her turn by leaning into the snow. The snow pushes back in both an inward and an upward direction - balancing the force of gravity and supplying the centripetal force. A football player makes his turn by leaning into the ground. The ground pushes back in both an inward and upward direction - balancing the force of gravity and supplying both the centripetal force. A cyclist makes his turn in a similar manner as he leans at an angle to the horizontal. The road surface pushes with an upward component of force to balance the downward force of gravity. The road surface also pushes with a horizontal component of force towards the center of the circle through which the cyclist is turning. A bobsled team makes their turn in a similar manner as they rise up onto the inclined section of track. Upon the incline, they naturally lean and the normal force acts at an angle to the vertical; this normal force supplies both the upward force to balance the force of gravity and the centripetal force to allow for the circular motion.

A turn is only possible when there is a component of force directed towards the center of the circle about which the person is moving.

Force Analysis of Turns in Athletics

The same mathematical equations that describe the motion of objects in circles apply to the motion of athletes making turns on the athletic field. The use of these circular motion equations were introduced in the first section of Lesson 1 and then subsequently applied to the analysis of the motion of roller coaster cars. It has been emphasized that any given physical situation can be analyzed in terms of the individual forces that are acting upon an object; these individual forces must add up to the net force. Furthermore, the net force must be equal to the mass times the acceleration. The process of conducting a force analysis of a physical situation Now we will investigate the use of these fundamental principles in the analysis of situations involving the motion of athletes in circles. We will utilize the basic problem-solving approach that was introduced earlier in Lesson 2. This approach can be summarized as follows.

Suggested Method of Solving Circular Motion Problems

1. From the verbal description of the physical situation, construct a free-body diagram. Represent each force by a vector arrow and label the forces according to type.

2. Identify the given and the unknown information (express in terms of variables such as m= ,a= , v= , etc.).

3. If any of the individual forces are directed at angles to the horizontal and the vertical, then use vector principles to resolve such forces into horizontal and vertical components.

4. Determine the magnitude of any known forces and label on the free-body diagram.
(For example, if the mass is given, then the F_grav can be determined. And as another example, if there is no vertical acceleration, then it is known that the vertical forces or force components balance, allowing for the possible determination of one or more of the individual forces in the vertical direction.)

5. Use circular motion equations to determine any unknown information.
(For example, if the speed and the radius are known, then the acceleration can be determined. And as another example, if the period and radius are known, then the acceleration can be determined.)

6. Use the remaining information to solve for the requested information.

a. If the problem requests the value of an individual force, then use the kinematic information (R, T and v) to determine the acceleration and the F_net ; then use the free-body diagram to solve for the individual force value.

b. If the problem requests the value of the speed or radius, then use the values of the individual forces to determine the net force and acceleration; then use the acceleration to determine the value of the speed or radius.

Combine a force analysis with the above method to solve the following circular motion problem.

Sample Speed Skater Problem

Bonnie is ice-skating at the Olympic games. She is making a sharp turn with a radius of 22.6 m and with a speed of 16.1 m/s. Use Newton's second law to determine the acceleration and the angle of lean of Bonnie's 55.0-kg body.

Steps 1 and 2 involve the construction of a free body diagram and the identification of known and unknown quantities. This is shown in below.

Given Info: m = 55.0 kg v = 16.1 m/s r = 22.6 m Find: a = ??? Angle of lean = ???

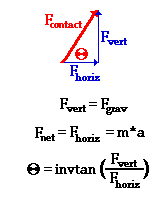Step 3 of the suggested method involves resolving any forces that act at angles into horizontal and vertical components. This is shown in the diagram at the right. The contact force can be broken into two components - F_horiz and F_vert. The vertical component of force would balance the force of gravity; and as such, the vertical component will be equal in magnitude to the force of gravity. The horizontal component of force remains unbalanced. As mentioned in the above discussion, this horizontal component is the net inward force; and as such, F_horiz is equal to m*a. Finally, the two components are related to the angle of lean by the tangent function. Simple algebraic manipulation would yield the relationship shown in the graphic at the right. So the angle of lean can be found if the vertical and horizontal components of force are known.

Step 4 of the suggested method involves the determination of any known forces. In this case, the force of gravity can be determined from the equation F_grav = m • g. o the force of gravity acting upon Bonnie's 55.0-kg body is approximately 539 N. And since this force is balanced by the vertical component of the contact force, the F_vert is also 539 N. Step 5 involves determination of Bonnie's acceleration as she makes the turn. This can be accomplished by using the acceleration equation for circular motion.

a = v²/R

a = (16.1 m/s)²/(22.6 m) = 11.5 m/s²

Now that the acceleration has been found, the angle of lean can be determined. As mentioned in the equation above, the angle of lean ("theta") can be determined from knowledge of the horizontal and vertical components of the contact force. The vertical component has already been calculated to be 539 N (equal to F_grav). And as previously mentioned, the horizontal component would be equal to F_net; this is shown below.

F_horiz = F_net = m•a

F_horiz = (55.0 kg)•(11.5 m/s/s) = 631 N

Now finally the angle of lean can be determined.

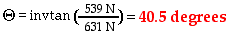
The above problem illustrates the procedure of combining Newton's second law of motion with vector principles and circular motion equations in order to analyze turning motions of athletes. Now utilize the same general procedure described above to solve the following practice problem. When finished, click the button to view the answers.

Circular Motion in Football

A 90-kg GBS fullback is running a sweep around the left side of the line. The fullback's path as seen from above is shown in the diagram. As he rounds the turn, he is momentarily moving in circular motion, sweeping out a quarter-circle with a radius of 4.0 meters. The fullback makes the turn with a speed of 5.0 m/s. Use a free-body diagram and your understanding of circular motion and Newton's second law to determine

a. acceleration
b. F_grav
c. F_norm
d. F_frict
e. Angle of lean

See Answer

a = v² / R =(5.0 m/s)² / (4.0 m) = 6.25 m/s/s

F_net = m•a = (90.0 kg)•(6.25 m/s/s) = 563 N

F_grav = F_vert = m•g = 882 N (using g = 9.8 m/s/s)

F_horiz = F_net = 563 N

Theta = invtan(F_vert / F_horiz ) = invtan(882 N / 563 N)

Theta = 57 degrees

Turning motions are not the only situations in sports in which people or objects move in circles. While turning motions are probably the most common examples of circular motion, they are not the only examples. There are certain track and field events - the hammer throw and the discus - in which athletes gather momentum in an object that is to be subsequently thrown. The pre-throw momentum is imparted to the projectile by whirling within a circle. Once momentum has been accumulated, the hammer or discus is launched into the air at an optimum angle in order to maximize the distance it travels. Regardless of the athletic event, the analysis of the circular motion remains the same. Newton's laws describe the force-mass-acceleration relationship; vector principles describe the relationship between individual forces and any angular forces; and circular motion equations describe the speed-radius-acceleration relationship.

Check Your Understanding

1. A 55.0-kg softball player runs at 7.0 m/s around a curve whose radius is 15.0 m. The contact force (vector combination of the frictional force and the normal force) acting between the ground and the player's feet supply both the centripetal force for making the turn and the upward force for balancing the player's weight. Use a free-body diagram and your understanding of circular motion and Newton's second law to determine:

a. acceleration

b. F_grav

c. F_norm

d. F_frict

e. Angle of lean

See Answer

a = v² / R = (7.0 m/s)² / (15.0 m) = 3.27 m/s/s

F_net = m • a = (55.0 kg) • (3.27 m/s/s) = 180 N

F_grav = F_vert = m • g = 539 N

F_horiz = F_net = F_frict = 180 N

Theta = invtan(F_vert / F_horiz) = invtan( 539 N / 180 N )

Theta = 71.6 degrees

2. In the hammer throw, a sphere is whirled around in a circular path on the end of a chain. After revolving about five times the thrower releases his grip on the chain and the "hammer" is launched at an angle to the horizontal. A diagram of the athlete and the hammer is shown to the right. Assume that the hammer is moving in a circle in a horizontal plane with a speed of 27.0 m/s. Assume that the hammer has a mass of 7.30-kg and that it moves in a circle with a 1.25-m radius. Since the hammer is moving in a horizontal plane, the centripetal force is directed horizontally. The vertical component of the tension in the chain (directed upward) is balanced by the weight of the hammer (directed downward). Use the diagram and an understanding of vector components to determine the tension in the chain.

See Answer

a = v² / R = (27.0 m/s)² / (1.25 m) = 583 m/s/s

F_net = m • a = (7.30 kg) • (583 m/s/s) = 4257 N

F_grav = F_vert = m • g = 71.5 N

F_horiz = F_net = 4257 N

F_tens = SQRT(F_vert² + F_horiz²)

F_tens = 4258 N