Newton's Second Law – Revisited
Applications
of Circular Motion
Newton's second law states that the acceleration of an object is
directly proportional to the net force acting upon the object and inversely
proportional to the mass of the object. The law is often expressed in the form
of the following two equations.
Newton's
Second Law and a Force Analysis
Newton's second law was used to analyze a
variety of physical situations. The idea was that if any given physical
situation is analyzed in terms of the
individual forces that are acting upon an object, then those individual forces
must add up as vectors to the net force. Furthermore, the net force must be
equal to the mass times the acceleration. Subsequently, the acceleration of an
object can be found if the mass of the object and the magnitudes and directions
of each individual force are known. And the magnitude of any individual force
can be determined if the mass of the object, the acceleration of the object,
and the magnitude of the other individual forces are known. The process
of analyzing such physical situations in
order to determine unknown information is dependent upon the ability to
represent the physical situation by means of a free-body diagram. A free-body
diagram is a vector diagram that depicts the relative magnitude and direction
of all the individual forces that are acting upon the object.
Circular Motion in a Horizontal Plane
To illustrate how circular motion
principles can be combined with Newton's second law to analyze a physical situation, consider a car moving in
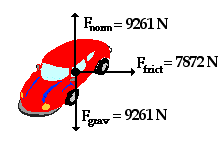
a horizontal circle on a level surface. The diagram below depicts the car on
the left side of the circle.
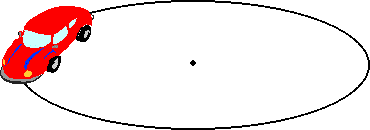
Applying the concept of a centripetal force requirement, we
know that the net force acting upon the object is directed inwards. Since the
car is positioned on the left side of the circle, the net force is directed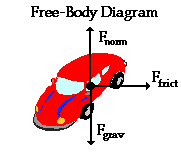
rightward. An analysis of the situation would reveal that there
are three forces acting upon the object - the force of gravity (acting
downwards), the normal force of the pavement (acting upwards), and the force of
friction (acting inwards or rightwards). It is the friction force that supplies
the centripetal force requirement for the car to move in a horizontal circle.
Without friction, the car would turn its wheels but would not move in a circle
(as is the case on an icy surface). This analysis leads to the free-body
diagram shown at the right. Observe that each force is represented by a vector
arrow that points in the specific direction that the force acts; also notice
that each force is labeled according to
type (Ffrict, Fnorm,
and Fgrav). Such an analysis is the
first step of any problem involving Newton's second law and a circular motion.
Now consider the following two problems pertaining to this
physical scenario of the car making a turn on a horizontal surface.
|
The
maximum speed with which a 945-kg car makes a 180-degree turn is 10.0 m/s.
The radius of the circle through which the car is turning is 25.0 m.
Determine the force of friction and the coefficient of friction acting upon
the car. Sample Problem #2 The
coefficient of friction acting upon a 945-kg car is 0.850. The car is making
a 180-degree turn around a curve with a radius of 35.0 m. Determine the
maximum speed with which the car can make the turn. |
Sample problem #1 provides
kinematic information (v and R) and requests the value of an individual force.
As such the solution of the problem will demand that the acceleration and the
net force first be determined; then the individual force value can be found by
use of the free-body diagram. Sample problem #2 provides
information about the individual force values (or at least information that
allows for the determination of the individual force values) and requests the
value of the maximum speed of the car. As such, its solution will demand that
individual force values be used to determine the net force and acceleration;
then the acceleration can be used to determine the maximum speed of the car.
The two problems will be solved using the same general principles. Yet because
the given and requested information is different in each, the solution method
will be slightly different.
Solution to Sample Problem #1
The known information and requested information in sample
problem #1 is:
|
Known Information: m
= 945 kg v = 10.0
m/s R = 25.0 m |
Requested Information: Ffrict = ??? μ = ???? (μ -
coefficient of friction) |
The mass of the object can be used to determine the force of
gravity acting in the downward direction. Use the equation
Fgrav = m * g
where g is 9.8
m/s/s. Knowing that there is no vertical acceleration of the car, it can be
concluded that the vertical forces balance each other. Thus, Fgrav = Fnorm=
9261 N. This allows us to determine two of the three
forces identified in the free-body diagram. Only the friction force remains
unknown.
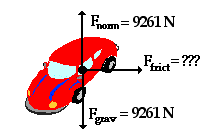
Since the force of friction is the only horizontal force, it
must be equal to the net force acting upon the object. So if the net force can
be determined, then the friction force is known. To determine the net force,
the mass and the kinematic information (speed and radius) must be substituted
into the following equation:
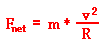
Substituting the given values yields a net force of 3780
Newton. Thus, the force of friction is 3780 N.
Finally the coefficient of friction (μ) can be
determined using the equation that relates the coefficient of friction to the
force of friction and the normal force.
Substituting 3780 N for Ffrict and 9261 N for Fnorm yields a coefficient of friction of 0.408.
Solution to Sample Problem #2
Once again, the problem begins by identifying the known and
requested information. The known information and requested information in the sample
problem #2 is:
|
Known Information: m
= 945 kg μ =
0.85 (coefficient of friction) R = 35.0 m |
Requested Information: v = ??? (the
minimum speed would be the speed achieved with the given friction coefficient) |
The mass of the car can be used to determine the force of
gravity acting in the downward direction. Use the equation
Fgrav = m * g
where g is 9.8
m/s/s. Knowing that there is no vertical acceleration of the car, it can be
concluded that the vertical forces balance each other. Thus, Fgrav = Fnorm=
9261 N. Since the coefficient of friction (μ) is
given, the force of friction can be determined using the following equation:
This allows us to determine all three forces identified in
the free-body diagram.
The net force acting upon any object is the vector sum of all
individual forces acting upon that object. So if all individual force values
are known (as is the case here), the net force can be calculated. The vertical
forces add to 0 N. Since the force of friction is the only horizontal force, it
must be equal to the net force acting upon the object. Thus, Fnet = 7872 N.
Once the net force is determined, the acceleration can be
quickly calculated using the following equation.
Fnet = m*a
Substituting the given values yields an acceleration of 8.33 m/s/s. Finally, the speed at which the car could travel around the turn can
be calculated using the equation for centripetal acceleration:
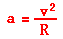
Substituting the known values for a and R into this equation and solving algebraically
yields a maximum speed of 17.1 m/s.
Developing the Proper Problem-Solving Approach
Each of the two sample problems above was solved using the
same basic problem-solving approach. The approach can be summarized as follows.
|
Suggested Method of Solving
Circular Motion Problems 1. From the verbal description of the
physical situation, construct a free-body diagram. Represent each force by a
vector arrow and label the forces according to type. 2. Identify the given and the unknown
information (express in terms of variables such as m= ,a= , v= ,
etc.). 3. If any of the individual forces are
directed at angles to the horizontal and vertical, then usevector principles to resolve such forces into
horizontal and vertical components. 4. Determine the magnitude of any known
forces and label on the free-body diagram. 5. Use circular motion equations to
determine any unknown information. 6. Use the remaining information to solve
for the requested information. · If the problem requests the value of an
individual force, then use the kinematic information (R, T and v) to
determine the acceleration and the Fnet ; then
use the free-body diagram to solve for the individual force value. · If the problem requests the value of
the speed or radius, then use the values of the individual forces to
determine the net force and acceleration; then use the acceleration to
determine the value of the speed or radius. |
The method prescribed above will serve you well as you
approach circular motion problems. However, one caution is in order. Every
physics problem differs from the previous problem. As such, there is no magic formula for solving every one. Using an appropriate approach to
solving such problems (which involves constructing a FBD, identifying known
information, identifying the requested information, and using available
equations) will never eliminate the need to think, analyze and
problem-solve. For this reason, make an effort to develop an
appropriate approach to every problem; yet always engage your critical analysis
skills in the process of the solution. If physics problems were a mere matter
of following a foolproof, 5-step formula or
using some memorized algorithm, then we wouldn't call them "problems."
Check Your Understanding
Use your understanding of Newton's second law and circular
motion principles to determine the unknown values in the following practice
problems. Click the button to check your answers.
1. A 1.50-kg bucket of water is tied by a rope and whirled in
a circle with a radius of 1.00 m. At the top of the circular loop, the speed of
the bucket is 4.00 m/s. Determine the acceleration, the net force and the
individual force values when the bucket is at the top of the circular loop.
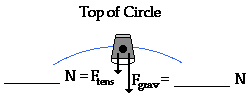
m = 1.5 kg
a = ________ m/s/s
Fnet = _________ N
Fgrav = m • g = 14.7 N (g
is 9.8 m/s/s)
a = v2 / R = (4 • Fgrav)/1
= 16 m/s/s
Fnet = m • a = 1.5 kg •16
m/s/s = 24 N, down
Fnet = Fgrav + Ftens,
so
Ftens = Fnet - Fgrav
Ftens = 24 N - 14.7 N
= 9.3 N
2. A 1.50-kg bucket of water is tied by a rope and whirled in
a circle with a radius of 1.00 m. At the bottom of the circular loop, the speed
of the bucket is 6.00 m/s. Determine the acceleration, the net force and the
individual force values when the bucket is at the bottom of the circular loop.
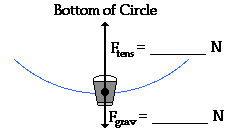
m = 1.5 kg
a = ________ m/s/s
Fnet = _________ N
Fgrav = m • g = 14.7 N (g
is 9.8 m/s/s)
a = v2 / R = (62) / 1
a = 36 m/s/s
Fnet = m • a = 1.5 kg • 36
m/s/s
Fnet = 54 N, up
Fnet = Ftens - Fgrav,
so
Ftens = Fnet + Fgrav
Ftens = 54 N +14.7 N
= 68.7 N