Acceleration

An object moving in uniform circular motion is moving in a circle with a uniform or constant speed. The velocity vector is constant in magnitude but changing in direction. Because the speed is constant for such a motion, many students have the misconception that there is no acceleration. "After all," they might say, "if I were driving a car in a circle at a constant speed of 20 mi/hr, then the speed is neither decreasing nor increasing; therefore there must not be an acceleration." At the center of this common student misconception is the wrong belief that acceleration has to do with speed and not with velocity. But the fact is that an accelerating object is an object that is changing its velocity. And since velocity is a vector that has both magnitude and direction, a change in either the magnitude or the direction constitutes a change in the velocity. For this reason, it can be safely concluded that an object moving in a circle at constant speed is indeed accelerating. It is accelerating because the direction of the velocity vector is changing.

Geometric Proof of Inward Acceleration

To understand this at a deeper level, we will have to combine the definition of acceleration with a review of some basic vector principles. that acceleration as a quantity was defined as the rate at which the velocity of an object changes. As such, it is calculated using the following equation:

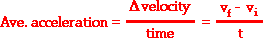
where v_i represents the initial velocity and v_f represents the final velocity after some time of t. The numerator of the equation is found by subtracting one vector (v_i) from a second vector (v_f). But the addition and subtraction of vectors from each other is done in a manner much different than the addition and subtraction of scalar quantities. Consider the case of an object moving in a circle about point C as shown in the diagram below. In a time of t seconds, the object has moved from point A to point B. In this time, the velocity has changed from v_i to v_f. The process of subtracting v_i from v_f is shown in the vector diagram; this process yields the change in velocity.

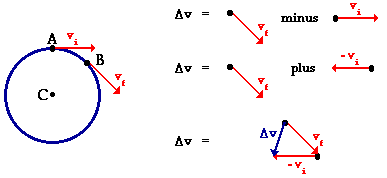
Direction of the Acceleration Vector

Note in the diagram above that there is a velocity change for an object moving in a circle with a constant speed. A careful inspection of the velocity change vector in the above diagram shows that it points down and to the left. At the midpoint along the arc connecting points A and B, the velocity change is directed towards point C - the center of the circle. The acceleration of the object is dependent upon this velocity change and is in the same direction as this velocity change. The acceleration of the object is in the same direction as the velocity change vector; the acceleration is directed towards point C as well - the center of the circle. Objects moving in circles at a constant speed accelerate towards the center of the circle.

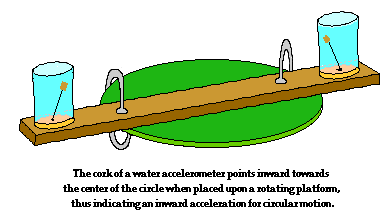
The acceleration of an object is often measured using a device known as an accelerometer. A simple accelerometer consists of an object immersed in a fluid such as water. Consider a sealed jar that is filled with water. A cork attached to the lid by a string can serve as an accelerometer. To test the direction of acceleration for an object moving in a circle, the jar can be inverted and attached to the end of a short section of a wooden 2x4. A second accelerometer constructed in the same manner can be attached to the opposite end of the 2x4. If the 2x4 and accelerometers are clamped to a rotating platform and spun in a circle, the direction of the acceleration can be clearly seen by the direction of lean of the corks. As the cork-water combination spins in a circle, the cork leans towards the center of the circle. The least massive of the two objects always leans in the direction of the acceleration. In the case of the cork and the water, the cork is less massive (on a per mL basis) and thus it experiences the greater acceleration. Having less inertia (owing to its smaller mass on a per mL basis), the cork resists the acceleration the least and thus leans to the inside of the jar towards the center of the circle. This is observable evidence that an object moving in circular motion at constant speed experiences an acceleration that is directed towards the center of the circle.

Another simple homemade accelerometer involves a lit candle centered vertically in the middle of an open-air glass. If the glass is held level and at rest (such that there is no acceleration), then the candle flame extends in an upward direction. However, if you hold the glass-candle system with an outstretched arm and spin in a circle at a constant rate (such that the flame experiences an acceleration), then the candle flame will no longer extend vertically upwards. Instead the flame deflects from its upright position. This signifies that there is an acceleration when the flame moves in a circular path at constant speed. The deflection of the flame will be in the direction of the acceleration. This can be explained by asserting that the hot gases of the flame are less massive (on a per mL basis) and thus have less inertia than the cooler gases that surround it. Subsequently, the hotter and lighter gases of the flame experience the greater acceleration and will lean in the direction of the acceleration. A careful examination of the flame reveals that the flame will point towards the center of the circle, thus indicating that not only is there an acceleration; but that there is an inward acceleration. This is one more piece of observable evidence that indicates that objects moving in a circle at a constant speed experience an acceleration that is directed towards the center of the circle.

So thus far, we have seen a geometric proof and two real-world demonstrations of this inward acceleration. At this point it becomes the decision of the student to believe or to not believe. Is it sensible that an object moving in a circle experiences an acceleration that is directed towards the center of the circle? Can you think of a logical reason to believe in say no acceleration or even an outward acceleration experienced by an object moving in uniform circular motion? In the next TOPIC, additional logical evidence will be presented to support the notion of an inward force for an object moving in circular motion.

Check Your Understanding

1. The initial and final speed of a ball at two different points in time is shown below. The direction of the ball is indicated by the arrow. For each case, indicate if there is an acceleration. Explain why or why not. Indicate the direction of the acceleration.

a.
Acceleration: Yes or No? Explain.	If there is an acceleration, then what direction is it?
See Answer Since the velocity did not change, there is no acceleration.	See Answer There is no acceleration.

b.
Acceleration: Yes or No? Explain.	If there is an acceleration, then what direction is it?
See Answer Since the velocity changed (the object increased its speed), there is an acceleration.	See Answer If a rightward-moving object speeds up, then it experiences a rightward acceleration.

c.
Acceleration: Yes or No? Explain.	If there is an acceleration, then what direction is it?
See Answer Since the velocity changed (the object decreased its speed), there is an acceleration.	See Answer If a rightward-moving object slows down, then it experiences a leftward acceleration. close

d.
Acceleration: Yes or No? Explain.	If there is an acceleration, then what direction is it?
See Answer Since the velocity changed (the object decreased its speed), there is an acceleration.	See Answer If a rightward-moving object slows down, then it experiences a leftward acceleration.

e.
Acceleration: Yes or No? Explain.	If there is an acceleration, then what direction is it?
See Answer	See Answer

The object was moving rightward and slowed down to 0 m/s before changing directions and speeding up while traveling leftward. This constitutes a leftward acceleration.

Yes. Even though the initial and final speeds are the same, there has been a change in direction for the object. Thus, there is an acceleration.

close

2. Explain the connection between your answers to the above questions and the reasoning used to explain why an object moving in a circle at constant speed can be said to experience an acceleration.

See Answer

An object which experiences either a change in the magnitude or the direction of the velocity vector can be said to be accelerating. This explains why an object moving in a circle at constant speed can be said to accelerate - the direction of the velocity changes.

3. Dizzy Smith and Hector Vector are still discussing #1e. Dizzy says that the ball is not accelerating because its velocity is not changing. Hector says that since the ball has changed its direction, there is an acceleration. Who do you agree with? Argue a position by explaining the discrepancy in the other student's argument.

See Answer

Agree with Hector. A change in direction constitutes a velocity change and therefore an acceleration.

4. Identify the three controls on an automobile that allow the car to be accelerated.

See Answer

The accelerator allows the car to increase speed. The brake pedal allows the car to decrease the speed. And the steering wheel allows the car to change direction.

close

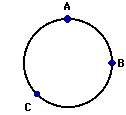For questions #5-#8: An object is moving in a clockwise direction around a circle at constant speed. Use your understanding of the concepts of velocity and acceleration to answer the next four questions. Use the diagram shown at the right.

5. Which vector below represents the direction of the velocity vector when the object is located at point B on the circle?

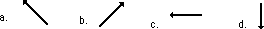
6. Which vector below represents the direction of the acceleration vector when the object is located at point C on the circle?

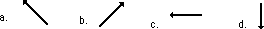
7. Which vector below represents the direction of the velocity vector when the object is located at point C on the circle?

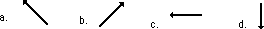
8. Which vector below represents the direction of the acceleration vector when the object is located at point A on the circle?

See Answer

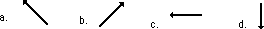
5.  Answer = D

The velocity vector is directed tangent to the circle; that would be downward towards the center when at the object is at point B.

6.  Answer = B

The acceleration vector is directed towards the center; that would be up and to the right when the object is at point C.

7.  Answer = A

The velocity vector is directed tangent to the circle; that would be upwards and leftwards when at point C

8. Answer = D

The acceleration vector is directed towards the center; that would be straight down when the object is at point A.