Circular Motion and Satellite Motion

Motion Characteristics for Circular Motion

Speed and Velocity

Any moving object can be described using the kinematic concepts discussed in previously The motion of a moving object can be explained using either Newton's Laws and vector principles or by means of the Work-Energy Theorem The same concepts and principles used to describe and explain the motion of an object can be used to describe and explain the parabolic motion of a projectile. In this unit, we will see that these same concepts and principles can also be used to describe and explain the motion of objects that either move in circles or can be approximated to be moving in circles. Kinematic concepts and motion principles will be applied to the motion of objects in circles and then extended to analyze the motion of such objects as roller coaster cars, a football player making a circularturn, and a planet orbiting the sun. We will see that the beauty and power of physics lies in the fact that a few simple concepts and principles can be used to explain the mechanics of the entire universe. Lesson 1 of this study will begin with the development of kinematic and dynamic ideas that can be used to describe and explain the motion of objects in circles.

Suppose that you were driving a car with the steering wheel turned in such a manner that your car followed the path of a perfect circle with a constant radius. And suppose that as you drove, your speedometer maintained a constant reading of 10 mi/hr. In such a situation as this, the motion of your car could be described as experiencing uniform circular motion. Uniform circular motion is the motion of an object in a circle with a constant or uniform speed.

Calculation of the Average Speed

Uniform circular motion - circular motion at a constant speed - is one of many forms of circular motion. An object moving in uniform circular motion would cover the same linear distance in each second of time. When moving in a circle, an object traverses a distance around the perimeter of the circle. So if your car were to move in a circle with a constant speed of 5 m/s, then the car would travel 5 meters along the perimeter of the circle in each second of time. The distance of one complete cycle around the perimeter of a circle is known as the circumference. With a uniform speed of 5 m/s, a car could make a complete cycle around a circle that had a circumference of 5 meters. At this uniform speed of 5 m/s, each cycle around the 5-m circumference circle would require 1 second. At 5 m/s, a circle with a circumference of 20 meters could be made in 4 seconds; and at this uniform speed, every cycle around the 20-m circumference of the circle would take the same time period of 4 seconds. This relationship between the circumference of a circle, the time to complete one cycle around the circle, and the speed of the object is merely an extension of the average speed equation elaborated in last topic.

The circumference of any circle can be computed using from the radius according to the equation

Circumference = 2*pi*Radius

Combining these two equations above will lead to a new equation relating the speed of an object moving in uniform circular motion to the radius of the circle and the time to make one cycle around the circle (period).

where R represents the radius of the circle and T represents the period. This equation, like all equations, can be used as an algebraic recipe for problem solving. It also can be used to guide our thinking about the variables in 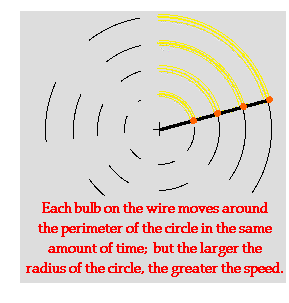the equation relate to each other. For instance, the equation suggests that for objects moving around circles of different radius in the same period, the object traversing the circle of larger radius must be traveling with the greatest speed. In fact, the average speed and the radius of the circle are directly proportional. A twofold increase in radius corresponds to a twofold increase in speed; a threefold increase in radius corresponds to a three--fold increase in speed; and so on. To illustrate, consider a strand of four LED lights positioned at various locations along the strand. The strand is held at one end and spun rapidly in a circle. Each LED light traverses a circle of different radius. Yet since they are connected to the same wire, their period of rotation is the same. Subsequently, the LEDs that are further from the center of the circle are traveling faster in order to sweep out the circumference of the larger circle in the same amount of time. If the room lights are turned off, the LEDs created an arc that could be perceived to be longer for those LEDs that were traveling faster - the LEDs with the greatest radius. This is illustrated in the diagram at the right.

The Direction of the Velocity Vector

Objects moving in uniform circular motion will have a constant speed. But does this mean that they will have a constant velocity? Recall it as discussed early that speed and velocity refer to two distinctly different quantities. Speed is a scalar quantity and velocity is a vector quantity. Velocity, being a vector, has both a magnitude and a direction. The magnitude of the velocity vector is the instantaneous speed of the object. The direction of th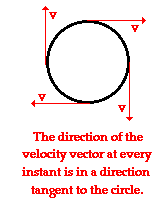e velocity vector is directed in the same direction that the object moves. Since an object is moving in a circle, its direction is continuously changing. At one moment, the object is moving northward such that the velocity vector is directed northward. One quarter of a cycle later, the object would be moving eastward such that the velocity vector is directed eastward. As the object rounds the circle, the direction of the velocity vector is different than it was the instant before. So while the magnitude of the velocity vector may be constant, the direction of the velocity vector is changing. The best word that can be used to describe the direction of the velocity vector is the word tangential. The direction of the velocity vector at any instant is in the direction of a tangent line drawn to the circle at the object's location. (A tangent line is a line that touches a circle at one point but does not intersect it.) The diagram at the right shows the direction of the velocity vector at four different points for an object moving in a clockwise direction around a circle. While the actual direction of the object (and thus, of the velocity vector) is changing, its direction is always tangent to the circle.

To summarize, an object moving in uniform circular motion is moving around the perimeter of the circle with a constant speed. While the speed of the object is constant, its velocity is changing. Velocity, being a vector, has a constant magnitude but a changing direction. The direction is always directed tangent to the circle and as the object turns the circle, the tangent line is always pointing in a new direction.

Check Your Understanding

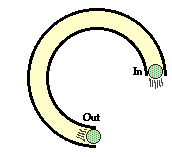1. A tube is been placed upon the table and shaped into a three-quarters circle. A golf ball is pushed into the tube at one end at high speed. The ball rolls through the tube and exits at the opposite end. Describe the path of the golf ball as it exits the tube.

See Answer

The ball will move along a path which is tangent to the spiral at the point where it exits the tube. At that point, the ball will no longer curve or spiral, but rather travel in a straight line in the tangential direction.