Bar Chart Illustrations
One tool which can be utilized to express an understanding of
the work-energy theorem is a bar chart. A work-energy bar chart represents the
amount of energy possessed by an object by means of a vertical bar. The length
of the bar is representative of the amount of energy present, with a longer bar
representing a greater amount of energy. In a work-energy bar chart, a bar is
constructed for each form of energy. Consistent with the work-energy
relationship discussed in this lesson, the sum of all
forms of initial energy plus the work done on the object by external forces
equals the sum of all forms of final energy.
KEi + PEi + Wext = KEf + PEf
In a work-energy bar chart, a bar is used to represent the
amount of each term in the above equation. Consequently, the sum of the bar
heights for the initial condition (initial energy + external work) must equal
the sum of the bar heights for the final condition (final energy). Since the potential
energy comes in two forms - the elastic potential energy stored in
springs (PEspring) and the gravitational potential energy (PEgrav) - the above equation is
rewritten as
KEi + PEi-grav + PEi-spring + Wext = KEf + PEf-grav + PEf-spring
In this portion of Lesson 2, we will investigate the use and
meaning of work-energy bar charts and make an effort to apply this
understanding to a variety of motions involving energy changes or energy
transformations.
Procedure
for Constructing Bar Charts
The following procedure might be useful for constructing
work-energy bar charts:
· analyze the initial and final states of the
object in order to make decisions about the presence or absence of the
different forms of energy
· analyze the forces acting upon the object during the motion to determine if external forces are doing work and whether the work (if present) is positive or negative
· construct
bars on the chart to illustrate the presence and absence of the various forms
of energy for the initial and final state of the object; the exact height of
the individual bars is not important; what is important is that the sum of the
heights on the left of the chart is balanced
by the sum of the heights on
the right of the chart
The above procedure is illustrated below.
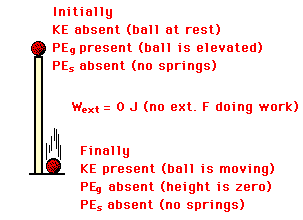 Consider a ball falling from the top of a pillar to the ground below;
ignore air resistance. The initial state is the ball at rest on top of the
pillar and the final state is the ball just prior to
striking the ground. Given this motion and the identification of the initial
and final state of the ball, decisions can be made about the presence and
absence of each form of energy. Since there is no motion at the top of the
pillar, there is no initialkinetic energy. Since the ball
is elevated above the ground while on top of the pillar, there is an initial gravitational
potential energy (PEgrav). There are no springs involved; thus, there is neither initial nor
final elastic potential energy (PEspring). In the final condition (just prior to
striking the ground), the ball is moving. Thus, there is a final kinetic
energy. And finally, the ball is no longer elevated above the ground so there
is no final gravitational potential energy. The ball falls under the influence
of gravity (an internal force) alone. Thus there are noexternal forces
present nor doing work. The diagram at the right
summarizes this analysis.
Consider a ball falling from the top of a pillar to the ground below;
ignore air resistance. The initial state is the ball at rest on top of the
pillar and the final state is the ball just prior to
striking the ground. Given this motion and the identification of the initial
and final state of the ball, decisions can be made about the presence and
absence of each form of energy. Since there is no motion at the top of the
pillar, there is no initialkinetic energy. Since the ball
is elevated above the ground while on top of the pillar, there is an initial gravitational
potential energy (PEgrav). There are no springs involved; thus, there is neither initial nor
final elastic potential energy (PEspring). In the final condition (just prior to
striking the ground), the ball is moving. Thus, there is a final kinetic
energy. And finally, the ball is no longer elevated above the ground so there
is no final gravitational potential energy. The ball falls under the influence
of gravity (an internal force) alone. Thus there are noexternal forces
present nor doing work. The diagram at the right
summarizes this analysis.
To complete the bar chart, an arbitrarily
decided height for each bar is decided upon and a bar is constructed for each
form of energy. As mentioned before, it is not important exactly how high each
bar is. It is only important that the sum of the bar heights on the left balance the sum of
the bar heights on the right.
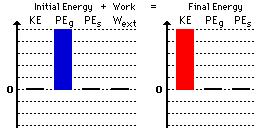
Observe that this work-energy bar chart reveals that
· there is
no kinetic and elastic potential energy in the initial state
· there is
no gravitational and elastic potential energy in the final state
· there is
no work done by external forces
· the sum of
the heights on the right (5 units) equals the sum of the heights on the left (5
units)
It is not important as to how high the two bars are in the
above bar chart. If the bars were 4 units high instead of 5 units high, then it
would be an equally acceptable bar chart. The decision about bar height is
entirely arbitrary.
|
Perhaps
at this time you may want to review the lessons on work, potential energy and
kinetic energy. Use the links below. · Work · Potential Energy · Kinetic Energy |
The
Example of a Skidding Car
Now we will repeat the process for a car which skids from a
high speed to a stop across level ground with its brakes applied. The initial
state is the car traveling at a high speed and the final state is the car at
rest. Initially, the car has kinetic energy (since it is moving) but does
not have gravitational potential energy (since the height is zero) or elastic
potential energy (since there are no springs). In the
final state of the car, there is neither kinetic energy (since the car is at
rest) nor potential energy (since there is no height nor springs). The force of
friction between the tires of the skidding car and the road does work on
the car.Friction is an external force. Friction does negative work since its
direction is opposite the direction of the car's motion.

Now that the analysis is complete, the bar chart can be
constructed. The chart must be consistent with the above analysis.
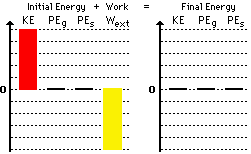
Observe that the bar for work is a downward bar. This is
consistent with the fact that the work done by friction is negative work.
Whenever negative work is done by external forces, the Wext bar will
be a downward bar. Note also that the sum of the bar height on the left side
(+5 plus -5) is the same as the sum of the bar heights on the right side of the
chart. One final comment is in order: even though the height of all bars on the
left equals the height of all bars on the right, energy is not conserved.
The bar chart includes both energy and work on the left side of the chart. If
work is done by external forces, then the only reason that the sum of the
bar heights are equal on both sides is that the Wext makes up for the difference between the initial
and final amounts of total mechanical energy.
|
Perhaps
at this time you may want to review the lessons on work, potential energy and
kinetic energy. Use the links below. · Work · Potential Energy · Kinetic Energy |
The
Example of a Skier
As a final example consider a skier that starts from rest on
top of hill A and skis into the valley and back up onto hill B. The skier
utilizes her poles to propel herself across the snow, thus doing work to change
her total mechanical energy. The initial state is on top of hill A and the
final state is on top of hill B. Suppose that friction and air resistance have
a negligible effect on the motion. In the initial state, the skier has nokinetic energy (the skier
is said to be at rest). There is no elastic potential energy in both
the initial and the final states (since there are no springs). The skier has gravitational
potential energy in both the initial and the final states (since
the skier is at an elevated position). Finally, work is being done by external
forces since the skier is said to be using "her poles to propel herself
across the snow." This work is positive work since the force of the snow
on her poles is in the same direction as her displacement.
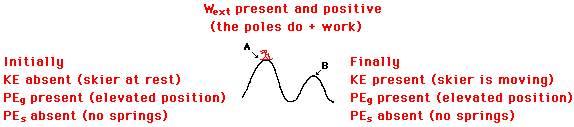
Now that the analysis is complete, the bar charts can be
constructed. The charts must be consistent with the above analysis.
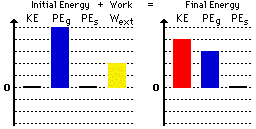
Observe that the bar for work is an upward bar. This is
consistent with the fact that the work done by the poles is positive work.
Whenever positive work is done by external forces, the Wext bar will
be an upward bar. Note also that the sum of the bar height on the left side (+5
plus +2) is the same as the sum of the bar heights on the right side (+4 plus
+3) of the chart. As mentioned earlier, the exact heights of the individual
bars are not important. It is only important that the bars exist, that they are
in the correct direction (upward) and that their sum on the left is the same as
the sum on the right.
|
Perhaps
at this time you may want to review the lessons on work, potential energy and
kinetic energy. Use the links below. · Work · Potential Energy · Kinetic Energy |
A
Different Type of Bar Chart
On occasions it is customary to utilize a different type of
work-energy bar chart that looks like the diagram below. If external forces are
not doing work, then the total mechanical energy is conserved. The Wext term
cancels from the work-energy equation leaving the equation
KEi + PEi = KEf + PEf
This equation shows that the total
mechanical energy (potential energy plus kinetic energy) is the
same in the initial state as it is in the final state. In fact, if external
forces are not doing work, then the total mechanical energy will be the same
throughout the entire motion. For such situations it is
customary to use the different style of bar chart to depict energy
conservation. A series of bars are shown for a variety of positions throughout
the motion; each set of bars reveals that the total mechanical energy (TME) is
always the same while the potential energy (PE) and the kinetic energy (KE) are
constantly changing.

As an example of the use of this bar chart,
consider a roller coaster car in the ideal situation in which the force of air
resistance is assumed negligible (indeed, an idealized situation). Since the
normal force acts at right angles to the motion at all times, it does not do
work. The only force doing work on the roller coaster car is gravity. And since
the force of gravity is an internal or conservative force, the total mechanical
energy is conserved (i.e., not changing). The energy may change forms -
transforming from potential to kinetic and vice versa. Yet the total amount
will never change. The diagram below depicts the conservation of total mechanical
energy and the transformation of potential and kinetic energy for a roller
coaster car at five positions along a track.
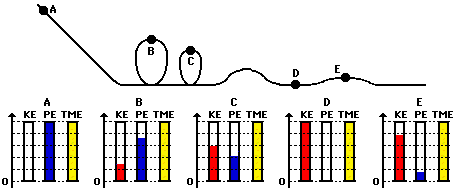
In conclusion, bar charts are a useful tool for depicting the
influence of external forces (if present) upon the total mechanical energy. It
is a conceptual tool for representing one's understanding of the work-energy
relationship.
Check Your Understanding
Construct analyses and work-energy bar charts for the
following motions. Then check the answers by clicking the button and by
clicking on the See Bar Chart link.
1. A ball is dropped from rest from a bridge.
As the ball falls through the air, it encounters a small amount of air
resistance. The final state of the ball is the instant before it strikes the
water.
2. A volleyball player spikes the ball at just
above net level and drives it over the net. The initial state is the ball just
prior to the spike. The final state of the ball is the instant before it
strikes the ground.
3. A spring gun is used to project a sponge
dart into the air at an angle to the horizontal. The gun is held at a height of
1-meter before the trigger is pulled.
The loaded spring gun is the initial state and the sponge dart at its peak is
the final state.
4. A baseball is caught by a catcher after
passing over home plate. The initial state is the baseball moving at high speed
just prior to hitting the catcher's mitt. The final state is the baseball just
after the catcher has applied the force to stop the ball. Assume that the ball
does not change height as the catcher is catching it.
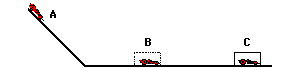 5. In a physics lab, a Hot Wheels car starts at an elevated position,
moves down an incline to the level ground, strikes a box and skids to a stop.
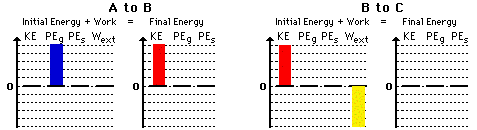
Consider three states for the car: state A is the top of the incline; state B
is the bottom of the incline before striking the box; state C is after the car
has been brought to a stop. Use the diagram at the right and your understanding
of the work-energy theorem to construct bar charts for the motion from A to B
and from B to C.
5. In a physics lab, a Hot Wheels car starts at an elevated position,
moves down an incline to the level ground, strikes a box and skids to a stop.
Consider three states for the car: state A is the top of the incline; state B
is the bottom of the incline before striking the box; state C is after the car
has been brought to a stop. Use the diagram at the right and your understanding
of the work-energy theorem to construct bar charts for the motion from A to B
and from B to C.
Answers to Above Questions
1. Here is the bar chart for question #1 above.
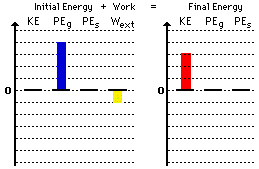
2. Here is the bar chart for question #2 above.
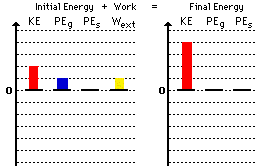
3. Here is the bar chart for question #3 above.
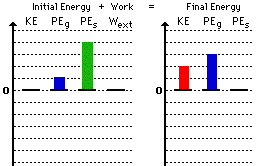
4. Here is the bar chart for question #4 above.
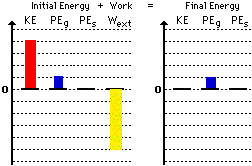
5. Here is the bar chart for question #5 above.