Equal and Opposite Momentum Changes

Just like in collisions, the two objects involved encounter the same force for the same amount of time directed in opposite directions. This results in impulses that are equal in magnitude and opposite in direction. And since an impulse causes and is equal to a change in momentum, both carts encounter momentum changes that are equal in magnitude and opposite in direction. If the exploding system includes two objects or two parts, this principle can be stated in the form of an equation as:

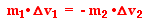
If the masses of the two objects are equal, then their post-explosion velocity will be equal in magnitude (assuming the system is initially at rest). If the masses of the two objects are unequal, then they will be set in motion by the explosion with different speeds. Yet even if the masses of the two objects are different, the momentum change of the two objects (mass • velocity change) will be equal in magnitude.

The diagram below depicts a variety of situations involving explosion-like impulses acting between two carts on a low-friction track. The mass of the carts is different in each situation. In each situation, total system momentum is conserved as the momentum change of one cart is equal and opposite the momentum change of the other cart.

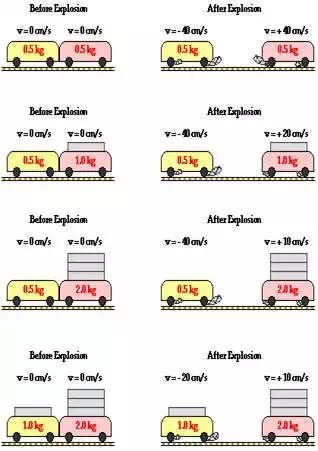
In each of the above situations, the impulse on the carts is the same - a value of 20 kg•cm/s (or cN•s). Since the same spring is used, the same impulse is delivered. Thus, each cart encounters the same momentum change in every situation - a value of 20 kg•cm/s. For the same momentum change, an object with twice the mass will encounter one-half the velocity change. And an object with four times the mass will encounter one-fourth the velocity change.