Momentum Conservation in Explosions

As discussed in a previous part of Lesson 2, total system momentum is conserved for collisions between objects in an isolated system. For collisions occurring in isolated systems, there are no exceptions to this law. This same principle of momentum conservation can be applied to explosions. In an explosion, an internal impulse acts in order to propel the parts of a system (often a single object) into a variety of directions. After the explosion, the individual parts of the system (that is often a collection of fragments from the original object) have momentum. If the vector sum of all individual parts of the system could be added together to determine the total momentum after the explosion, then it should be the same as the total momentum before the explosion. Just like in collisions, total system momentum is conserved.

Momentum conservation is often demonstrated in a Physics class with a homemade cannon demonstration. A homemade cannon is placed upon a cart and loaded with a tennis ball. The cannon is equipped with a reaction chamber into which a small amount of fuel is inserted. The fuel is ignited, setting off an explosion that propels the tennis ball through the muzzle of the cannon. The impulse of the explosion changes the momentum of the tennis ball as it exits the muzzle at high speed. The cannon experienced the same impulse, changing its momentum from zero to a final value as it recoils backwards. Due to the relatively larger mass of the cannon, its backwards recoil speed is considerably less than the forward speed of the tennis ball.

In the exploding cannon demonstration, total system momentum is conserved. The system consists of two objects - a cannon and a tennis ball. Before the explosion, the total momentum of the system is zero since the cannon and the tennis ball located inside of it are both at rest. After the explosion, the total momentum of the system must still be zero. If the ball acquires 50 units of forward momentum, then the cannon acquires 50 units of backwards momentum. The vector sum of the individual momenta of the two objects is 0. Total system momentum is conserved.

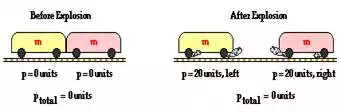
As another demonstration of momentum conservation, consider two low-friction carts at rest on a track. The system consists of the two individual carts initially at rest. The total momentum of the system is zero before the explosion. One of the carts is equipped with a spring-loaded plunger that can be released by tapping on a small pin. The spring is compressed and the carts are placed next to each other. The pin is tapped, the plunger is released, and an explosion-like impulse sets both carts in motion along the track in opposite directions. One cart acquires a rightward momentum while the other cart acquires a leftward momentum. If 20 units of forward momentum are acquired by the rightward-moving cart, then 20 units of backwards momentum is acquired by the leftward-moving cart. The vector sum of the momentum of the individual carts is 0 units. Total system momentum is conserved.