Using Equations as a Guide to Thinking
The three problems on the previous
page illustrate how the law of momentum conservation can be used to solve
problems in which the after-collision velocity of an object is predicted based
on mass and velocity information. There are similar
practice problems (with accompanying solutions) lower on
this page that are worth the practice. However, let's first take a more
qualitative approach to some collision problems. The questions that follow
provide a real test of your conceptual understanding of momentum conservation in
collisions.
Suppose that you have joined NASA and are enjoying your
first space walk. You are outside the space
shuttle when your fellow astronaut of approximately equal mass is moving
towards you at 2 m/s (with respect to the shuttle). If she collides with you
and holds onto you, then how fast (with respect to the shuttle do you both move
after the collision?
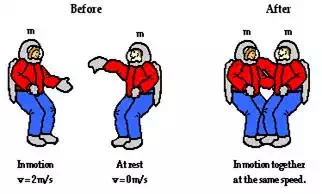
This problem could be solved in the usual manner with a
momentum table; the variable m could be used for the mass of the astronauts or
any random number could be used for the mass of the astronauts (provided each
astronaut had the same mass). In the process of solving the problem, the mass
would cancel out of the momentum conservation equation and the post-collision
velocities could be determined. However, there is a more  conceptual means of solving this problem. In order for the momentum
before the collision to be equal to the momentum after the collision, the after
collision velocity must be smaller than the before collision velocity. How many
times smaller must it be? By what factor must the velocity be decreased? Before
the collision, the amount of mass in motion is m; after the collision, the amount of mass in motion is 2•m. The amount of mass in motion has doubled as the result of the
collision. If the mass is increased by a factor of two, then the velocity must
be decreased by a factor of 2. The before-collision velocity was 2 m/s so the
after-collision velocity must be one-half this value: 1 m/s. Each astronaut is
moving with a velocity of 1 m/s after the collision.
conceptual means of solving this problem. In order for the momentum
before the collision to be equal to the momentum after the collision, the after
collision velocity must be smaller than the before collision velocity. How many
times smaller must it be? By what factor must the velocity be decreased? Before
the collision, the amount of mass in motion is m; after the collision, the amount of mass in motion is 2•m. The amount of mass in motion has doubled as the result of the
collision. If the mass is increased by a factor of two, then the velocity must
be decreased by a factor of 2. The before-collision velocity was 2 m/s so the
after-collision velocity must be one-half this value: 1 m/s. Each astronaut is
moving with a velocity of 1 m/s after the collision.
The process of solving this problem involved using a
conceptual understanding of the equation formomentum (p=m*v). This
equation becomes a guide to thinking about how a change in one variable affects
a change in another variable. The constant quantity in a collision is the
momentum (momentum is conserved). For a constant momentum value, mass and
velocity are inversely proportional. Thus, an increase in mass results in a
decrease in velocity.
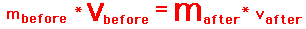
A twofold increase in mass, results in a twofold decrease in
velocity (the velocity is one-half its original value); a threefold increase in
mass results in a threefold decrease in velocity (the velocity is one-third its
original value); etc. Of course, it is instructive to point out that this form
of problem solving is limited to situations in which one of the two objects is
at rest before the collision and both objects move at the same speed after the
collision. To further test your understanding of this type of quantitative
reasoning, try the following two questions.
A large fish is in motion at 2 m/s when it encounters a
smaller fish that is at rest. The large fish swallows the smaller fish and
continues in motion at a reduced speed. If the large fish has three times the
mass of the smaller fish, then what is the speed of the large fish (and the
smaller fish) after the collision? Click the button to view answer.
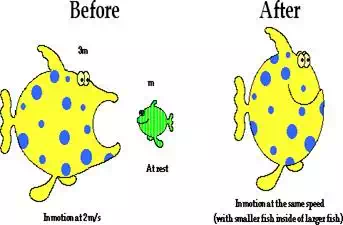

v = 1.5 m/s
Solve using a
table or by the following method: The amount of mass in motion is increased
from 3m to 4m (3m + m); that is mass is increased by a factor of 4/3 (1.33). To
conserve momentum, an increase in mass by a factor of 1.33 must be accompanied
by a decrease in velocity by a factor of 1.33. Thus divide the original
velocity of 2 m/s by 1.33.
Still another
method:
3*m*2 = (3*m +
m)*v
6*m = 4*m*v
(6*m) / (4*m) = v
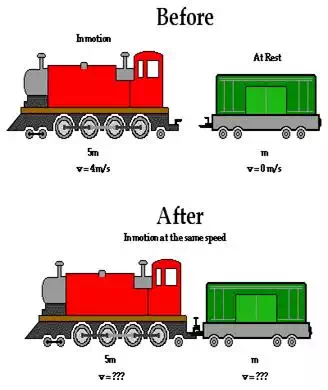
A railroad diesel engine has five times the mass of a boxcar.
A diesel coasts backwards along the track at 4 m/s and couples together with
the boxcar (initially at rest). How fast do the two trains cars coast after
they have coupled together? Click the button to view answer.
Check Your Understanding
Express your understanding of the concept and mathematics of
momentum conservation by answering the following questions. Assume isolated
systems and momentum conservation for each problem. Click the See Answer button
to view answer. (If necessary, return to the instructional
page on solving collision analysis problems.)
1. In a physics lab, 0.500-kg cart (Cart A)
moving rightward with a speed of 92.8 cm/s collides with a 1.50-kg cart (Cart
B) moving leftward with a speed of 21.6 cm/s. The two carts stick together and
move as a single object after the collision. Determine the post-collision speed
of the two carts.
See Solution
2. A 25.0-gram bullet enters a 2.35-kg
watermelon and embeds itself in the melon. The melon is immediately set into
motion with a speed of 3.82 m/s. The bullet remains lodged inside the melon.
What was the entry speed of the bullet? (CAUTION: Be careful of the units on
mass.)
See Solution
3. A 25.0-gram bullet enters a 2.35-kg
watermelon with a speed of 217 m/s and exits the opposite side with a speed of
109 m/s. If the melon was originally at rest, then what speed will it have as
the bullet leaves its opposite side? (CAUTION: Be careful of the units on mass.)
See Solution
4. In a physics lab, a 0.500-kg cart (Cart A)
moving with a speed of 129 cm/s encounters a magnetic
collision with a 1.50-kg cart (Cart B) that is initially at rest. The 0.500-kg
cart rebounds with a speed of 45 cm/s in the opposite direction. Determine the
post-collision speed of the 1.50-kg cart.
See Solution
5. A 3000-kg truck moving rightward with a
speed of 5 km/hr collides head-on with a 1000-kg car moving leftward with a
speed of 10 km/hr. The two vehicles stick together and move
with the same velocity after the collision. Determine the post-collision
velocity of the car and truck. (CAREFUL: Be cautious of the
+/- sign on the velocity of the two vehicles.)
See Solution
6. During a goal-line stand, a 75-kg fullback moving eastward
with a speed of 8 m/s collides head-on with a 100-kg lineman moving westward
with a speed of 4 m/s. The two players collide and stick
together, moving at the same velocity after the
collision. Determine the post-collision velocity of the two players. (CAREFUL: Be cautious of the +/- sign
on the velocity of the two players.)
See Solution
Answers
1. The problem can be solved using a momentum
table:
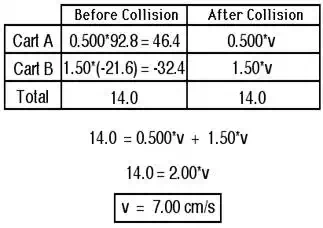
Return to Question
2. The problem can be solved using a momentum
table:
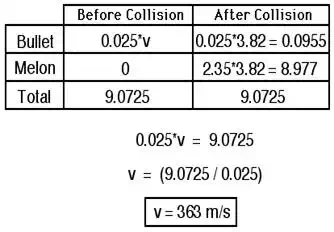
Return to Question
3. The problem can be solved using a momentum
table:
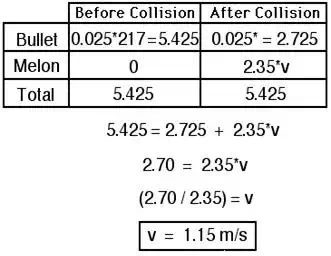
Return to Question
4. The problem can be solved using a momentum
table:
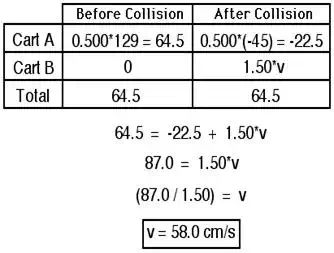
Return to Question
5. The problem can be solved using a momentum
table:

Return to Question
6. The problem can be solved using a momentum
table:

Return to Question