Equilibrium and Statics
When all the forces that act upon an object are
balanced, then the object is said to be in a state of equilibrium. The forces are considered to be balanced if the
rightward forces are balanced by the leftward forces and the upward forces are
balanced by the downward forces. This however does not necessarily mean that
all the forces are equal to each
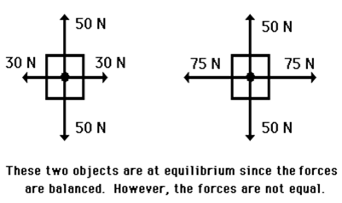
other. Consider the two objects pictured in the force diagram shown below. Note
that the two objects are at equilibrium because the forces that act upon them
are balanced; however, the individual forces are not equal to each other. The
50 N force is not equal to the 30 N force.
If an object is at equilibrium, then the forces are balanced. Balanced is the key
word that is used to describe equilibrium situations. Thus, the net force is
zero and the acceleration is 0 m/s/s. Objects at equilibrium must have an
acceleration of 0 m/s/s. This extends from Newton's
first law of motion. But having an acceleration of 0 m/s/s does
not mean the object is at rest. An object at equilibrium is either ...
· at rest
and staying at rest, or
· in motion and continuing in motion with the
same speed and direction.
This too extends from Newton's
first law of motion.
Analyzing a Static
Equilibrium Situation
If an object is at rest and is in a state of equilibrium,
then we would say that the object is at "static equilibrium."
"Static" means stationary or at rest. A common physics lab is to hang an object by two or more strings and
to measure the forces that are exerted at angles upon the object to support its
weight. The state of the object is analyzed in
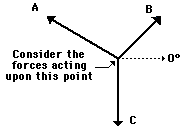
terms of the forces acting upon the object. The object
is a point on a string upon which three forces were
acting. See diagram at right. If the object is at equilibrium, then the net
force acting upon the object should be 0 Newton. Thus, if all the forces are
added together as vectors, then the resultant force (the
vector sum) should be 0 Newton. (Recall that the net force is
"the vector sum of all the forces" or the
resultant of adding all the individual forces head-to-tail.) Thus, an
accurately drawn vector addition diagram can be constructed to determine the
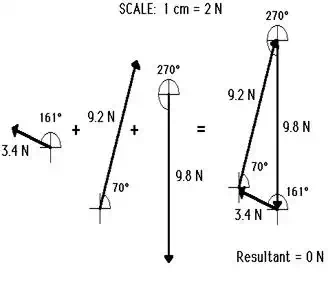
resultant. Sample data for such a lab are shown below.
|
|
|
For most students, the resultant was 0 Newton (or at least very close to 0 N).
This is what we expected - since the object was at equilibrium, the net force (vector sum of all the forces) should be 0 N.
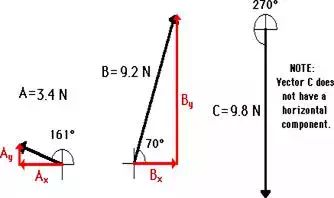
Another way of determining the net force (vector sum of all
the forces) involves using the trigonometric functions to resolve each
force into its horizontal and vertical components. Once the components are
known, they can be compared to see if the vertical forces are balanced and if
the horizontal forces are balanced. The diagram below shows vectors A, B, and C
and their respective components. For vectors A and B, the vertical components
can be determined using the sine of the angle and the horizontal components can
be analyzed using the cosine of the angle.
The magnitude and direction of each component for the sample data are shown in
the table below the diagram.
The data in the table above show that the forces nearly balance.
An analysis of the horizontal components shows that the leftward component of A nearly balances
the rightward component of B. An analysis of the vertical components show that
the sum of the upward components of A + B nearly balance
the downward component of C. The vector sum of all the forces is (nearly)
equal to 0 Newton. But what about the 0.1 N difference between rightward and
leftward forces and the 0.2 N difference between the upward and downward
forces? Why do the components of force only nearly balance?
The sample data used in this analysis are the result of measured data from an
actual experimental setup. The difference between the actual results and the
expected results is due to the error incurred when measuring force A and force
B. We would have to conclude that this low margin of experimental error
reflects an experiment with excellent results. We could say it's "close enough for government work."
Analyzing a Hanging Sign
The above analysis of the forces acting upon an object in
equilibrium is commonly used to analyze situations
involving objects at static equilibrium. The most
common application involves the analysis of the forces acting upon a sign that
is at rest. For example, consider the picture at the right that hangs on a
wall. The picture is in a state of equilibrium, and thus all the forces acting
upon the picture must be balanced. That is, all horizontal components must add
to 0 Newton and all vertical components must add to 0 Newton. The leftward pull
of cable A must balance the rightward pull of cable B and the sum of the upward
pull of cable A and cable B must balance the weight of the
sign.
Suppose the tension in both of the cables is measured to be
50 N and that the angle that each cable makes with the horizontal is known to
be 30 degrees. What is the weight of the sign? This question can be answered by
conducting a force analysis using trigonometric functions. The weight of the sign is equal to the sum of the upward components of
the tension in the two cables. Thus, a trigonometric function can be used to
determine this vertical component. A diagram and accompanying work is shown
below.
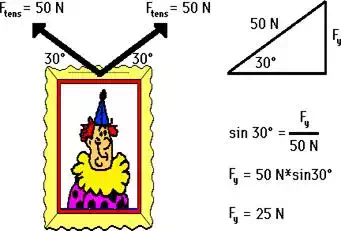
Since each cable pulls upwards with a force of 25 N, the
total upward pull of the sign is 50 N. Therefore, the force of
gravity (also known as weight) is 50 N, down. The sign weighs 50 N.
In the above problem, the tension in the
cable and the angle that the cable makes with the horizontal are
used to determine the weight of the
sign. The idea is that the tension, the angle, and the weight are related. If
the any two of these three are known, then the third quantity can be determined
using trigonometric functions.
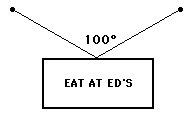As another example that illustrates this idea, consider the symmetrical
hanging of a sign as shown at the right. If the sign is known to have a mass of
5 kg and if the angle between the two cables is 100 degrees, then the tension
in the cable can be determined. Assuming that the sign is at equilibrium (a good
assumption if it is remaining at rest), the two cables must supply enough
upward force to balance the downward force of gravity. The force of
gravity (also known as weight) is 49 N (Fgrav= m*g), so each of the two cables must pull upwards
with 24.5 N of force. Since the angle between the cables is 100 degrees, then
each cable must make a 50-degree angle with the vertical and a 40-degree angle
with the horizontal. A sketch of this situation (see diagram below) reveals that
the tension in the cable can be found using the sine function. The triangle
below illustrates these relationships.
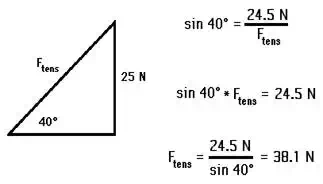
Thinking Conceptually
There is an important principle that emanates from some of
the trigonometric calculations performed above. The principle is that as the
angle with the horizontal increases, the amount of tensional force required to
hold the sign at equilibrium decreases. To illustrate this, consider a
10-Newton picture held by three different wire orientations as shown in the
diagrams below. In each case, two wires are used to support the picture; each
wire must support one-half of the sign's weight (5 N). The angle that the wires
make with the horizontal is varied from 60 degrees to 15 degrees. Use this
information and the diagram below to determine the tension in the wire for each
orientation. When finished, click the button to view the answers.
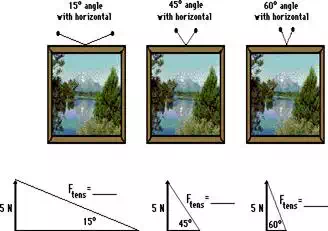
At 60 degrees, the tension is 5.8 N. (5 N / sin 60 degrees).
At 45 degrees, the tension is 7.1 N. (5 N / sin 45 degrees).
At 15 degrees,
the tension is 19.3 N (5 N / sin 15 degrees).
In conclusion, equilibrium is the state of an object in which
all the forces acting upon it are balanced. In such cases, the net force is 0
Newton. Knowing the forces acting upon an object, trigonometric functions can
be utilized to determine the horizontal and vertical components of each force.
If at equilibrium, then all the vertical components must balance and all the
horizontal components must balance.
Check Your Understanding
The following questions are meant to test your understanding
of equilibrium situations. Click the button to view the answers to these
questions.
1. The following picture is hanging on a wall. Use
trigonometric functions to determine the weight of the picture.
The weight of the sign is 42.4 N.
The tension is 30.0 N and the angle is 45 degrees. Thus,
sine (45 degrees) = (Fvert) / (30.0 N).
The proper use of algebra leads to the equation:
Fvert = (30.0 N) • sine (45
degrees) = 21.2 N
Each cable pulls
upward with 21.2 N of force. Thus, the sign must weigh twice this - 42.4 N.
2. The sign below hangs outside the physics classroom,
advertising the most important truth to be found inside. The sign is supported
by a diagonal cable and a rigid horizontal bar. If the sign has a mass of 50
kg, then determine the tension in the diagonal cable that supports its weight.
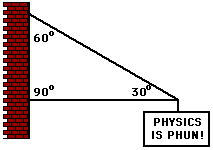
The tension is 980 Newtons.
Since the mass is 50 kg, the weight is 490 N. Since there is
only one "upward-pulling" cable, it must supply all the upward force.
This cable pulls upwards with approximately 490 N of force. Thus,
sine (30 degrees) = (490 N
) / (Ftens).
Proper use of algebra leads to the equation
Ftens = (490 N) / [ sine 30 (degrees) ] = 980 N.
3. The following sign can be found in Glenview. The sign has
a mass of 50 kg. Determine the tension in the cables.
The tension is 346 Newtons.
Since the mass is 50.0 kg, the weight is 490 N. Each cable must
pull upwards with 245 N of force.
Thus, sine (45
degrees) = (245 N ) / (Ftens).
Proper use of algebra leads to the equation
Ftens = (245 N) / [sine (45
degrees)] = 346 N.
close
4. After its most recent delivery, the infamous stork
announces the good news. If the sign has a mass of 10 kg, then what is the
tensional force in each cable? Use trigonometric functions and a sketch to
assist in the solution.
The tension 56.6 Newtons.
Since the mass is 10.0 kg, the weight is 98.0 N. Each cable must
pull upwards with 49.0 N of force. Thus,
sine 60 (degrees) = (49.0
N) / (Ftens).
Proper use of algebra leads to the equation
Ftens = (49.0 N) / [ sine 60 (degrees) ] = 56.6 N.
5. Suppose that a student pulls with two large forces (F1 and F2)
in order to lift a 1-kg book by two cables. If the cables make a 1-degree angle
with the horizontal, then what is the tension in the cable?
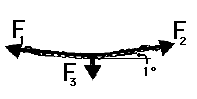
The tension 281 Newtons!
Since the mass is 1 kg, the weight is 9.8 N. Each cable must
pull upwards with 4.9 N of force. Thus,
sine (1 degree) = (4.9 N)
/ (Ftens).
Proper use of algebra leads to the equation
Ftens = (4.9 N) / [ sine (1 degree) ] = 281 N.