Forces in Two Dimensions
Addition
of Forces
We studied
the use of Newton's second law and free-body diagrams to determine the net
force and acceleration of objects. In that unit, the forces acting upon objects
were always directed in one dimension. There may have been both horizontal and
vertical forces acting upon objects; yet there were never individual forces
that were directed both horizontally and vertically. Furthermore, when a free-body diagram analysis was performed, the net force was either
horizontal or vertical; the net force (and corresponding acceleration) was never
both horizontal and vertical. Now times have changed and you are ready for
situations involving forces in two dimensions. In this unit, we will examine
the effect of forces acting at angles to the horizontal, such that the force
has an influence in two dimensions - horizontally and vertically. For such
situations, Newton's
second law applies as
it always did for situations involving one-dimensional net forces. However, to
use Newton's laws, common vector operations such as vector addition and vector
resolution will have to be applied. In this part of Lesson 3, the rules for adding vectors will be reviewed and applied to the addition
of force vectors.
Analyzing Three Forces to Determine the Net Force
Methods
of adding vectors were
discussed earlier in Lesson 1 of this unit. During that discussion, the head to tail method of vector addition was introduced as a useful method of adding
vectors that are not at right angles to each other. Now we will see how that
method applies to situations involving the addition of force vectors.
A force
board (or force table) is a common physics lab apparatus that has three (or
more) chains or cables attached to a center ring.
The chains or cables exert forces upon the center ring
in three different directions. Typically the experimenter adjusts the direction
of the three forces, makes measurements of the amount of force in each
direction, and determines the vector sum of three forces. Forces perpendicular
to the plane of the force board are typically ignored in the analysis.
Suppose
that a force board or a force table is used such that there are three forces
acting upon an object. (The object is the ring in the center of
the force board or force table.) In this situation, two of the forces are
acting in two-dimensions. A top view of these three forces could be represented by
the following diagram.
The
goal of a force analysis is to determine the net force and the corresponding
acceleration. The net forceis the
vector sum of all the forces. That is, the net force is the resultant of all
the forces; it is the result of adding all the forces together as vectors. For
the situation of the three forces on the force board, the net force is the sum
of force vectors A + B + C.
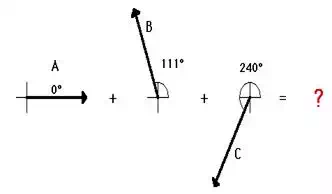
One
method of determining the vector sum of these three forces (i.e., the net
force") is to employ the method of head-to-tail addition. In this method,
an accurately drawn scaled diagram is used and each individual vector is drawn to scale. Where the head of one
vector ends, the tail of the next vector begins. Once all vectors are added,
the resultant (i.e., the vector sum) can be determined by
drawing a vector from the tail of the first vector to the head of the
last vector. This procedure is shown below. The three vectors are added using
the head-to-tail method. Incidentally, the vector sum of the three vectors is 0
Newton - the three vectors add up to 0 Newton. The last vector ends where the
first vector began such that there is no resultant vector.
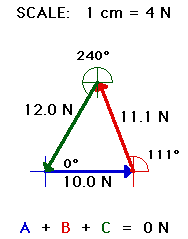
The
purpose of adding force vectors is to determine the net force acting upon an object. In the above case, the
net force (vector sum of all the forces) is 0 Newton. This would be expected
for the situation since the object (the ring in the center of
the force table) is at rest and staying at rest. We would say that the object
is at equilibrium. Any
object upon which all the forces are balanced (Fnet = 0 N) is said to be at equilibrium.
Quite
obviously, the net force is not always 0 Newton. In fact, whenever objects are
accelerating, the forces will not balance and the net force will be nonzero. This is consistent with Newton's first law of motion. For
example consider the situation described below.
An Example to Test Your
Understanding
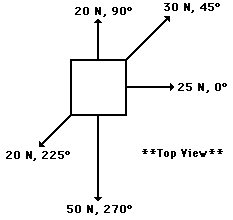A pack of
five Artic wolves are exerting five different forces upon the carcass of a
500-kg dead polar bear. A top view showing the magnitude and direction of each of
the five individual forces is shown in the diagram at the right. The counterclockwise convention is used to indicate the
direction of each force vector. Remember that this is a top view of the
situation and as such does not depict the gravitational and normal forces
(since they would be perpendicular to the plane of your computer monitor); it can
be assumed that the gravitational and normal forces balance each other. Use a
scaled vector diagram to determine the net force acting upon the polar bear.
Then compute the acceleration of the polar bear (both magnitude and direction).
When finished, check your answer by clicking the button and then view the
solution to the problem by analyzing the
diagrams shown below.
The net force is 39.4 N at 324 degrees.
The acceleration
of the polar bear is 0.0788 m/s/s. This value is found by dividing Fnet by
m (39.4 N) / (500 kg)
The
task of determining the vector sum of all the forces for the polar bear problem
involves constructing an accurately drawn scaled vector diagram in which all
five forces are added head-to-tail. The following five forces must be added.
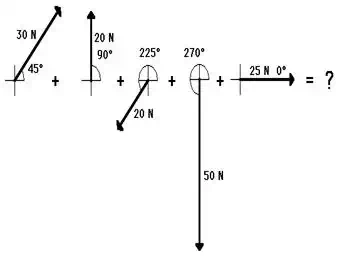
The
scaled vector diagram for this problem would look like the following:
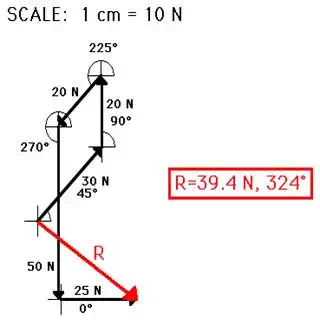
The
above two problems (the force table
problem and the polar bear problem) illustrate the use of the
head-to-tail method for determining the vector sum of all the forces. The
resultants in each of the above diagrams represent the net force acting upon
the object. This net force is related to the acceleration of the object. Thus,
to put the contents of this page in perspective with other material studied in
this course, vector addition methods can be utilized to determine the sum of
all the forces acting upon an object and subsequently the acceleration of that
object. And the acceleration of an object can be combined with kinematic
equations to determine motion information (i.e., the final velocity, the
distance traveled, etc.) for a given object.
Sometimes 10
+ 10 = 10
In
addition to knowing graphical methods of adding the forces acting upon an
object, it is also important to have a conceptual grasp of the principles of
adding forces. Let's begin by considering the addition of two forces, both
having a magnitude of 10 Newton. Suppose the question is posed:
10 Newton + 10 Newton = ???
How
would you answer such a question? Would you quickly conclude 20 Newton,
thinking that two force vectors can be added like any two numerical quantities?
Would you pause for a moment and think that the quantities to be added are
vectors (force vectors) and the addition of vectors follow a different set of
rules than the addition of scalars? Would you pause for a moment, pondering the
possible ways of adding 10 Newton and 10 Newton and conclude, "it depends upon their direction?" In fact, 10
Newton + 10 Newton could give almost any resultant, provided that it has a
magnitude between 0 Newton and 20 Newton. Study the diagram below in which 10
Newton and 10 Newton are added to give a variety of answers; each answer is
dependent upon the direction of the two vectors that are to be added. For this
example, the minimum magnitude for the resultant is 0 Newton (occurring when 10
N and 10 N are in the opposite direction); and the maximum magnitude for the
resultant is 20 N (occurring when 10 N and 10 N are in the same direction).
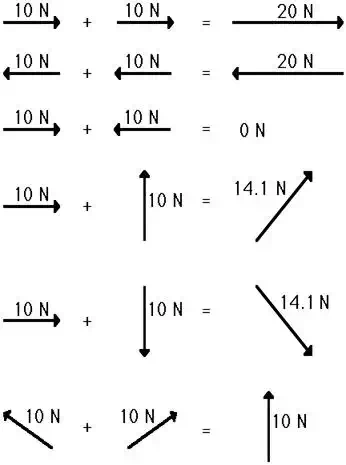
The
above diagram shows what is occasionally a difficult
concept to believe. Many students find it difficult to see how 10 N + 10
N could ever be equal to 10 N. For reasons to be discussed in the next section
of this lesson, 10 N + 10 N would equal 10 N whenever the two forces to be
added are at 30 degrees to the horizontal. For now, it ought to be sufficient
to merely show a simple vector addition diagram for the addition of the two forces
(see diagram below).
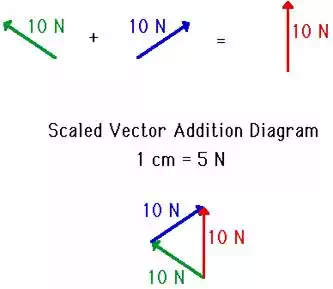
Check Your Understanding
Answer
the following questions and then view the answers by clicking on the button.
1.
Barb Dwyer recently submitted her vector addition homework assignment. As seen
below, Barb added two vectors and drew the resultant. However, Barb Dwyer
failed to label the resultant on the diagram. For each case, that is the
resultant (A, B, or C)? Explain.
Diagram A: A is the resultant of B + C. Barb added B + C using the head-to-tail method and then drew
the resultant from the tail of the first vector (B) to the head of the last
vector (C).
Diagram B: A is the resultant of C + B. Barb added B + C using
the head-to-tail method a and then drew the
resultant from the tail of the first vector (C) to the head of the last vector
(B).
2.
Consider the following five force vectors.
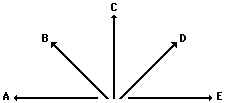
Sketch
the following and draw the resultant (R). Do not draw a scaled vector diagram;
merely make a sketch. Label each vector. Clearly label the resultant (R).
A + C + D
B + E + D
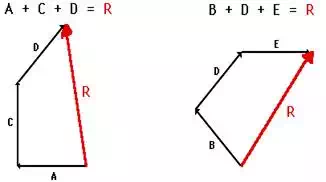
3.
On two different occasions during a high school soccer game, the ball was
kicked simultaneously by players on opposing teams. In which case (Case 1 or
Case 2) does the ball undergo the greatest acceleration? Explain your answer.
Case 2 results in the greatest
acceleration. Even though the individual forces are greater in Case 1, the net
force is greatest in Case 2. Acceleration depends on the net force; it is not
dependent on the size of the individual forces.
close
4.
Billie Budten and Mia Neezhirt are having an intense argument at the lunch
table. They are adding two force vectors together to determine the resultant
force. The magnitude of the two forces are 3 N and 4 N. Billie is arguing that
the sum of the two forces is 7 N. Mia argues that the two forces add together
to equal 5 N. Who is right? Explain.
Both Billie and
Mia could be right. Yet with the lack of information about the direction of the two
vectors, it is impossible to tell who is right. The only conclusion that we can
make is that the sum of the two vectors is no greater than 7 N (if the two
vectors were directed in the same direction) and no smaller than 1 N (if the
two vectors were directed in opposite directions).
close
5.
Matt Erznott entered the classroom for his
physics class. He quickly became amazed by the remains of some of teacher's
whiteboard scribblings. Evidently, the teacher had taught his class on that day
that
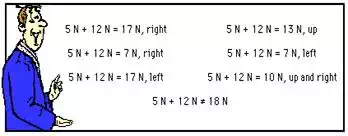
Explain
why the equalities are indeed equalities and the inequality must definitely be
an inequality.
Depending on the
direction of the 5 N and 12 N forces, the magnitude of the sum could be as big
as 17 N (obtained when the two forces are in the same direction) and as small
as 7 N (obtained when the two forces are in opposite directions). However, the
sum of 5 N and 12 N could never be 18 N.