Describing Projectiles With Numbers: (Horizontal and Vertical Displacement)

The previous diagrams, tables, and discussion pertain to how the horizontal and vertical components of the velocity vector change with time during the course of projectile's trajectory. Now we will investigate the manner in which the horizontal and vertical components of a projectile's displacement vary with time.As has already been discussed, the vertical displacement (denoted by the symbol y in the discussion below) of a projectile is dependent only upon the acceleration of gravity and not dependent upon the horizontal velocity. Thus, the vertical displacement (y) of a projectile can be predicted using the same equation used to find the displacement of a free-falling object undergoing one-dimensional motion. This equation was discussed in Unit 1 of The Physics Classroom. The equation can be written as follows.

y = 0.5 • g • t²

(equation for vertical displacement for a horizontally launched projectile)

where g is -9.8 m/s/s and t is the time in seconds. The above equation pertains to a projectile with no initial vertical velocity and as such predicts the vertical distance that a projectile falls if dropped from rest. It was also discussed earlier, that the force of gravity does not influence the horizontal motion of a projectile. The horizontal displacement of a projectile is only influenced by the speed at which it moves horizontally (v_ix) and the amount of time (t) that it has been moving horizontally. Thus, if the horizontal displacement (x) of a projectile were represented by an equation, then that equation would be written as

x = v_ix • t

The diagram below shows the trajectory of a projectile (in red), the path of a projectile released from rest with no horizontal velocity (in blue) and the path of the same object when gravity is turned off (in green). The position of the object at 1-second intervals is shown. In this example, the initial horizontal velocity is 20 m/s and there is no initial vertical velocity (i.e., a case of a horizontally launched projectile).

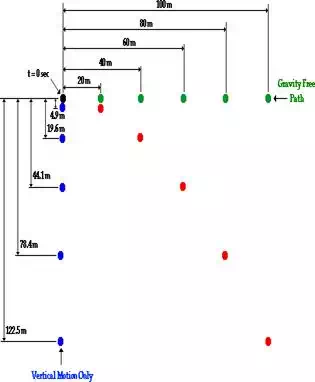
As can be seen in the diagram above, the vertical distance fallen from rest during each consecutive second is increasing (i.e., there is a vertical acceleration). It can also be seen that the vertical displacement follows the equation above (y = 0.5 • g • t²). Furthermore, since there is no horizontal acceleration, the horizontal distance traveled by the projectile each second is a constant value - the projectile travels a horizontal distance of 20 meters each second. This is consistent with the initial horizontal velocity of 20 m/s. Thus, the horizontal displacement is 20 m at 1 second, 40 meters at 2 seconds, 60 meters at 3 seconds, etc. This information is summarized in the table below.

Time	Horizontal Displacement	Vertical Displacement
0 s	0 m	0 m
1 s	20 m	-4.9 m
2 s	40 m	-19.6 m
3 s	60 m	-44.1 m
4 s	80m	-78.4 m
5 s	100 m	-122.5 m

Now consider displacement values for a projectile launched at an angle to the horizontal (i.e., a non-horizontally launched projectile). How will the presence of an initial vertical component of velocity affect the values for the displacement? The diagram below depicts the position of a projectile launched at an angle to the horizontal. The projectile still falls 4.9 m, 19.6 m, 44.1 m, and 78.4 m below the straight-line, gravity-free path. These distances are indicated on the diagram below.

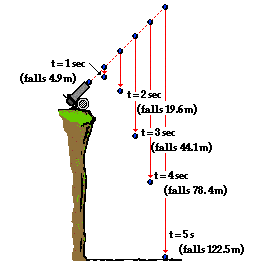
The projectile still falls below its gravity-free path by a vertical distance of 0.5*g*t^2. However, the gravity-free path is no longer a horizontal line since the projectile is not launched horizontally. In the absence of gravity, a projectile would rise a vertical distance equivalent to the time multiplied by the vertical component of the initial velocity (v_iy• t). In the presence of gravity, it will fall a distance of 0.5 • g • t². Combining these two influences upon the vertical displacement yields the following equation.

y = v_iy • t + 0.5 • g • t²

(Equation for vertical displacement for an angled-launched projectile)

where v_iy is the initial vertical velocity in m/s, t is the time in seconds, and g = -9.8 m/s/s (an approximate value of the acceleration of gravity). If a projectile is launched with an initial vertical velocity of 19.6 m/s and an initial horizontal velocity of 33.9 m/s, then the x- and y- displacements of the projectile can be calculated using the equations above. A sample calculation is shown below.

Calculations for t = 1 second

y = viy * t + 0.5*g*t^2 where viy = 19.6 m/s y = (19.6 m/s) * (1 s) + 0.5*(-9.8 m/s/s)*(1 s)^2 y = 19.6 m + (-4.9 m) y = 14.7 m (approximately)

x = vix * t where vix = 33.9 m/s x = (33.9 m/s) * (1 s) x = 33.9 m

The following table lists the results of such calculations for the first four seconds of the projectile's motion.

Time	Horizontal Displacement	Vertical Displacement
0 s	0 m	0 m
1 s	33.9 m	14.7 m
2 s	67.8 m	19.6 m
3 s	101.7 m	14.7 m
4 s	135.6 m	0 m

The data in the table above show the symmetrical nature of a projectile's trajectory. The vertical displacement of a projectile t seconds before reaching the peak is the same as the vertical displacement of a projectile t seconds after reaching the peak. For example, the projectile reaches its peak at a time of 2 seconds; the vertical displacement is the same at 1 second (1 s before reaching the peak) is the same as it is at 3 seconds (1 s after reaching its peak). Furthermore, the time to reach the peak (2 seconds) is the same as the time to fall from its peak (2 seconds).

Check Your Understanding

Use your understanding of projectiles to answer the following questions. Then click the button to view the answers.

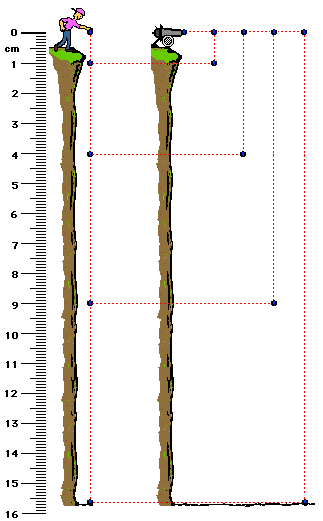
1. Anna Litical drops a ball from rest from the top of 78.4-meter high cliff. How much time will it take for the ball to reach the ground and at what height will the ball be after each second of motion?

See Answer

It will take 4 seconds to fall 78.4 meters

Use the equation y = 0.5 • g • t² and substitute -9.8 m/s/s for g. The vertical displacement must then be subtracted from the initial height of 78. 4 m.

At t = 1 s, y = 4.9 m (down) so height is 73.5 m (78.4 m - 4.9 m )

At t = 2 s, y = 19.6 m (down) so height is 58.8 m (78.4 m - 19.6 m )

At t = 3 s, y = 44.1 m (down) so height is 34.3 m (78.4 m - 45 m)

At t = 4 s, y = 78.4 m (down) so height is 0 m (78.4 m - 78.4 m)

2. A cannonball is launched horizontally from the top of an 78.4-meter high cliff. How much time will it take for the ball to reach the ground and at what height will the ball be after each second of travel?

See Answer

It will still take 4 seconds to fall 78.4 meters

Use the equation y = 0.5 • g • t² and substitute -9.8 m/s/s for g. The vertical displacement must then be subtracted from the initial height of 78. 4 m.

At t = 1 s, y = 4.9 m (down) so height is 73.5 m (78.4 m - 4.9 m )

At t = 2 s, y = 19.6 m (down) so height is 58.8 m (78.4 m - 19.6 m )

At t = 3 s, y = 44.1 m (down) so height is 34.3 m (78.4 m - 45 m)

At t = 4 s, y = 78.4 m (down) so height is 0 m (78.4 m - 78.4 m)

NOTE: the cannon ball's horizontal speed does not affect the time to fall a vertical distance of 78.4 m.

3. Fill in the table below indicating the value of the horizontal and vertical components of velocity and acceleration for a projectile.

See Answer

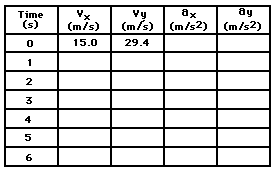
The v_x values will remain constant at 15.0 m/s for the entire 6 seconds; the a_x values will be 0 m/s/s for the entire 6 seconds.

The v_y values will be changing by -9.8 m/s each second. Thus,

v_y = 29.4 m/s (t = 0 s)

v_y = 19.6 m/s (t = 1 s)

v_y = 9.8 m/s (t = 2 s)

v_y = 0 m/s (t = 3 s)

v_y = -9.8 m/s (t = 4 s)

v_y = -19.6 m/s (t = 5 s)

v_y = -29.4 m/s (t = 6 s)

The a_y values will be -9.8 m/s/s for the entire 6 seconds.

4. The diagram below shows the trajectory for a projectile launched non-horizontally from an elevated position on top of a cliff. The initial horizontal and vertical components of the velocity are 8 m/s and 19.6 m/s respectively. Positions of the object at 1-second intervals are shown. Determine the horizontal and vertical velocities at each instant shown in the diagram.

See Answer

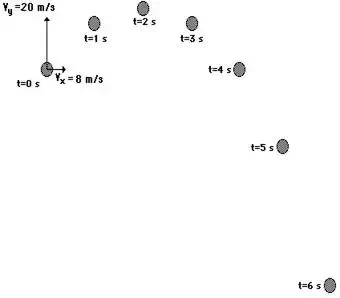
The v_x values will remain 8 m/s for the entire 6 seconds.

The v_y values will be changing by 9.8 m/s each second. Thus,

v_y =9.8 m/s (t = 1 s)

v_y = 0 m/s (t = 2 s)

v_y = -9.8 m/s (t = 3 s)

v_y = -19.6 m/s (t = 4 s)

v_y = -29.4 m/s (t = 5 s)

v_y = -39.2 m/s (t = 6 s)

The following diagram pertains to questions #1 and #2 above. A scale is used where 1 cm = 5 meters. (Note that 1-cm may be a different distance for different computer monitors; thus, a cm-ruler is given in the diagram.)