Characteristics of a Projectile's Trajectory

As discussed earlier in this lesson, a projectile is an object upon which the only force acting is gravity. Many projectiles not only undergo a vertical motion, but also undergo a horizontal motion. That is, as they move upward or downward they are also moving horizontally. There are the two components of the projectile's motion - horizontal and vertical motion. And since perpendicular components of motion are independent of each other, these two components of motion can (and must) be discussed separately. The goal of this part of the lesson is to discuss the horizontal and vertical components of a projectile's motion; specific attention will be given to the presence/absence of forces, accelerations, and velocity.

Horizontally Launched Projectiles

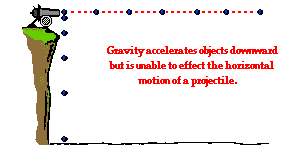Let's return to our thought experiment from earlier in this lesson. Consider a cannonball projected horizontally by a cannon from the top of a very high cliff. In the absence of gravity, the cannonball would continue its horizontal motion at a constant velocity. This is consistent with the law of inertia. And furthermore, if merely dropped from rest in the presence of gravity, the cannonball would accelerate downward, gaining speed at a rate of 9.8 m/s every second. This is consistent with our conception of free-falling objects accelerating at a rate known as the acceleration of gravity.

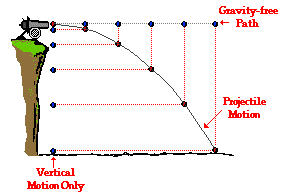
If our thought experiment continues and we project the cannonball horizontally in the presence of gravity, then the cannonball would maintain the same horizontal motion as before - a constant horizontal velocity. Furthermore, the force of gravity will act upon the cannonball to cause the same vertical motion as before - a downward acceleration. The cannonball falls the same amount of distance as it did when it was merely dropped from rest (refer to diagram below). However, the presence of gravity does not affect the horizontal motion of the projectile. The force of gravity acts downward and is unable to alter the horizontal motion. There must be a horizontal force to cause a horizontal acceleration. (And we know thatthere is only a vertical force acting upon projectiles.) The vertical force acts perpendicular to the horizontal motion and will not affect it since perpendicular components of motion are independent of each other. Thus, the projectile travels with a constant horizontal velocity and a downward vertical acceleration.

The above information can be summarized by the following table.

	Horizontal Motion	Vertical Motion
Forces (Present? - Yes or No) (If present, what dir'n?)	No	Yes The force of gravity acts downward
Acceleration (Present? - Yes or No) (If present, what dir'n?)	No	Yes "g" is downward at 9.8 m/s/s
Velocity (Constant or Changing?)	Constant	Changing (by 9.8 m/s each second)

Non-Horizontally Launched Projectiles

Now suppose that our cannon is aimed upward and shot at an angle to the horizontal from the same cliff. In the absence of gravity (i.e., supposing that the gravity switch could be turned off) the projectile would again travel along a straight-line, inertial path. An object in motion would continue in motion at a constant speed in the same direction if there is no unbalanced force. This is the case for an object moving through space in the absence of gravity. However, if the gravity switchcould be turned on such that the cannonball is truly a projectile, then the object would once more free-fall below this straight-line, inertial path. In fact, the projectile would travel with a parabolic trajectory. The downward force of gravity would act upon the cannonball to cause the same vertical motion as before - a downward acceleration. The cannonball falls the same amount of distance in every second as it did when it was merely dropped from rest (refer to diagram below). Once more, the presence of gravity does not affect the horizontal motion of the projectile. The projectile still moves the same horizontal distance in each second of travel as it did when the gravity switch was turned off. The force of gravity is a vertical force and does not affect horizontal motion; perpendicular components of motion are independent of each other.

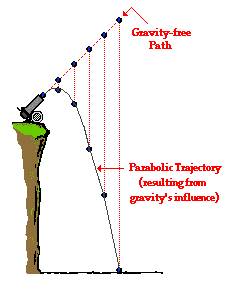
In conclusion, projectiles travel with a parabolic trajectory due to the fact that the downward force of gravity accelerates them downward from their otherwise straight-line, gravity-free trajectory. This downward force and acceleration results in a downward displacement from the position that the object would be if there were no gravity. The force of gravity does not affect the horizontal component of motion; a projectile maintains a constant horizontal velocity since there are no horizontal forces acting upon it.

Check Your Understanding

Use your understanding of projectiles to answer the following questions. When finished, click the button to view your answers.

1. Consider these diagrams in answering the following questions.

Which diagram (if any) might represent ...

a. ... the initial horizontal velocity?

b. ... the initial vertical velocity?

c. ... the horizontal acceleration?

d. ... the vertical acceleration?

e. ... the net force?

See Answer

a. The initial horizontal velocity is A (It's the only horizontal vector).

b. The initial vertical velocity could be B (if projected down) or C (if projected upward).

c. None of these; there is no horizontal acceleration.

d. The vertical acceleration is B; it is always downwards.

e. The net force on a projectile is B (there is only one force - gravity; and it is downwards).

2. Supposing a snowmobile is equipped with a flare launcher that is capable of launching a sphere vertically (relative to the snowmobile). If the snowmobile is in motion and launches the flare and maintains a constant horizontal velocity after the launch, then where will the flare land (neglect air resistance)?

a. in front of the snowmobile

b. behind the snowmobile

c. in the snowmobile

See Answer

The answer is C.

The flare will land in the snowmobile.

The horizontal motion of the falling flare remains constant, and as such, the flare will always be positioned directly above the snowmobile. The force of gravity causes the flare to slow down and then return to the ground; yet it does not affect the horizontal motion of the flare.

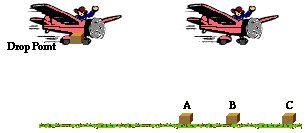3. Suppose a rescue airplane drops a relief package while it is moving with a constant horizontal speed at an elevated height. Assuming that air resistance is negligible, where will the relief package land relative to the plane?

a. below the plane and behind it.

b. directly below the plane

c. below the plane and ahead of it

See Answer

The answer is B.

The package will land directly below the plane. The horizontal motion of the falling package remains constant, and as such, the package will always be positioned directly below the plane. The force of gravity causes the package to fall but does not affect its horizontal motion.