Component Method of Vector Addition

·          

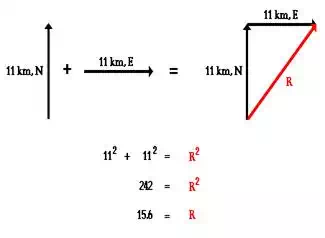
Earlier in this lesson, we learned that vectors oriented at right angles to one another can be added together using the Pythagorean theorem. For instance, two displacement vectors with magnitude and direction of 11 km, North and 11 km, East can be added together to produce a resultant vector that is directed both north and east. When the two vectors are added head-to-tail as shown below, the resultant is the hypotenuse of a right triangle. The sides of the right triangle have lengths of 11 km and 11 km. The resultant can be determined using the Pythagorean theorem; it has a magnitude of 15.6 km. The solution is shown below the diagram.

http://www.physicsclassroom.com/Class/vectors/u3l1b3.webp


This Pythagorean approach is a useful approach for adding any two vectors that are directed at right angles to one another. A right triangle has two sides plus a hypotenuse; so the Pythagorean Theorem is perfect for adding two right angle vectors. But there are limits to the usefulness of the Pythagorean Theorem in solving vector addition problems. For instance, the addition of three or four vectors does not lead to the formation of a right triangle with two sides and a hypotenuse. So at first glance it may seem that it is impossible to use the Pythagorean Theorem to determine the resultant for the addition of three or four vectors. Furthermore, the Pythagorean Theorem works when the two added vectors are at right angles to one another - such as for adding a north vector and an east vector. But what can one do if the two vectors that are being added are not at right angles to one another? Is there a means of using mathematics to reliably determine the resultant for such vector addition situations? Or is the student of physics left to determining such resultants using a scaled vector diagram? Here on this page, we will learn how to approach more complex vector addition situations by combining the concept of vector components (discussed earlier) and the principles of vector resolution (discussed earlier) with the use of the Pythagorean theorem (discussed earlier).