Trigonometric Method of Vector Resolution

The trigonometric method of vector resolution involves using trigonometric functions to determine the components of the vector. Earlier in lesson 1, the use of trigonometric functions to determine the direction of a vector was described. Now in this part of lesson 1, trigonometric functions will be used to determine the components of a single vector. Recall from the earlier discussion that trigonometric functions relate the ratio of the lengths of the sides of a right triangle to the measure of an acute angle within the right triangle. As such, trigonometric functions can be used to determine the length of the sides of a right triangle if an angle measure and the length of one side are known.

The method of employing trigonometric functions to determine the components of a vector are as follows:

1. Construct a rough sketch (no scale needed) of the vector in the indicated direction. Label its magnitude and the angle that it makes with the horizontal.

2. Draw a rectangle about the vector such that the vector is the diagonal of the rectangle. Beginning at the tail of the vector, sketch vertical and horizontal lines. Then sketch horizontal and vertical lines at the head of the vector. The sketched lines will meet to form a rectangle.

3. Draw the components of the vector. The components are the sides of the rectangle. The tail of each component begins at the tail of the vector and stretches along the axes to the nearest corner of the rectangle. Be sure to place arrowheads on these components to indicate their direction (up, down, left, right).

4. Meaningfully label the components of the vectors with symbols to indicate which component represents which side. A northward force component might be labeled F_north. A rightward force velocity component might be labeled v_x; etc.

5. To determine the length of the side opposite the indicated angle, use the sine function. Substitute the magnitude of the vector for the length of the hypotenuse. Use some algebra to solve the equation for the length of the side opposite the indicated angle.

6. Repeat the above step using the cosine function to determine the length of the side adjacent to the indicated angle.

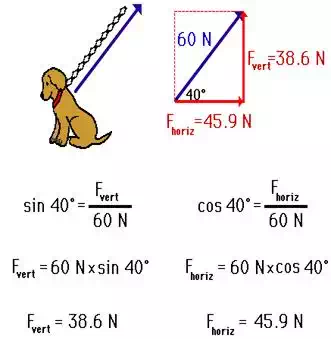
The above method is illustrated below for determining the components of the force acting upon Fido. As the 60-Newton tension force acts upward and rightward on Fido at an angle of 40 degrees, the components of this force can be determined using trigonometric functions.