Using Trigonometry to Determine a Vector's Direction

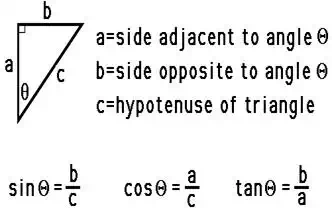
The direction of a resultant vector can often be determined by use of trigonometric functions. Most students recall the meaning of the useful mnemonic SOH CAH TOA from their course in trigonometry. SOH CAH TOA is a mnemonic that helps one remember the meaning of the three common trigonometric functions - sine, cosine, and tangent functions. These three functions relate an acute angle in a right triangle to the ratio of the lengths of two of the sides of the right triangle. The sine function relates the measure of an acute angle to the ratio of the length of the side opposite the angle to the length of the hypotenuse. The cosine function relates the measure of an acute angle to the ratio of the length of the side adjacent the angle to the length of the hypotenuse. The tangent function relates the measure of an angle to the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle. The three equations below summarize these three functions in equation form.

These three trigonometric functions can be applied to the hiker problem in order to determine the direction of the hiker's overall displacement. The process begins by the selection of one of the two angles (other than the right angle) of the triangle. Once the angle is selected, any of the three functions can be used to find the measure of the angle. Write the function and proceed with the proper algebraic steps to solve for the measure of the angle. The work is shown below.

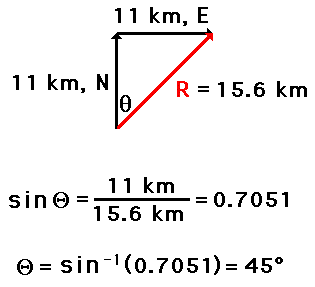
Once the measure of the angle is determined, the direction of the vector can be found. In this case the vector makes an angle of 45 degrees with due East. Thus, the direction of this vector is written as 45 degrees. (Recall from earlier in this lesson that the direction of a vector is the counterclockwise angle of rotation that the vector makes with due East.)