Vector Addition

A variety of mathematical operations can be performed with and upon vectors. One such operation is the addition of vectors. Two vectors can be added together to determine the result (or resultant). This process of adding two or more vectors has already been discussed in an earlier unit. Recall in our discussion of Newton's laws of motion, that the net force experienced by an object was determined by computing the vector sum of all the individual forces acting upon that object. That is the net force was the result (or resultant) of adding up all the force vectors. During that unit, the rules for summing vectors (such as force vectors) were kept relatively simple. Observe the following summations of two force vectors:

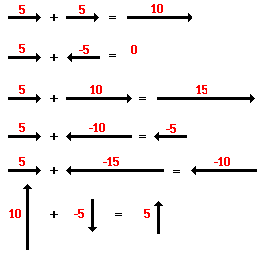
These rules for summing vectors were applied to free-body diagrams in order to determine the net force (i.e., the vector sum of all the individual forces). Sample applications are shown in the diagram below.

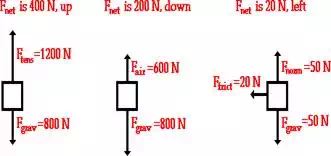
In this unit, the task of summing vectors will be extended to more complicated cases in which the vectors are directed in directions other than purely vertical and horizontal directions. For example, a vector directed up and to the right will be added to a vector directed up and to the left. The vector sum will be determined for the more complicated cases shown in the diagrams below.

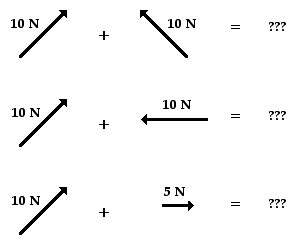
There are a variety of methods for determining the magnitude and direction of the result of adding two or more vectors. The two methods that will be discussed in this lesson and used throughout the entire unit are:

· the Pythagorean theorem and trigonometric methods

· the head-to-tail method using a scaled vector diagram