Double Trouble (a.k.a., Two Body Problems)

Our study thus far has been restricted to the analysis of single objects moving under the influence of Newton's laws. But what happens if there are two objects connected together in one way or another? For instance, there could be a tow truck hauling a car down a highway. How is such an analysis conducted? How is the acceleration of the tow truck and the car determined? What about the force acting between the tow truck and the car? In this part of Lesson 3, we will make an attempt to analyze such situations. We will find that the analysis is conducted in the same general manner as when there is one object - through the use of free-body diagrams and Newton's laws.

The Basic Approach

Situations involving two objects are often referred to as two-body situations. When appearing as physics problems, two-body problems are characterized by a set of two unknown quantities. Most commonly (though not always the case), the two unknowns are the acceleration of the two objects and the force transmitted between the two objects. Two body-problems can typically be approached using one of two basic approaches. One approach involves a combination of a system analysis and an individual body analysis. In the system analysis, the two objects are considered to be a single object moving (or accelerating) together as a whole. The mass of the system is the sum of the mass of the two individual objects. If acceleration is involved, the acceleration of the system is the same as that of the individual objects. A system analysis is usually performed to determine the acceleration of the system. The system analysis is combined with an individual object analysis. In the individual object analysis, either one of the two objects is isolated and considered as a separate, independent object. A free-body diagram is constructed and the individual forces acting upon the object are identified and calculated. An individual object analysis is usually performed in order to determine the value of any force which acts between the two objects - for example, contact forces or tension forces.

The dual combination of a system analysis and an individual object analysis is one of two approaches that are typically used to analyze two-body problems. A second approach involves the use of two separate individual object analyses. In such an approach, free-body diagrams are constructed independently for each object and Newton's second law is used to relate the individual force values to the mass and acceleration. Each individual object analysis generates an equation with an unknown. The result is a system of two equations with two unknowns. The system of equations is solved in order to determine the unknown values.

As a first example of the two approaches to solving two-body problems, consider the following example problem.

Example Problem 1:

A 5.0-kg and a 10.0-kg box are touching each other. A 45.0-N horizontal force is applied to the 5.0-kg box in order to accelerate both boxes across the floor. Ignore friction forces and determine the acceleration of the boxes and the force acting between the boxes.

The first approach to this problem involves the dual combination of a system analysis and an individual object analysis. As mentioned, the system analysis is used to determine the acceleration and the individual object analysis is used to determine the forces acting between the objects. In the system analysis, the two objects are considered 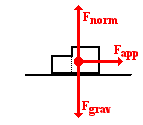to be a single object. The dividing line that separates the objects is ignored. The mass of the system of two objects is 15.0 kg. The free-body diagram for the system is shown at the right. There are three forces acting upon the system - the gravity force (the Earth pulls down on the 15.0 kg of mass), the normal force (the floor pushes up on the system to support its weight), and the applied force (the hand is pushing on the back part of the system). The force acting between the 5.0-kg box and the 10.0-kg box is not considered in the system analysis since it is an internal force. Just as the forces holding atoms together within an object are not included in a free-body diagram, so the forces holding together the parts of a system are ignored. These are considered internal forces; only external forces are considered when drawing free-body diagrams. The magnitude of the force of gravity is m•g or 147 N. The magnitude of the normal force is also 147 N since it must support the weight (147 N) of the system. The applied force is stated to be 45.0 N. Newton's second law (a = F_net/m) can be used to determine the acceleration. Using 45.0 N for F_net and 15.0 kg for m, the acceleration is 3.0 m/s².

Now that the acceleration has been determined, an individual object analysis can be performed on either object in order to determine the force acting between them. It does not matter which object is chosen; the result will be the same in either case. Here the individual object analysis is conducted on the 10.0 kg object (only because there is one less force acting on it). The free-body diagram for the 10.0-kg object is shown at the right. There are only three forces acting upon it - the force of gravity on the 10.0-kg, the support force (from the floor pushing upward) and the rightward contact force (F_contact). As the 5.0-kg object accelerates to the right, it will be pushing rightward upon the 10.0-kg object; this is known as a contact force (or a normal force or an applied force or …). The vertical forces balance each other since there is no vertical acceleration. The only unbalanced force on the 10.0-kg object is the Fcontact. This force is the net force and is equal to m•a where m is equal to 10.0 kg (since this analysis is for the 10.0-kg object) and a was already determined to be 3.0 m/s². The net force is equal to 30.0 N. This net force is the force of the 5.0-kg object pushing the 10.0-kg object to the right; it has a magnitude of 30.0 N. So the answers to the two unknowns for this problem are 3.0 m/s² and 30.0 N.

Now we will consider the solution to this same problem using the second approach - the use of two individual object analyses. In the process of this second approach, we will ignore the fact that we know what the answers are and presume that we are solving the problem for the first time. In this approach, two separate free-body diagram analyses are performed. The diagrams below show the free-body diagrams for the two objects.

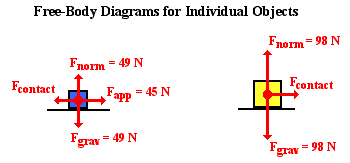
Note that there are four forces on the 5.0-kg object at the rear. The two vertical forces - F_grav and F_norm - are obvious forces. The 45.0-N applied force (F_app) is the result of the hand pushing on the rear object as described in the problem statement and depicted in the diagram. The leftward contact force on the 5.0-kg object is the force of the 10.0-kg object pushing leftward on the 5.0-kg object. As an attempt is made to push the rear object (5.0-kg object) forward, the front object (10.0-kg object) pushes back upon it. This force is equal to and opposite of the rear object pushing forward on the front object. This force is simply labeled as F_contact for both of the free-body diagrams. In the free-body diagram for the 10.0-kg object, there are only three forces. Once more, the two vertical forces - F_grav and F_norm - are obvious forces. The horizontal force is simply the 5.0-kg object pushing the 10.0-kg object forward. The 45.0 N applied force is not exerted upon this 10.0-kg object; it is exerted on the 5.0-kg object and has already been considered in the previous free-body diagram.

Now the goal of this approach is to generate system of two equations capable of solving for the two unknown values. Using F_net = m•a with the free-body diagram for the 5.0-kg object will yield the Equation 1 below:

45.0 - F_contact = 5.0•a

Using F_net = m•a with the free-body diagram for the 10.0-kg object will yield the Equation 2 below:

F_contact = 10.0•a

(Note that the units have been dropped from Equations 1 and 2 in order to clean the equations up.) If the expression 10.0•a is substituted into Equation 1 for F_contact, then Equation 1 becomes reduced to a single equation with a single unknown. The equation becomes

45.0 - 10.0•a = 5.0•a

A couple of steps of algebra lead to an acceleration value of 3.0 m/s². This value of a can be substituted back into Equation 2 in order to determine the contact force:

F_contact = 10.0•a = 10.0 •3.0
F_contact = 30.0 N

As can be seen, using the second approach to solve two body problems yields the same two answers for the two unknowns. Now we will try the same two approaches on a very similar problem that includes a friction force.

Example Problem 2:

A 5.0-kg and a 10.0-kg box are touching each other. A 45.0-N horizontal force is applied to the 5.0-kg box in order to accelerate both boxes across the floor. The coefficient of kinetic friction is 0.200. Determine the acceleration and the contact force.

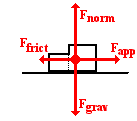Our first solution to this problem will involve the dual combination of a system analysis and an individual object analysis. As you likely noticed, Example Problem 2 is similar to Example Problem 1 with the exception that the surface is not frictionless in Example Problem 2. So when conducting the system analysis in this second example, the friction on the 15-kg system must be considered. So the free-body diagram for the system now includes four forces - the same three as in Example Problem 1 plus a leftward force of friction. The force of friction on the system can be calculated as μ•F_norm where F_normis the normal force experienced by the system. The F_norm of the system is equal to the force of gravity acting upon the 15.0-kg system; this value is 147 N. So

F_frict = μ•F_norm = (0.200)•(147 N) = 29.4 N

The vertical forces balance each other - consistent with the fact that there is no vertical acceleration. The horizontal forces do not balance each other. The net force can be determined as the vector sum of F_app and F_frict. That is, F_net = 45.0 N, right + 29.4 N, left; these add to 15.6 N, right. The acceleration can now be calculated using Newton's second law.

a = F_net / m = (15.6 N/15.0 kg) = 1.04 m/s²

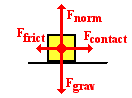Now that the system analysis has been used to determine the acceleration, an individual object analysis can be performed on either object in order to determine the force acting between them. Once more, it does not matter which object is chosen; the result would be the same in either case. The 10.0-kg object is chosen for the individual object analysis because there is one less force acting upon it; this makes the solution easier. There are four forces acting upon the 10.0-kg object. The two vertical forces are obvious - the force of gravity (98.0 N) and the normal force (equal to the force of gravity). The horizontal forces are the friction force to the left and the force of the 5.0-kg object pushing the 10.0-kg object forward; this is labeled as F_contact on the free-body diagram. The net force - vector sum of all the forces - can always be found by adding the forces in the direction of the acceleration and subtracting those that are in the opposite direction. This F_net is equal to F_contact - F_frict. Applying Newton's second law to this object yields the equation:

F_contact - F_frict = (10.0 kg)•(1.04 m/s²)

The friction force on this 10.0-kg object is not the same as the friction force on the system (since the system was weightier). The F_frict value can be computed as μ•F_norm where F_norm is the normal force experienced by the 10.0-kg object. The F_normof the 10.0-kg is equal to the force of gravity acting upon the 10.0-kg object; this value is 98.0 N. So

F_frict = μ•F_norm = (0.200)•(98.0 N) = 19.6 N

So now the value of 19.6 N can be substituted into the above equation and F_contact can be calculated:

F_contact - 19.6 N = (10.0 kg)•(1.04 m/s²)
F_contact = (10.0 kg)•(1.04 m/s²) + 19.6 N
F_contact = 30.0 N

So using the dual combination of the system analysis and individual body analysis allows us to determine the two unknown values - 1.04 m/s² for the acceleration and 30.0 N for the F_contact. Now we will see how two individual object analyses can be combined to generate a system of two equations capable of solving for the two unknowns. Once more we will start the analysis by presuming that we are solving the problem for the first time and do not know the acceleration nor the contact force. The free-body diagrams for the individual objects are shown below.

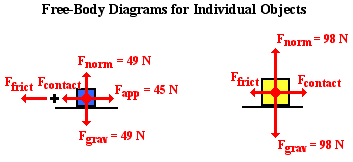
There are now five forces on the 5.0-kg object at the rear. The two vertical forces - F_grav and F_norm - are obvious forces. The 45.0-N applied force (F_app) is the result of the hand pushing on the rear object. The leftward contact force on the 5.0-kg object is the force of the 10.0-kg object pushing leftward on the 5.0-kg object. Its value is the same as the contact force that is exerted on the front 10.0-kg object by the rear 5.0-kg object. This force is simply labeled as F_contact for both of the free-body diagrams. Finally, the leftward friction force is the result of friction with the floor over which the 5.0-kg object moves. In the free-body diagram for the 10.0-kg object, there are now four forces. The two vertical forces - F_grav and F_norm - are obvious. The rightward contact force (F_contact) is simply the 5.0-kg object pushing the 10.0-kg object forward. And the leftward friction force is the result of friction with the floor. Once more, the 45.0 N applied force is not exerted upon this 10.0-kg object; it is exerted on the 5.0-kg object and has already been considered in the previous free-body diagram. The friction force for each object can be determined as μ•Fnorm where F_norm is the normal force experienced by the individual objects. Each object experiences a normal force equal to its weight (since vertical forces must balance). So the friction forces for the 5.0-kg object (49.0 N weight) and 10.0-kg object (98.0 N weight) are 0.200•49.0 N and 0.200•98.0 N, respectively.

Using these F_frict values and Newton's second law, a system of two equations capable of solving for the two unknown values can be written. Using F_net = m•a with the free-body diagram for the 5.0-kg object will yield Equation 3 below:

45.0 - F_contact - 9.8 = 5.0•a

Using F_net = m•a with the free-body diagram for the 10.0-kg object will yield the Equation 4 below:

F_contact - 19.6 = 10.0•a

(Note that the units have been dropped from Equations 3 and 4 in order to clean the equations up.) From Equation 4, F_contact = 10.0•a + 19.6. Substituting this expression for F_contact into Equation 3 and performing proper algebraic manipulations yields the acceleration value:

45.0 - (10.0•a + 19.6) - 9.8 = 5.0•a
45.0 - 19.6 - 9.8 = 15.0•a
15.6 = 15.0•a
a = (15.6/15.0)= 1.04 m/s²

This acceleration value can be substituted back into the expression for F_contact in order to determine the contact force:

F_contact = 10.0•a + 19.6 = 10.0•(1.04) + 19.6
F_contact = 30.0 N

Again we find that the second approach of using two individual object analyses yields the same set of answers for the two unknowns. The final example problem will involve a vertical motion. The approaches will remain the same.

Example Problem 3:

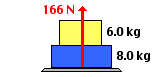A man enters an elevator holding two boxes - one on top of the other. The top box has a mass of 6.0 kg and the bottom box has a mass of 8.0 kg. The man sets the two boxes on a metric scale sitting on the floor. When accelerating upward from rest, the man observes that the scale reads a value of 166 N; this is the upward force upon the bottom box. Determine the acceleration of the elevator (and boxes) and determine the forces acting between the boxes.

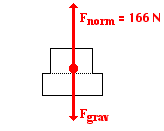Both approaches will be used to solve this problem. The first approach involves the dual combination of a system analysis and an individual object analysis. For the system analysis, the two boxes are considered to be a single system with a mass of 14.0 kg. There are two forces acting upon this system - the force of gravity and the normal force. The free-body diagram is shown at the right. The force of gravity is calculated in the usual manner using 14.0 kg as the mass.

F_grav = m•g = 14.0 kg • 9.8 N/kg = 137.2 N

Since there is a vertical acceleration, the vertical forces will not be balanced; the F_grav is not equal to the F_norm value. The normal force is provided in the problem statement. This 166-N normal force is the upward force exerted upon the bottom box; it serves as the force on the system since the bottom box is part of the system. The net force is the vector sum of these two forces. So

F_net = 166 N, up + 137.2 N, down = 28.8 N, up

The acceleration can be calculated using Newton's second law:

a = F_net /m = 28.8 N/14.0 kg = 2.0571 m/s² = ~2.1 m/s²

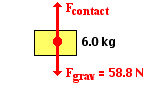Now that the system analysis has been used to determine the acceleration, an individual object analysis can be performed on either box in order to determine the force acting between them. As in the previous problems, it does not matter which box is chosen; the result will be the same in either case. The top box is used in this analysis since it encounters one less force. The free-body diagram is shown at the right. The force of gravity on the top box is m•g where m = 6.0 kg. The force of gravity is 58.8 N. The upward force is not known but can be calculated if the F_net = m•a equation is applied to the free-body diagram. Since the acceleration is upward, the Fnet side of the equation would be equal to the force in the direction of the acceleration (F_contact) minus the force that opposes it (F_grav). So

F_contact - 58.8 N = (6.0 kg)•(2.0571 m/s2)

(Notice that the unrounded value of acceleration is used here; rounding will occur when the final answer is determined.) Solving for F_contact yields 71.14 N. This figure can be rounded to two significant digits - 71 N. So the dual combination of the system analysis and the individual body analysis leads to an acceleration of 2.1 m/s² and a contact force of 71 N.

Now the second problem-solving approach will be used to solve the same problem. In this solution, two individual object analyses will be combined to generate a system of two equations capable of solving for the two unknowns. We will start this analysis by presuming that we are solving the problem for the first time and do not know the acceleration nor the contact force. The free-body diagrams for the individual objects are shown below.

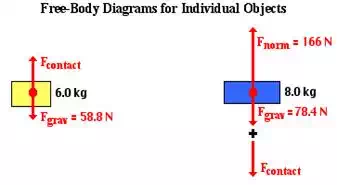
Note that the F_grav values for the two boxes have been included on the diagram. These were calculated using F_grav = m•g where m=6.0 kg for the top box and m=8.0 kg for the bottom box. The contact force (F_contact) on the top box is upward since the bottom box is pushing it upward as the system of two objects accelerates upward. The contact force (F_contact) on the bottom box is downward since the top box pushes downward on the bottom box as the acceleration occurs. These two contact forces are equal to one another since they result from a mutual interaction between the two boxes. The third force on the bottom box is the force of the scale pushing upward on it with 166 N of force; this value was given in the problem statement.

Applying Newton's second law to these two free-body diagrams leads to Equation 5 (for the 6.0-kg box) and Equation 6 (for the 8.0-kg box).

F_contact - 58.8 = 6.0 • a

166 - F_contact - 78.4 = 8.0 • a

Now that a system of two equations has been developed, algebra can be used to solve for the two unknowns. Equation 5 can be used to write an expression for the contact force (F_contact) in terms of the acceleration (a).

F_contact = 6.0 • a + 58.8

This expression for F_contact can then be substituted into equation 6. Equation 6 then becomes

166 - (6.0 • a + 58.8) - 78.4 = 8.0 • a

The following algebraic steps are performed on the above equation to solve for acceleration.

166 - 6.0 • a - 58.8 - 78.4 = 8.0 • a
166 - 58.8 - 78.4 = 8.0 • a + 6.0 • a
28.8 = 14.0 a
a = 2.0571 m/s² = ~2.1 m/s²

Now the value for acceleration (a) can be substituted back into the expression for F_contact (F_contact = 6.0 • a + 58.8) to solve for F_contact. The contact force is 71.14 N (~71 N).

It should be noted that the second approach to this problem yields the same numerical answers as the first approach. Students are encouraged to use the approach that they are most comfortable with.

For additional practice, consider the following two-body problems. A shortened version of the solution has been provided for each problem. The topic of two-body problems will be returned to in the next chapterwhen we consider situations involving pulleys and objects moving in different directions.

Check Your Understanding

1. A truck hauls a car cross-country. The truck's mass is 4.00x10³ kg and the car's mass is 1.60x10³ kg. If the force of propulsion resulting from the truck's turning wheels is 2.50x10⁴ N, then determine the acceleration of the car (or the truck) and the force at which the truck pulls upon the car. Assume negligible air resistance forces.

See Answer

a = 4.46 m/s² and F_truck-car = 7140 N (rounded from 7143 N)

The solution here will use the approach of a system analysis and an individual object analysis. The free-body diagrams for the system and for the car are shown below.

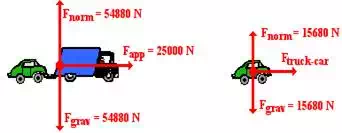
For the system: F_net = 2.50x10⁴ N and m_system = 5.60x10³ kg. So

a = F_net/m = (2.50x10⁴ N) / (5.60x10³ kg) = 4.4643 m/s²

For the individual object analysis on the car: m = 1.60x10³ kg and a = 4.46 m/s² (from above); so the F_net is m•a or 7143 N. This value of F_net is supplied by the force of the truck pulling the car.

close

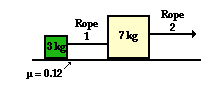2. A 7.00-kg box is attached to a 3.00-kg box by rope 1. The 7.00-kg box is pulled by rope 2 with a force of 25.0 N. Determine the acceleration of the boxes and the tension in rope 1. The coefficient of friction between the ground and the boxes is 0.120.

See Answer

a = 1.32 m/s² and F_rope 1 = 7.50 N

The solution here will use the approach of a system analysis and an individual object analysis .  The free-body diagrams for the system and for the 3-kg object are shown below.

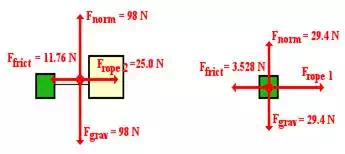
For the system: F_frict = μ•F_norm = 0.120• 98.0 N = 11.76 N

F_net = 25.0 N - 11.76 N = 13.24 N and m_system = 10.0 kg.

So a = F_net/m = (13.24 N) / (10.0 kg) = 1.324 m/s² (round to 1.32 m/s²)

For the individual object analysis on the 3.00-kg box: m = 3.00 kg and a = 1.324 m/s² (from above); so the F_net is m•a or 3.972 N.

This value of F_net is equal to the force in the direction of the acceleration (F_rope 1) minus the force that opposes it (F_frict).

For the 3.00-kg box, F_frict = μ•F_norm = 0.120• 29.4 N = 3.528 N.

So F_net = F_rope 1 - F_frict or

3.972 N = F_rope 1 - 3.528 N

Solving for F_rope 1 gives 7.50 N.

3. A tractor is being used to pull two large logs across a field. A chain connects the logs to each other; the front log is connected to the tractor by a separate chain. The mass of the front log is 180 kg. The mass of the back log is 220 kg. The coefficient of friction between the logs and the field is approximately 0.45. The tension in the chain connecting the tractor to the front log is 1850 N. Determine the acceleration of the logs and the tension in the chain that connects the two logs.

See Answer

a = 0.22 m/s² and F_rope 1 =1.0x10³ N

The solution here will use the approach of a system analysis and an individual object analysis . The free-body diagrams for the system and for the 220-kg rear log are shown below.

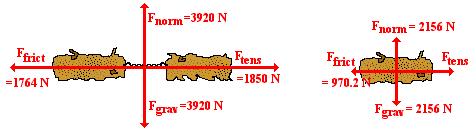
For the system: F_norm = F_grav = 400 kg • 9.8 N/kg = 3920 N
F_frict = μ•F_norm = 0.45 • 3920 N = 1764 N
F_net = 1850 N - 1764 N = 86 N and m_system = 400 kg. So

a = F_net/m = (86 N) / (400 kg) = 0.2150 m/s² = ~0.22 m/s²

For the individual object analysis on the 220-kg back log:
F_norm = F_grav = 220 kg • 9.8 N/kg = 2156 N
F_frict = μ•F_norm = 0.45 • 2156 N = 970.2 N
F_net = m•a = 220 kg • 0.2150 m/s² = 47.3 N

Applying Newton's second law: F_tens - 970.2 N = 47.3 N
So F_tens = 1017.5 N = ~1.0 x 10³ N

{^cosymantecnisbfw^}

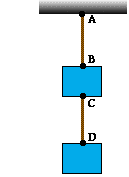4. Two boxes are held together by a strong wire and attached to the ceiling of an elevator by a second wire (see diagram). The mass of the top box is 14.2 kg; the mass of the bottom box is 10.4 kg. The elevator accelerates upwards at 2.84 m/s². (Assume the wire is relatively massless.)

(a) Find the tension in the top wire (connecting points A and B).

(b) Find the tension in the bottom wire (connecting points C and D).

See Answer

F_tens A-B = 311 N and F_tens C-D = 131 N

For the system: m_system = 10.4 kg + 14.2 kg = 24.6 kg
F_grav = 24.6 kg • 9.8 N/kg = 241.08 N
F_net = m_system • a = 24.6 kg • 2.84 m/s² = 69.864 N, upward

Applying Newton's second law to the system:
F_tens A-B - 241.08 N = 69.864 N
F_tens A-B = 310.944 N = ~311 N

For the individual object analysis on the 10.4-kg bottom box :
F_grav = 10.4 kg • 9.8 N/kg = 101.92 N
F_net = m•a = 10.4 kg • 2.84 m/s² = 29.536 N, upward

Applying Newton's second law to the 10.4-kg box:
F_tens C-D - 101.92 N = 29.536 N
F_tens C-D = 131.456 N = ~131 N