Falling with Air Resistance

As an object falls through air, it usually encounters some degree of air resistance. Air resistance is the result of collisions of the object's leading surface with air molecules. The actual amount of air resistance encountered by the object is dependent upon a variety of factors. To keep the topic simple, it can be said that the two most common factors that have a direct effect upon the amount of air resistance are the speed of the object and the cross-sectional area of the object. Increased speeds result in an increased amount of air resistance. Increased cross-sectional areas result in an increased amount of air resistance.

Why does an object that encounters air resistance eventually reach a terminal velocity? To answer this questions, Newton's second law will be applied to the motion of a falling skydiver.

In the diagrams below, free-body diagrams showing the forces acting upon an 85-kg skydiver (equipment included) are shown. For each case, use the diagrams to determine the net force and acceleration of the skydiver at each instant in time. Then use the button to view the answers.

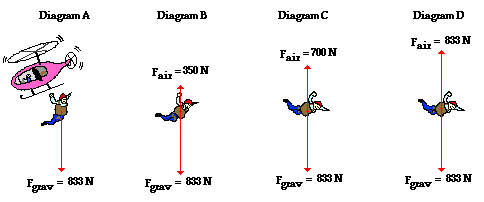
See Answer to A

The F_net = 833 N, down and the a = 9.8 m/s/s, down

a = (F_net / m) = (833 N) / (85 kg) = 9.8 m/s/s

See Answer to B

The F_net = 483 N, down and the a = 5.68 m/s/s, down

a = (F_net / m) = (483 N) / (85 kg) = 5.68 m/s/s

See Answer to C

The F_net = 133 N, down and the a = 1.56 m/s/s, down

a = (F_net / m) = (133 N) / (85 kg) = 1.56 m/s/s

See Answer to D

The F_net = 0 N and the a = 0 m/s/s

a = (F_net / m) = (0 N) / (85 kg) = 0 m/s/s.

The diagrams above illustrate a key principle. As an object falls, it picks up speed. The increase in speed leads to an increase in the amount of air resistance. Eventually, the force of air resistance becomes large enough to balances the force of gravity. At this instant in time, the net force is 0 Newton; the object will stop accelerating. The object is said to have reached a terminal velocity. The change in velocity terminates as a result of the balance of forces. The velocity at which this happens is called the terminal velocity.

In situations in which there is air resistance, more massive objects fall faster than less massive objects. But why? To answer the why question, it is necessary to consider the free-body diagrams for objects of different mass. Consider the falling motion of two skydivers: one with a mass of 100 kg (skydiver plus parachute) and the other with a mass of 150 kg (skydiver plus parachute). The free-body diagrams are shown below for the instant in time in which they have reached terminal velocity.

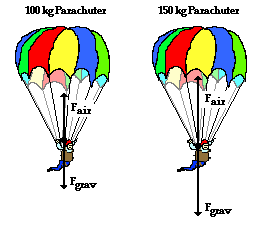
As learned above, the amount of air resistance depends upon the speed of the object. A falling object will continue to accelerate to higher speeds until they encounter an amount of air resistance that is equal to their weight. Since the 150-kg skydiver weighs more (experiences a greater force of gravity), it will accelerate to higher speeds before reaching a terminal velocity. Thus, more massive objects fall faster than less massive objects because they are acted upon by a larger force of gravity; for this reason, they accelerate to higher speeds until the air resistance force equals the gravity force.