Force is a Vector Quantity              

A force is a vector quantity. As learned in an earlier unit, a vector quantity is a quantity that has both magnitude and direction. To fully describe the force acting upon an object, you must describe both the magnitude (size or numerical value) and the direction. Thus, 10 Newton is not a full description of the force acting upon an object. In contrast, 10 Newton, downward is a complete description of the force acting upon an object; both the magnitude (10 Newton) and the direction (downward) are given.

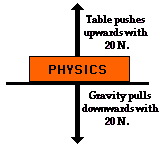Because a force is a vector that has a direction, it is common to represent forces using diagrams in which a force is represented by an arrow. Such vector diagrams were introduced in an earlier unit and are used throughout the study of physics. The size of the arrow is reflective of the magnitude of the force and the direction of the arrow reveals the direction that the force is acting. (Such diagrams are known as free-body diagrams and are discussed later in this lesson.) Furthermore, because forces are vectors, the effect of an individual force upon an object is often canceled by the effect of another force. For example, the effect of a 20-Newton upward force acting upon a book is canceled by the effect of a 20-Newton downward force acting upon the book. In such instances, it is said that the two individual forces balance each other; there would be no unbalanced force acting upon the book.

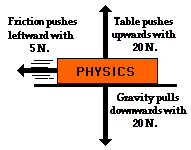Other situations could be imagined in which two of the individual vector forces cancel each other ("balance"), yet a third individual force exists that is not balanced by another force. For example, imagine a book sliding across the rough surface of a table from left to right. The downward force of gravity and the upward force of the table supporting the book act in opposite directions and thus balance each other. However, the force of friction acts leftwards, and there is no rightward force to balance it. In this case, an unbalanced force acts upon the book to change its state of motion.

The exact details of drawing free-body diagrams are discussed later. For now, the emphasis is upon the fact that a force is a vector quantity that has a direction. The importance of this fact will become clear as we analyze the individual forces acting upon an object later in this lesson.