Kinematic Equations and Graphs

· Kinematic Equations and Graphs

Lesson 4 of this unit at The Physics Classroom focused on the use of velocity-time graphs to describe the motion of objects. In that Lesson, it was emphasized that the slope of the line on a velocity-time graph is equal to the acceleration of the object and the area between the line and the time axis is equal to the displacement of the object. Thus, velocity-time graphs can be used to determine numerical values and relationships between the quantities displacement (d), velocity (v), acceleration (a) and time (t). In Lesson 6, the focus has been upon the use of four kinematic equations to describe the motion of objects and to predict the numerical values of one of the four motion parameters - displacement (d), velocity (v), acceleration (a) and time (t). Thus, there are now two methods available to solve problems involving the numerical relationships between displacement, velocity, acceleration and time. In this part of Lesson 6, we will investigate the relationships between these two methods.

Example Problem - Graphical Solution

Consider an object that moves with a constant velocity of +5 m/s for a time period of 5 seconds and then accelerates to a final velocity of +15 m/s over the next 5 seconds. Such a verbal description of motion can be represented by a velocity-time graph. The graph is shown below.

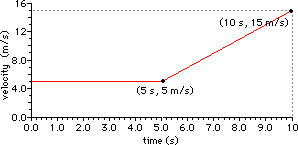
The horizontal section of the graph depicts a constant velocity motion, consistent with the verbal description. The positively sloped (i.e., upward sloped) section of the graph depicts a positive acceleration, consistent with the verbal description of an object moving in the positive direction and speeding up from 5 m/s to 15 m/s. The slope of the line can be computed using the rise over run ratio. Between 5 and 10 seconds, the line rises from 5 m/s to 15 m/s and runs from 5 s to 10 s. This is a total rise of +10 m/s and a total run of 5 s. Thus, the slope (rise/run ratio) is (10 m/s)/(5 s) = 2 m/s². Using the velocity-time graph, the acceleration of the object is determined to be 2 m/s² during the last five seconds of the object's motion.The displacement of the object can also be determined using the velocity-time graph. The area between the line on the graph and the time-axis is representative of the displacement; this area assumes the shape of a trapezoid. As discussed in Lesson 4, the area of a trapezoid can be equated to the area of a triangle lying on top of the area of a rectangle. This is illustrated in the diagram below.

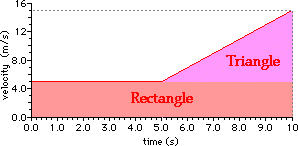
The total area is then the area of the rectangle plus the area of the triangle. The calculation of these areas is shown below.

Rectangle	Triangle
Area = base * height Area = (10 s) * (5 m/s) Area = 50 m	Area = 0.5 * base * height Area = 0.5 * (5 s) * (10 m/s) Area = 25 m

The total area (rectangle plus triangle) is equal to 75 m. Thus the displacement of the object is 75 meters during the 10 seconds of motion.

The above discussion illustrates how a graphical representation of an object's motion can be used to extract numerical information about the object's acceleration and displacement. Once constructed, the velocity-time graph can be used to determine the velocity of the object at any given instant during the 10 seconds of motion. For example, the velocity of the object at 7 seconds can be determined by reading the y-coordinate value at the x-coordinate of 7 s. Thus, velocity-time graphs can be used to reveal (or determine) numerical values and relationships between the quantities displacement (d), velocity (v), acceleration (a) and time (t) for any given motion.

Example Problem - Solution Using Kinematic Equation

Now let's consider the same verbal description and the corresponding analysis using kinematic equations. The verbal description of the motion was:

An object that moves with a constant velocity of +5 m/s for a time period of 5 seconds and then accelerates to a final velocity of +15 m/s over the next 5 seconds

Kinematic equations can be applied to any motion for which the acceleration is constant. Since this motion has two separate acceleration stages, any kinematic analysis requires that the motion parameters for the first 5 seconds not be mixed with the motion parameters for the last 5 seconds. The table below lists the given motion parameters.

t = 0 s - 5 s	t = 5 s - 10 s
vi = 5 m/s vf = 5 m/s t = 5 s a = 0 m/s^2	vi = 5 m/s vf = 15 m/s t = 5 s

Note that the acceleration during the first 5 seconds is listed as 0 m/s² despite the fact that it is not explicitly stated. The phrase constant velocity indicates a motion with a 0 acceleration. The acceleration of the object during the last 5 seconds can be calculated using the following kinematic equation.

v_f = v_i + a*t

The substitution and algebra are shown here.

15 m/s = 5 m/s + a*(5 s)
15 m/s - 5 m/s = a*(5 s)

10 m/s = a*(5 s)

(10 m/s)/(5 s) = a

a = 2 m/s²

This value for the acceleration of the object during the time from 5 s to 10 s is consistent with the value determined from the slope of the line on the velocity-time graph.

The displacement of the object during the entire 10 seconds can also be calculated using kinematic equations. Since these 10 seconds include two distinctly different acceleration intervals, the calculations for each interval must be done separately. This is shown below.

t = 0 s - 5 s	t = 5 s - 10 s
d = vi*t + 0.5*a*t^2 d = (5 m/s)*(5 s) +0.5*(0 m/s^2)*(5 s)^2 d = 25 m + 0 m d = 25 m	d = ((vi + vf)/2)*t d = ((5 m/s + 15 m/s)/2)*(5 s) d = (10 m/s)*(5 s) d = 50 m

The total displacement during the first 10 seconds of motion is 75 meters, consistent with the value determined from the area under the line on the velocity-time graph.

The analysis of this simple motion illustrates the value of these two representations of motion - velocity-time graph and kinematic equations. Each representation can be utilized to extract numerical information about unknown motion quantities for any given motion. The examples below provide useful opportunity for those requiring additional practice.

Check Your Understanding

1. Rennata Gas is driving through town at 25.0 m/s and begins to accelerate at a constant rate of -1.0 m/s². Eventually Rennata comes to a complete stop.

a. Represent Rennata's accelerated motion by sketching a velocity-time graph. Use the velocity-time graph to determine this distance.
b. Use kinematic equations to calculate the distance that Rennata travels while decelerating.

2. Otto Emissions is driving his car at 25.0 m/s. Otto accelerates at 2.0 m/s² for 5 seconds. Otto then maintains a constant velocity for 10.0 more seconds.

a. Represent the 15 seconds of Otto Emission's motion by sketching a velocity-time graph. Use the graph to determine the distance that Otto traveled during the entire 15 seconds.
b. Finally, break the motion into its two segments and use kinematic equations to calculate the total distance traveled during the entire 15 seconds.

3. Luke Autbeloe, a human cannonball artist, is shot off the edge of a cliff with an initial upward velocity of +40.0 m/s. Luke accelerates with a constant downward acceleration of -10.0 m/s² (an approximate value of the acceleration of gravity).

a. Sketch a velocity-time graph for the first 8 seconds of Luke's motion.
b. Use kinematic equations to determine the time required for Luke Autbeloe to drop back to the original height of the cliff. Indicate this time on the graph.

4. Chuck Wagon travels with a constant velocity of 0.5 mile/minute for 10 minutes. Chuck then decelerates at -.25 mile/min² for 2 minutes.

a. Sketch a velocity-time graph for Chuck Wagon's motion. Use the velocity-time graph to determine the total distance traveled by Chuck Wagon during the 12 minutes of motion.
b. Finally, break the motion into its two segments and use kinematic equations to determine the total distance traveled by Chuck Wagon.

5. Vera Side is speeding down the interstate at 45.0 m/s. Vera looks ahead and observes an accident that results in a pileup in the middle of the road. By the time Vera slams on the breaks, she is 50.0 m from the pileup. She slows down at a rate of -10.0 m/s².

a. Construct a velocity-time plot for Vera Side's motion. Use the plot to determine the distance that Vera would travel prior to reaching a complete stop (if she did not collide with the pileup).
b. Use kinematic equations to determine the distance that Vera Side would travel prior to reaching a complete stop (if she did not collide with the pileup). Will Vera hit the cars in the pileup? That is, will Vera travel more than 50.0 meters?

6. Earl E. Bird travels 30.0 m/s for 10.0 seconds. He then accelerates at 3.00 m/s² for 5.00 seconds.

a.Construct a velocity-time graph for Earl E. Bird's motion. Use the plot to determine the total distance traveled.
b. Divide the motion of the Earl E. Bird into the two time segments and use kinematic equations to calculate the total displacement.

Solutions to Above Questions

Solution to Question 1

a. The velocity-time graph for the motion is:

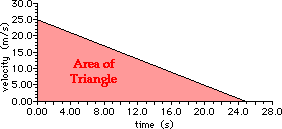
The distance traveled can be found by a calculation of the area between the line on the graph and the time axis.

Area = 0.5*b*h = 0.5*(25.0 s)*(25.0 m/s)

Area = 313 m

b. The distance traveled can be calculated using a kinematic equation. The solution is shown here.

Given:

vi = 25.0 m/s

vf = 0.0 m/s

a = -1.0 m/s^2

Find:

d = ??

v_f² = v_i² + 2*a*d

(0 m/s)² = (25.0 m/s)² + 2 * (-1.0 m/s²)*d

0.0 m²/s² = 625.0 m²/s² + (-2.0 m/s²)*d

0.0 m²/s² - 625.0 m²/s² = (-2.0 m/s²)*d

(-625.0 m²/s²)/(-2.0 m/s²) = d

313 m = d

Solution to Question 2

a. The velocity-time graph for the motion is:

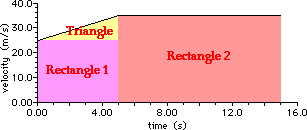
The distance traveled can be found by a calculation of the area between the line on the graph and the time axis. This area would be the area of the triangle plus the area of rectangle 1 plus the area of rectangle 2.

Area = 0.5*b_tri*h_tri + b_rect1*h_rect1 + b_rect2*h_rect2

Area = 0.5*(5.0 s)*(10.0 m/s) + (5.0 s)*(25.0 m/s) + (10.0 s)*(35.0 m/s)

Area = 25 m + 125 m + 350 m

Area = 500 m

b. The distance traveled can be calculated using a kinematic equation. The solution is shown here.

First find the d for the first 5 seconds:

Given:

vi = 25.0 m/s

t = 5.0 s

a = 2.0 m/s^2

Find:

d = ??

d = v_i*t + 0.5*a*t²

d = (25.0 m/s)*(5.0 s) + 0.5*(2.0 m/s²)*(5.0 s)²

d = 125 m + 25.0 m

d = 150 m

Now find the d for the last 10 seconds:

Given:

vi = 35.0 m/s

t = 10.0 s

a = 0.0 m/s^2

Find:

d = ??

(Note: the velocity at the 5 second mark can be found from knowing that the car accelerates from 25.0 m/s at +2.0 m/s² for 5 seconds. This results in a velocity change of a*t = 10 m/s, and thus a velocity of 35.0 m/s.)

d = v_i*t + 0.5*a*t²

d = (35.0 m/s)*(10.0 s) + 0.5*(0.0 m/s²)*(10.0 s)²

d = 350 m + 0 m

d =350 m

The total distance for the 15 seconds of motion is the sum of these two distance calculations (150 m + 350 m):

distance = 500 m

Solution to Question 3

a. The velocity-time graph for the motion is:

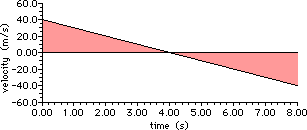
b. The time to rise up and fall back down to the original height is twice the time to rise up to the peak. So the solution involves finding the time to rise up to the peak and then doubling it.

Given:

vi = 40.0 m/s

vf = 0.0 m/s

a = -10.0 m/s^2

Find:

t_up = ??

2*t_up = ??

v_f = v_i + a*t_up

0 m/s = 40 m/s + (-10 m/s2)*t_up

(10 m/s²)*t_up = 40 m/s

t_up = (40 m/s)/(10 m/s²)

t_up = 4.0 s

2*t_up = 8.0 s

Solution to Question 4

a. The velocity-time graph for the motion is:

The distance traveled can be found by a calculation of the area between the line on the graph and the time axis. This area would be the area of the rectangle plus the area of the triangle.

Area = b_rect*h_rect + 0.5*b_tri*h_tri

Area = (10.0 min)*(0.50 mi/min) + 0.5*(2.0 min)*(0.50 mi/min)

Area = 5 mi + 0.5 mi

Area = 5.5 mi

b. The distance traveled can be calculated using a kinematic equation. The solution is shown here.

First find the d for the first 10 minutes:

Given:

vi = 0.50 mi/min

t = 10.0 min

a = 0.0 mi/min^2

Find:

d = ??

d = v_i*t + 0.5*a*t²

d = (0.50 mi/min)*(10.0 min) + 0.5*(0.0 mi/min²)*(10.0 min)²

d = 5.0 mi + 0 mi

d = 5.0 mi

Now find the d for the last 2 minutes:

Given:

vi = 0.50 mi/min

t = 2.0 min

a = -0.25 mi/min^2

Find:

d = ??

d = v_i*t + 0.5*a*t²

d = (0.50 mi/min)*(2.0 min) + 0.5*(-0.25 m/s²)*(2.0 min)²

d = 1.0 mi + (-0.5 mi)

d = 0.5 mi

The total distance for the 12 minutes of motion is the sum of these two distance calculations (5.0 mi + 0.5 mi):

distance = 5.5 mi

Solution to Question 5

a. The velocity-time graph for the motion is:

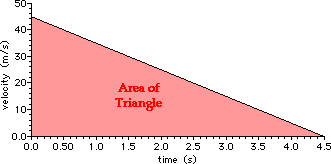
The distance traveled can be found by a calculation of the area between the line on the graph and the time axis.

Area = 0.5*b*h = 0.5*(4.5 s)*(45.0 m/s)

Area = 101 m

b.

Given:

vi = 45.0 m/s

vf = 0.0 m/s

a = -10.0 m/s^2

Find:

d = ??

v_f² = v_i² + 2*a*d

(0 m/s)² = (45.0 m/s)² + 2 * (-10.0 m/s²)*d

0.0 m²/s² = 2025.0 m²/s² + (-20.0 m/s²)*d

0.0 m²/s² - 2025.0 m²/s² = (-20.0 m/s²)*d

(-2025.0 m²/s²)/(-20.0 m/s²) =d

101 m =d

Since the accident pileup is less than 101 m from Vera, she will indeed hit the pileup before completely stopping (unless she veers aside).

Solution to Question 6

a. The velocity-time graph for the motion is:

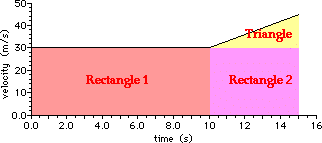
The distance traveled can be found by a calculation of the area between the line on the graph and the time axis. This area would be the area of the triangle plus the area of rectangle 1 plus the area of rectangle 2.

Area = 0.5*b_tri*h_tri + b₁*h₁ + b₂*h₂

Area = 0.5*(5.0 s)*(15.0 m/s) + (10.0 s)*(30.0 m/s) + (5.0 s)*(30.0 m/s)

Area = 37.5 m + 300 m + 150 m

Area = 488 m

b. The distance traveled can be calculated using a kinematic equation. The solution is shown here.

First find the d for the first 10 seconds:

Given:

vi = 30.0 m/s

t = 10.0 s

a = 0.0 m/s^2

Find:

d = ??

d = v_i*t + 0.5*a*t²

d = (30.0 m/s)*(10.0 s) + 0.5*(0.0 m/s²)*(10.0 s)²

d = 300 m + 0 m

d =300 m

Now find the d for the last 5 seconds:

Given:

vi = 30.0 m/s

t = 5.0 s

a = 3.0 m/s^2

Find:

d = ??

d = v_i*t + 0.5*a*t²

d = (30.0 m/s)*(5.0 s) + 0.5*(3.0 m/s²)*(5.0 s)²

d = 150 m + 37.5 m

d = 187.5 m

The total distance for the 15 seconds of motion is the sum of these two distance calculations (300 m + 187.5 m):

distance = 488 m