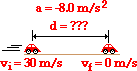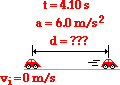Kinematic Equations and Problem-Solving
The four kinematic equations that describe the mathematical
relationship between the parameters that describe an object's motion were
introduced in the previous part of Lesson 6. The four kinematic
equations are:
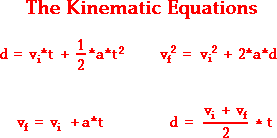
In the above equations, the symbol d stands for the displacement of the object. The symbol t stands for thetime for which
the object moved. The symbol a stands for
the acceleration of the
object. And the symbol vstands for
the instantaneous velocity of the object; a subscript of i after the v
(as in vi) indicates that the velocity value is the initial velocity value and a subscript of f (as in vf) indicates that the velocity
value is thefinal velocity value.
Problem-Solving
Strategy
In this part of Lesson 6 we will investigate the process of
using the equations to determine unknown information about an object's motion.
The process involves the use of a problem-solving strategy that will be used
throughout the course. The strategy involves the following steps:
1. Construct
an informative diagram of the physical situation.
2. Identify
and list the given information in variable form.
3. Identify
and list the unknown information in variable form.
4. Identify
and list the equation that will be used to determine unknown information from
known information.
5. Substitute
known values into the equation and use appropriate algebraic steps to solve for
the unknown information.
6. Check your
answer to insure that it is reasonable and mathematically correct.
The use of this problem-solving strategy in the solution of
the following problem is modeled in Examples A and B below.
Example
Problem A
Ima Hurryin is approaching a stoplight moving with a velocity of +30.0 m/s.
The light turns yellow, and Ima applies the brakes and skids to a stop. If
Ima's acceleration is -8.00 m/s2, then determine the displacement of
the car during the skidding process. (Note that the direction of the velocity
and the acceleration vectors are denoted by a + and a - sign.)
The solution to this problem begins by the construction of an
informative diagram of the physical situation. This is shown below. The second
step involves the identification and listing of known information in variable
form. Note that the vf value can
be inferred to be 0 m/s since Ima's car comes to a stop. The initial velocity (vi) of the
car is +30.0 m/s since this is the velocity at the beginning of the motion (the
skidding motion). And the acceleration (a) of the car is given as - 8.00 m/s2.
(Always pay careful attention to the + and - signs for the given quantities.)
The next step of the strategy involves
the listing of the unknown (or desired) information in variable form. In this
case, the problem requests information about the displacement of the car. So d is the unknown quantity. The results of the first three steps are shown
in the table below.
|
Diagram: |
Given: |
Find: |
|
|
vi = +30.0 m/s |
d = ?? |
The next step of the strategy involves
identifying a kinematic equation that would allow you to determine the unknown
quantity. There are four kinematic equations to choose from. In general, you
will always choose the equation that contains the three known and the one
unknown variable. In this specific case, the three known variables and the one
unknown variable are vf, vi, a, and d. Thus, you will look for an equation that has these four variables
listed in it. An inspection of the four equations above reveals
that the equation on the top right contains all four variables.
vf2 = vi2 + 2 • a • d
Once the equation is identified and written down, the next
step of the strategy involves substituting known values into the equation and using proper
algebraic steps to solve for the unknown information. This step is shown below.
(0 m/s)2 = (30.0 m/s)2 + 2 • (-8.00 m/s2)
• d
0 m2/s2 = 900 m2/s2 + (-16.0 m/s2)
• d
(16.0 m/s2) • d = 900 m2/s2 - 0 m2/s2
(16.0 m/s2)*d = 900 m2/s2
d = (900 m2/s2)/ (16.0 m/s2)
d = (900 m2/s2)/ (16.0 m/s2)
d = 56.3 m
The solution above reveals that the car will skid a distance
of 56.3 meters. (Note that this value is rounded to the third digit.)
The last step of the problem-solving strategy involves
checking the answer to assure that it is both reasonable and accurate. The
value seems reasonable enough. It takes a car a considerable distance to skid
from 30.0 m/s (approximately 65 mi/hr) to a stop. The calculated distance is
approximately one-half a football field, making this a very reasonable skidding
distance. Checking for accuracy involves substituting the calculated value back
into the equation for displacement and insuring that the left side of the
equation is equal to the right side of the equation. Indeed it is!
Example
Problem B
Ben Rushin is waiting at a stoplight. When it finally turns green, Ben
accelerated from rest at a rate of a 6.00 m/s2 for a time of 4.10 seconds. Determine the displacement of Ben's car
during this time period.
Once more, the solution to this problem begins by the
construction of an informative diagram of the physical situation. This is shown
below. The second step of the strategy involves
the identification and listing of known information in variable form. Note that
the vi value can
be inferred to be 0 m/s since Ben's car is initially at rest. The acceleration
(a) of the car is
6.00 m/s2. And the time (t) is given as 4.10 s. The next step of the strategy involves
the listing of the unknown (or desired) information in variable form. In this
case, the problem requests information about the displacement of the car. So d is the unknown information. The results of the first three steps are
shown in the table below.
|
Diagram: |
Given: |
Find: |
|
|
vi = 0 m/s |
d = ?? |
The next step of the strategy involves
identifying a kinematic equation that would allow you to determine the unknown
quantity. There are four kinematic equations to choose from. Again, you will
always search for an equation that contains the three known variables and the
one unknown variable. In this specific case, the three known variables and the
one unknown variable are t, vi, a, and
d. An inspection of the four equations above reveals
that the equation on the top left contains all four variables.
d = vi • t + ½ • a • t2
Once the equation is identified and written down, the next step of the strategy involves
substituting known values into the equation and using proper algebraic steps to
solve for the unknown information. This step is shown below.
d = (0 m/s) • (4.1 s) + ½ • (6.00 m/s2) • (4.10 s)2
d = (0 m) + ½ • (6.00 m/s2) • (16.81 s2)
d = 0 m + 50.43 m
d = 50.4 m
The solution above reveals that the car will travel a
distance of 50.4 meters. (Note that this value is rounded to the third digit.)
The last step of the problem-solving strategy involves
checking the answer to assure that it is both reasonable and accurate. The
value seems reasonable enough. A car with an acceleration of 6.00 m/s/s will
reach a speed of approximately 24 m/s (approximately 50 mi/hr) in 4.10 s. The
distance over which such a car would be displaced during this time period would
be approximately one-half a football field, making this a very reasonable
distance. Checking for accuracy involves substituting the calculated value back
into the equation for displacement and insuring that the left side of the
equation is equal to the right side of the equation. Indeed it is!
The two example problems above illustrate how the kinematic
equations can be combined with a simpleproblem-solving strategy to predict
unknown motion parameters for a moving object. Provided that three motion
parameters are known, any of the remaining values can be determined. In the next part
of Lesson 6, we will see how this strategy can be applied to free fall
situations. Or if interested, you can try somepractice problems and check
your answer against the given solutions.