Determining
the Area on a v-t Graph
As learned in an earlier part of this lesson, a plot of
velocity-time can be used to determine the acceleration of an object (the
slope). In this part of the lesson, we will learn how a plot of velocity versus
time can also be used to determine the displacement of an object. For velocity
versus time graphs, the area bound by the line and the axes represents the
displacement. The diagram below shows three different velocity-time graphs; the
shaded regions between the line and the time-axis represent the displacement
during the stated time interval.
|
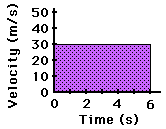
The
shaded area is representative of the displacement during from 0 seconds to 6 seconds. This area takes on
the shape of a rectangle can
be calculated using the appropriate equation. |
|
|
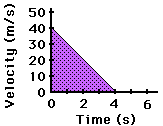
The shaded area is representative of
the displacement during from 0 seconds to 4 seconds. This area takes on the
shape of a triangle can
be calculated using the appropriate equation. |
|
|
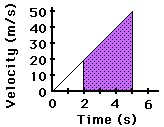
The shaded area is representative of
the displacement during from 2 seconds to 5 seconds. This area takes on the
shape of a trapezoid can be calculated using the
appropriate equation. |
|
The method used to find the area under a line on a
velocity-time graph depends upon whether the section bound by the line and the
axes is a rectangle, a triangle or a trapezoid. Area formulas for each shape
are given below.
|
Rectangle |
Triangle |
Trapezoid |
|
Area = b • h |
Area = ½ • b • h |
Area
= ½ • b • (h1 + h2) |
Calculating
the Area of a Rectangle
Now we will look at a few example computations of the area
for each of the above geometric shapes. First consider the calculation of the
area for a few rectangles. The solution for finding the area is shown for the
first example below. The shaded rectangle on the velocity-time graph has a base
of 6 s and a height of 30 m/s. Since the area of a rectangle is found by using
the formula A = b x h, the area is 180 m (6 s x 30 m/s). That is, the object
was displaced 180 meters during the first 6 seconds of motion.
|
|
Area = b * h |
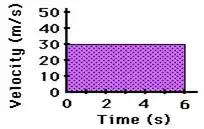
Now try the following two practice problems as a check of your
understanding. Determine the displacement (i.e., the area) of the object during
the first 4 seconds (Practice A) and from 3 to 6 seconds (Practice B).
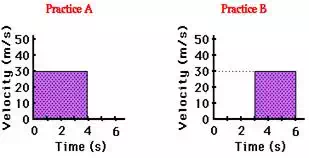
The area of a rectangle is determined by multiplying the base by
the height.
A = b • h where
b = 4 s and h = 30 m/s.
A = (4 s) • (30
m/s) = 120
m
That is, the
object was displaced 120 m during the first 4 seconds of motion.
The area of a rectangle is determined by multiplying the base by
the height.
A = b • h where
b = 3 s and h = 30 m/s.
A = (3 s) • (30
m/s) = 90 m
That is, the
object was displaced 90 m during the interval of time between 3 and 6 seconds.