Using the Slope Equation

The slope equation says that the slope of a line is found by determining the amount of rise of the line between any two points divided by the amount of run of the line between the same two points. In other words,

·         Pick two points on the line and determine their coordinates.

·         Determine the difference in y-coordinates of these two points (rise).

·         Determine the difference in x-coordinates for these two points (run).

·         Divide the difference in y-coordinates by the difference in x-coordinates (rise/run or slope).

The diagram below shows this method being applied to determine the slope of the line. Note that three different calculations are performed for three different sets of two points on the line. In each case, the result is the same: the slope is 10 m/s.

http://www.physicsclassroom.com/Class/1DKin/U1L3c3.webp

So that was easy - rise over run is all that is involved.

Now let's attempt a more difficult example. Consider the graph below. Note that the slope is not positive but rather negative; that is, the line slopes in the downward direction. Note also that the line on the graph does not pass through the origin. Slope calculations are relatively easy when the line passes through the origin since one of the points is (0,0). But that is not the case here. Test your understanding of slope calculations by determining the slope of the line below. Then click the button to check your answer.

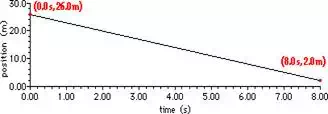
http://www.physicsclassroom.com/Class/1DKin/U1L3c5.webp


Check your understanding answer

Slope = -3.0 m/s

Using the two given data points, the rise can be calculated as -24.0 m (the - sign indicates a drop). The run can be calculated as 8.0 seconds. Thus, the slope is -3.0 m/s.

                                                        



 

Check Your Understanding

1. Determine the velocity (i.e., slope) of the object as portrayed by the graph below. When you believe you know the answer (and not before), click the button to check it.

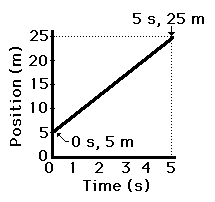
http://www.physicsclassroom.com/Class/1DKin/U1L3c4.webp


Check your understanding answer

The velocity (i.e., slope) is 4 m/s. If you think the slope is 5 m/s, then you're making a common mistake. You are picking one point (probably 5 s, 25 m) and dividing y/x. Instead you must pick two points (as discussed in this part of the lesson) and divide the change in y by the change in x.