Optical Rotation
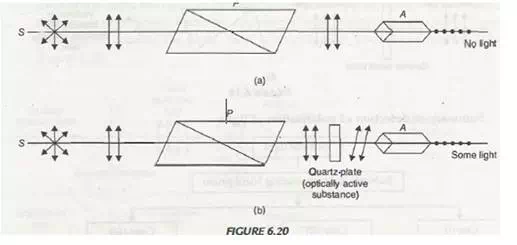
When a plane poiarised light is passed through certain substance, the plane of polarisation of the emergent light get rotated through certain angle about the direction of propagation of light. This phenomenon is called ‘Optical rotation’ or ‘Optical activity’ and the substance which rotates plane of polarized light are called optically active medium e.g., Sugar solution, turpentine, sodium chlorate, cinnabar etc.
The optically· active substances are of two types:
· Dextra rotatory or right handed.
· Laevo rotatory or left handed.
(i) Dextro rotatory or right handed. The substance which rotates plane of polarization of light towards right or in clockwise Direction are called dextro rotatory or right handed.
(ii) Laevo rotatory or left handed. The substance which rotates plane of polarization of light towards left or in anti-clockwise directions are called laevo rotatory or left handed.
Fresnel’s Theory of Optical Rotation
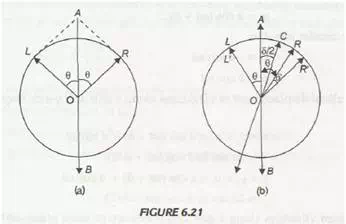
According to Fresnel’s a linearly plane polarised light can be supposed to be consists of two circularly polarised vibrations rotating in opposite directions. When a plane polarised light enters a crystal of calcite (which is optically inactive substance) along optical axis, it is resolved into two circularly polarised vibration rotating in opposite direction with same angular frequency or velocity such that resultant of these two vibrations at all point of time is along the optic axis. Vibrations rotating in clockwise (in Figure 6.21 (a)), direction are represented by OR and vibration rotating in anticlockwise direction are represented by OL ·The resultant OR and OL at all point of time will be along AB. In case of Quartz (which is optically active), a linearly polarised light on entering the crystal is resolved into two circularly polarised vibrations rotating in opposite direction with different angular velocity or frequency. In case of left handed optically active quartz crystal, anticlockwise vibrations travel faster, while in case of right handed optically active, quartz crystal, clockwise vibrations travel faster
Consider a right handed quartz crystal in which clockwise component travels faster than Left handed component. Suppose at any instant of time, right handed component traverse angle δ greater than left handed component as shown in Figure 6.21 (b). The new position of resultant of L’ and OR’ will be along CD i.e., plane of vibration of light has been rotated through angle δ/2 towards right after passing through quartz crystal. The angle δ/2 depends upon thickness of crystal
Mathematically,
(a) For calcite crystal which is optically inactive: when linearly plane polarised light enters a calcite crystal it get resolved into two circularly polarised vibrations. One is moving nticlockwise with same angular frequency or velocity. As each circularly polarised vibration further consist of two rectangular components having phase differences n/2, so,
for clockwise circular vibration
x1 =a sinθ =a sin wt
x2 =a cos θ =a cos wt
for clockwise circular vibration
x2 =-a sinθ =- a sin wt
y2 =a cos θ =a cos wt
From above, the resultant displacement of vibrations along x-axis and y-axis respectively
are given as,
x =x1+x2 =a sin θ – a sin θ =0
y =y1+y2 =a cos wt +a cos wt =2 a cos wt
Hence resultant vibration has amplitude 2a and is plane y-axis i.e., along original direction AB. Hence two oppositely circularly polarised vibrations give rise to a plane polarised
vibrations.
(b) For quartz crystal which is optically active: When linearly plane polarised light enters quartz crystal (right handed), it gets resolved into circularly polarised vibrations moving in opposite direction with different angular frequency or velocity. In case of right handed crystal clockwise vibrations travel faster than anticlockwise vibrations. Let at any instant of time anticlockwise vibrations has traversed angle e and clockwise vibrations has traversed angle ( θ+ δ). Therefore, component of two circular vibrations at that instant of time will be,
for clockwise vibration
x1 = a sin (wt + δ)
y1 = a cos (wt + δ)
for anticlockwise circular vibration
x2 = – a sin wt
y2 = a cos wt
From resultant displacement of vibrations along x-axis and y-axis respectively are given as,
x = x1 +x2 =a sin (wt =δ ) –a sin wt
=2a sin δ /2 cos (wt +δ/2)
Y = y1 +y2 =a cos (et +δ) +a cos wt
= 2a cos δ/2 cos (et +δ /2)
The resultant vibration along x-axis and y-axis are in same phase, so resultant of these vibrations is plane polarised and makes an angle of 8/2 with original direction AB. Thus, plane of vibrations get rotated through angle 8/2 towards right after passing through a right handed quartz crystal.
From above, we get
tan δ/2 = y/x ·
Angle of Rotation
If µR ,µL be the refractive indices of quartz crystal for right handed and left handed vibrations respectively, then optical path difference on passing through a quartz crystal slab of thickness ‘t’ is given as,
Path difference =(µL-µR) t
If λ be the wavelength of light used, then phase difference,
δ = 2π/λ (µL -µR)t.
Angle of rotation
δ/2 = π/λ(µL -µR)t
Specific Rotation
When a linearly plane polarised light is passed through an optically active medium/ substance, the plane of linearly polarised light get rotated through certain angle either towards left or right. The angle through which plane polarised light get rotated depends upon
(i) thickness of the medium
(ii) density of active substance or concentration of solution
(iii) Wavelength of light
(iv) Temperature.
The rotation produced by 1 decimeter (A. = 10 cm) long solution of concentration 1 gm/c at given temperature for given wavelength is known as specific rotation and given as,
[S]tλ =10θ/LC
Where θ = rotation in degree, L = length of tube in ems
C = concentration of solution in gm/ cc
t = temperature and λ. = wavelength of linearly polarised light
The rotation produced by optically active/medium/substance can be measured by polarimeter.