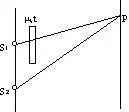
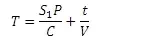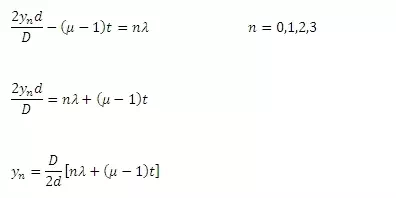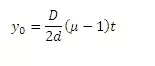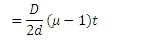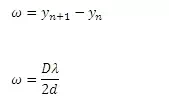Displacement of Fringes
When a film of thickness’t’ and refractive index 'm' is
introduced in the path of one of the sources, then fringe shift occurs as the
optical path difference changes.
Optical path difference at
P = S2P - [S1P+ µt - t] = S2P - S1P - (µ - 1)t = y.d/D - (µ - 1)
⇒ nth fringe is shifted by Δy = D(µ-1)t/d = w/λ (µ-1)t
Illustration:
Monochromatic light of wavelength of 600 nm is used in a YDSE. One of the slits is covered by a transparent sheet of thickness 1.8 x 10-5 m made of a material of refractive index 1.6. How many fringes will shift due to the introduction of the sheet?
Solution:
As derived earlier, the total fringe shift = w/λ (µ-1)t .
As each fringe width = w,
The number of fringes that will shift = total fringe shift/fring width
(w/λ(µ-1)t)/w = (µ-1)t/λ
= (1.6-1) x 1.8 x 10-5m / 600 x 10-9 = 18
Illustration:
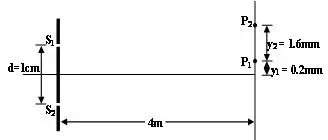
In the YDSE conducted with white light (4000Å-7000Å), consider two points P1 and P2 on the screen at y1=0.2mm and y2=1.6mm, respectively. Determine the wavelengths which form maxima at these points.
Solution:
The optical path difference at P1 is
p1 =dy1/d = ( 10/4000) (0.2) = 5 x 10-4mm = 5000Å
In the visible range 4000 - 7000Å
n1 = 5000/4000 = 1.25 and n2 = 5000/7000 = 0.714
The only integer between 0.714 and 1.25 is 1
∴ The wavelength which forms maxima at P is l = 5000Å
For the point P2,
p2 = dy2/D = ( 10/4000) (1.6) = 4 x 10-3mm = 40000Å
Here n1 = 40000/4000 = 10 and n2 = 40000/7000 = 5.71
The integers between 5.71 and 10 are 6, 7, 8, 9 and 10
∴The wavelengths which form maxima at P2 are
λ1 = 4000 Å for n = 10
λ2 = 4444 Å for n = 9
λ3 = 5000 Å for n = 8
λ4 = 5714 Å for n = 7
λ5 = 6666 Å for n = 6
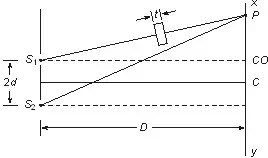
If a thin glass or mica strip or any other transparent plate of uniform thickness is introduced in the path of one of the two interfering beam from two coherent sources then central bright fringe will be displaced. This displacement from C to C00 will towards the side of lamina.
In order to calculate the displace we shall find the path difference between two beam from coherent sources S1 and S2 at any point ‘P’ on the screen. Let ‘t’ be the thickness of sheet and ‘μ’ the refractive index of its materials.
Time T taken by the beam to reach from S1 to P is given by
where C is the velocity in air and V is velocity of light in the medium of the plate

The condition for maxima
If P is the centre of the nth bright fringe
Shift of Central Fringe
Shift of central bright fringe where n=0 is given by
This expression is independent of n. This indicate that all the bright fringes are displaced through the same amount equal to similarly it can be shown that the displacement of any dark fringe is also
The fringe width ω is given by